Алгебра 10-11

Делимость чисел

Теория вероятностей

Задача. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.

Тригонометрия

Тригонометрические уравнения на ЕГЭ

Логарифмическая функция

Решите неравенство lg⁴(x² – 26)⁴ – 4lg²(x² – 26)² ≤ 240.

Производная

Производная. Часть 1

Пример. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

Пример. Написать уравнение касательной к графику функции у = -2х²-12х-13 в точке с абсциссой х₀ = -4. Сделать рисунок.

Пример. (Задача 6 ЕГЭ) Материальная точка движется прямолинейно по закону x(t) = t³ + 4t² -3t + 15, где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 7 с.

Экономические задачи ЕГЭ

Что необходимо понимать прежде, чем решать задачи на проценты и кредиты ЕГЭ по математике. Попробуем разобраться с механизмом кредитования населения. Итак, пусть банк выдал кредит в сумме S рублей под r%…

Задача. 15 января планируется взять кредит в банке на 19 месяцев. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Задача. 15 января планируется взять кредит в банке на 25 месяцев. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 13% больше, чем сумма, взятая в кредит. Найдите r%.

Задача. 15 января планируется взять кредит в банке на сумму 1,8 млн рублей на 24 месяца. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Какую сумму нужно вернуть банку в течение первого года кредитования?

Задача. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы: каждый январь долг возрастает на r% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший – не менее 0,6 млн рублей.

Задача. 15 января планируется взять кредит в банке на 21 месяц. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?

Задача. 15 января планируется взять кредит в банке на 2 года. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что за 15-й месяц кредитования нужно выплатить 44 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?

Задача. 15 января планируется взять кредит в банке на 3 года. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?

Задача. 15 января планируется взять кредит в банке на 24 месяца. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что в течение первого года кредитования нужно вернуть банку 466,5 тыс. рублей. Какую сумму планируется взять в кредит?

Задача. 15 января планируется взять кредит в банке на 24 месяца. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?

Задача. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Задача. 31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?

Задача. 31 декабря 2014 года Арсений взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определенное число процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?

Задача. В начале 2001 года Алексей приобрел ценную бумагу за 11000 рублей. В конце каждого года цена бумаги возрастает на 4000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Задача. Цена ценной бумаги на конец года вычисляется по формуле S=1,1S_o + 2000, где S_o – цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12 %. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тыс. рублей, которые он может положить на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.

Задача. В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы: в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года; в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18 % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2033 года кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?

Задача. В июле 2023 года планируется взять кредит в банке на 10 лет. Условия его возврата таковы: каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года; каждый январь с 2029 по 2033 год долг возрастает на 16 % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2033 года кредит должен быть полностью погашен. Найдите сумму, которую планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей.

Задача. В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы: в январе 2026, 2027 и 2028 годов долг возрастает на 20% по сравнению с концом предыдущего года; в январе 2029, 2030 и 2031 годов долг возрастает на r % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2031 года кредит должен быть полностью погашен. Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.

Задача. В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей. Условия его возврата таковы: каждый январь долг будет возрастать на 15% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо оплатить одним платежом часть долга; в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года; в июле 2033, 2034, 2035, 2036 и 2037 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года; к июлю 2037 года долг должен быть выплачен полностью. Известно, что сумма всех платежей после полного погашения кредита будет равна 2400 тыс. рублей. Сколько рублей составит платёж в 2029 году?

Задача. В июле 2026 года планируется взять кредит на 10 лет в размере 1300 тыс. рублей. Условия его возврата таковы: каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо оплатить одним платежом часть долга; в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года; в июле 2032, 2033, 2034, 2035 и 2036 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года; к июлю 2036 года долг должен быть выплачен полностью. Известно, что сумма всех платежей после полного погашения кредита будет равна 2780 тыс. рублей. Сколько рублей составит платёж в 2027 году?

Задача. В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы: каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года; с февраля по июнь необходимо выплатить одним платежом часть долга; в июле 2026, 2027, 2028, 2029 и 2030 долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года; в июле 2030 года долг должен составлять 800 тысяч рублей; в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же сумму меньше долга на июль предыдущего года. Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.

Задача. В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей. Условия его возврата таковы: в январе каждого года действия кредита долг увеличивается на 10% от суммы долга на конец предыдущего года; в период с февраля по сентябрь необходимо выплатить часть долга; в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же сумму меньше долга на октябрь предыдущего года; в 2033 и 2034 годах выплаты по кредиту равны; к октябрю 2034 года кредит должен быть полностью погашен. Известно, что общая сумма выплат по кредиту должна составить 6025 тыс. рублей. Сколько рублей составит выплата 2031 года?

Задача. В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей. Условия его возврата таковы: в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года; в период с февраля по сентябрь необходимо выплатить часть долга; в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же величину Q рублей меньше долга на октябрь предыдущего года; в 2033 и 2034 годах выплаты по кредиту равны; к октябрю 2034 года кредит должен быть полностью погашен. Найдите величину Q, если общая сумма выплат по кредиту должна составить 4168 тыс. рублей.

Задача. Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 8 млн. рублей.

Задача. Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн. рублей.

Задача. В июле 2023 года планируется взять кредит на 8 лет в размере 800 тыс. рублей. Условия его возврата таковы: каждый январь с 2024 по 2027 год долг возрастает на r % по сравнению с концом предыдущего года; каждый январь с 2028 по 2031 год долг возрастает на 15 % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2031 года кредит должен быть полностью погашен. Найдите r, если общая сумма выплат по кредиту должна составить 1444 тысяч рублей.

Задача. В июле 2025 года планируется взять кредит в банке на сумму 650 тыс. рублей на 10 лет. Условия его возврата таковы: в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года; в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16 % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2035 года кредит должен быть полностью погашен. Найдите общую сумму выплат после полного погашения кредита.

Задача. В июле 2023 года планируется взять кредит на 12 лет в размере 1200 тыс. рублей. Условия его возврата таковы: каждый январь с 2024 по 2029 год долг возрастает на 18 % по сравнению с концом предыдущего года; каждый январь с 2030 по 2035 год долг возрастает на 15 % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга; в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; к июлю 2035 года кредит должен быть полностью погашен. Найдите общую сумму выплат после полного погашения кредита.

Задача. В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. На сколько рублей последняя выплата будет больше первой?

Задача. В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на r % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.

Задача. Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1806000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено ниже. Вариант 1. Каждый январь долг возрастает на 15% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами. Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен. На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?

Задача. Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1962000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено ниже. Вариант 1. Каждый январь долг возрастает на 18% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами. Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен. На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?

Задача. 15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит? (Считайте, что округления при вычислении платежей не производятся.)

Задача. 15 января планируется взять кредит в банке на 49 месяцев. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей? (Считайте, что округления при вычислении платежей не производятся.)

Задача. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: каждый январь долг возрастает на 15% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга, равную 1,587 млн рублей. Сколько миллионов рублей было взято в банке, если известно, что долг был полностью погашен двумя равными платежами (т.е. за два года)?

Задача. В июле года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: каждый январь долг возрастает на 16% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,523 млн рублей. Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (т.е. за два года)?

Задача. В июле года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: каждый январь долг возрастает на 14% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить часть долга, равную 3,249 млн рублей. Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (т.е. за два года)?

Задача. 15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы: 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца; к 15-му числу 11-го месяца кредит должен быть полностью погашен. Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?

Задача. 15 декабря планируется взять кредит в банке на сумму 600 тысяч рублей на n+1 месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 852 тысячи рублей.

Задача. 15 декабря планируется взять кредит в банке на сумму 1000000 рублей на (n+1) месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысячи рублей.

Задача. По вкладу «А» банк в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 12 % в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».

Задача. По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».

Задача. Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?

Задача. Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?

Задача. 15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы: 11-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; 15-го числа 15-го месяца долг составит 100 тысяч рублей; к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.

Задача.15 декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 16 месяцев. Условия его возврата таковы: 1-го числа каждого месяца долг будет возрастать на r % по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; 15-го числа 15-го месяца долг должен быть равен 500 тысяч рублей; к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что сумма всех платежей после полного погашения кредита будет составлять 1228 тысяч рублей.

Задача. 15 мая планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы: 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца с 1-го по 16-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца; к 15-му числу 17-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1472 тысячи рублей?

Задача. Производство х тыс. единиц продукции в q=2x²+5x+10 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q. При каком наименьшем значении p через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении х?

Задача. Производство х тыс. единиц продукции в q=3x²+6x+13 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q. При каком наименьшем значении p через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?

Задача. Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает p человек, то каждый из них получает в сутки 200p рублей. Если на втором объекте работает p человек, то каждый из них получает в сутки (50p+300) рублей. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?

Задача. По бизнес-плану четырёхлетний проект предполагает начальное вложение 25 млн рублей. По итогам каждого года планируется прирост вложенных средств на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.

Задача. По бизнес-плану четырёхлетний проект предполагает начальное вложение 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.

Задача. По бизнес-плану четырёхлетний проект предполагает начальное вложение 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 12 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года вырастут как минимум в полтора раза, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.

Параметры в заданиях ЕГЭ

Задача. Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два решения

Задача. Найдите все значения параметра а, при каждом из которых неравенство

||x + 2a|-3a| + ||3x-a| + 4a| ≤ 7x + 24 выполняется для всех значений х∈[0; 7].

Задача. Найдите все такие значения а, при каждом из которых неравенство

-1 ≤ sinx(a-cos2x) ≤ 1 верно при всех действительных значениях х.

Задача. Найдите все такие значения а, при каждом из которых неравенство

-1 ≤ cosx(cos2x-a-1) ≤ 1 верно при всех действительных значениях х.

Задача. Найдите все значения а, при каждом из которых система уравнений имеет более одного решения.

Задача. Найдите все значения а, при каждом из которых система уравнений имеет более двух решений.

Задача. Найдите все значения параметра а, при каждом из которых множество значений

Задача. Найдите все значения а, при каждом из которых множество значений функции

Задача. Найдите все значения а, при каждом из которых функция

f(x) = x²-4|x-a²|-8x имеет хотя бы одну точку максимума.

Задача. Найдите все значения а, при каждом из которых функция

f(x) = x²-3|x-a²|-5x имеет более двух точек экстремума.

Задача. Найдите все значения параметра а, при каждом из которых уравнение

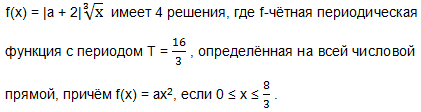
Свойства чисел в заданиях ЕГЭ

Задача. В целочисленной последовательности а₁=3, а₂, … , а_n_-1, a_n=109 сумма любых двух соседних членов последовательности равна или 1, или 3, или 13. а) Приведите пример такой последовательности. б) Может ли такая последовательность состоять из 32 членов? в) Какое наименьшее число членов может быть в такой последовательности?

Задача. Изначально на доске написаны числа 3 и 6. За один ход два числа, написанные на доске, стираются, а вместо них пишутся два других, одно из которых является суммой только что стертых чисел, а второе равно 2х+2, где х – одно из только что стертых чисел. а) Может ли за несколько ходов на доске оказаться число 48? б) Может ли после 80 ходов одно из двух чисел, написанных на доске, оказаться числом 630? в) Сделали 519 ходов. Какое наименьшее значение может принимать разность большего и меньшего из полученных чисел?

Задача. На доске написаны числа 10, 11, 12, 13, … , 50. За один ход разрешается стереть произвольные четыре числа таких, что их сумма больше 134 и не равна ни одной из сумм четвёрок чисел, стёртых на предыдущих ходах. а) Можно ли сделать 5 ходов по описанным правилам? Если да, то приведите пример этих ходов. б) Можно ли сделать 10 ходов по описанным правилам? в) Какое наибольшее число ходов можно сделать?

Задача. На доске было написано 30 натуральных чисел (необязательно различных), каждое их которых не превосходит 40. Среднее арифметическое написанных чисел равнялось 7. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 1, с доски стёрли. а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 14? б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13? в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

Задача. Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу). а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел? б) Могут ли быть одинаковыми все три значения средних арифметических? в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.

Задача. а) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа. б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа? в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа?

Задача. Ученики одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 83 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось. а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился? б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился? в) Известно, что первоначально средний балл участников теста составил 90, средний балл участников, сдавших тест, составил 100, а средний балл участников, не сдавших тест, составил 75. После добавления баллов средний балл участников, сдавших тест, стал равен 103, а не сдавших тест – 79. При каком наименьшем числе участников теста возможна такая ситуация?

Задача. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 3/10 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 5/12 от общего числа учащихся группы, посетивших кино. а) Могло ли быть в группе 8 мальчиков, если дополнительно известно, что всего в группе было 16 учащихся? б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 16 учащихся? в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?

Задача. а) Приведите пример трёхзначного числа, у которого ровно 5 натуральных делителей. б) Существует ли такое трёхзначное число, у которого ровно 15 натуральных делителей? в) Сколько существует таких трёхзначных чисел, у которых ровно 20 натуральных делителей?

Задача. Назовём натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифры, вторая и предпоследняя, и т.д.). Например, числа 121 и 953359 являются палиндромами, а числа 10 и 953359 не являются палиндромами. а) Приведите пример числа-палиндрома, который делится на 15. б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15? в) Найдите 37-е по величине число-палиндром, которое делится на 15.