Решить логарифмическое неравенство
Решите неравенство lg4(x2 – 26)4 – 4lg2(x2 – 26)2 ≤ 240.

Применим формулу для логарифма степени и запишем
lg(x2 – 26)4 как 2lg(x2 – 26)2. А почему не как 4lg(x2 – 26)? Потому что в этом случае число под знаком логарифма должно быть положительным, а не просто не равным нулю, как мы записали в ОДЗ. Это значит, что преобразованное далее неравенство не будет равносильно данному. Итак:
lg4(x2 – 26)4 = (lg(x2 – 26)4 )4 = (2lg(x2 – 26)2 )4 = 24 · (lg(x2 – 26)2 )4 = 16lg4(x2 – 26)2.
Тогда данное неравенство примет вид:
16lg4(x2 – 26)2 – 4lg2(x2 – 26)2 ≤ 240. Делим обе части на 4.
4lg4(x2 – 26)2 – lg2(x2 – 26)2 – 60 ≤ 0.
Сделаем замену. Пусть lg2(x2 – 26)2 = t.
Решим неравенство. 4t2 – t – 60 ≤ 0.
Находим корни квадратного трёхчлена.
4t2 – t – 60 = 0. D = b2 – 4ac = 1 + 960 = 961 = 312.

0 ≤ lg2(x2 – 26)2 ≤ 4.
lg2(x2 – 26)2 ≤ 4. Извлекаем из обеих частей квадратные корни.
| lg(x2 – 26)2| ≤ 2.
-2 ≤ lg(x2 – 26)2 ≤ 2. (см. рис. 2)

Запишем числа -2 и 2 в виде десятичного логарифма.
lg0,01 ≤ lg(x2 – 26)2 ≤ lg100. Логарифмическая функция с основанием 10 является возрастающей, поэтому последнее неравенство равносильно неравенству
0,01 ≤ (x2 – 26)2 ≤ 100. А это неравенство равносильно системе неравенств
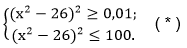
Решаем каждое неравенство системы по отдельности, а затем находим их общее решение. Оно и будет служить решением данного неравенства.

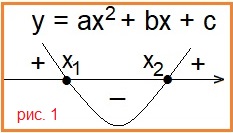
I. (x2 – 26)2 ≥ 0,01; (см. рис.3)
| x2 – 26| ≥ 0,1;
1) x2 – 26 ≤ -0,1
x2 ≤ 25,9.

2) x2 – 26 ≥ 0,1
x2 ≥ 26,1.
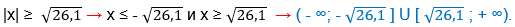
Решаем второе неравенство системы ( * )
II. (x2 – 26)2 ≤ 100;
| x2 – 26| ≤ 10;
-10 ≤ x2 – 26 ≤ 10
16 ≤ x2 ≤ 36;

Полученные решения неравенств I и II покажем синим и зелёным цветом на координатной прямой. Пересечение этих промежутков и будет решением нашего неравенства.


Навигация
Предыдущая статья: ← Тригонометрические уравнения на ЕГЭ
Следующая статья: Фигуры на клетчатой бумаге с размером клетки 1х1 →
В этой же рубрике:
- Тригонометрические уравнения на ЕГЭ
- В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы: каждый январь долг увеличивается на 10%
- 15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы: 1-го числа каждого месяца долг возрастает на 3%
- В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей.
- В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей.



Комментирование закрыто.