В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей
Задача. В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 15% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2033, 2034, 2035, 2036 и 2037 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2037 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2400 тыс. рублей. Сколько рублей составит платёж в 2029 году?
Решение.
Условие «-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
15% банк насчитывает на остаток долга.
0,15 ∙ (1500 + (1500-х) + (1500-2х) + (1500-3х) + (1500-4х)) =
= 0,15 ∙ (5 ∙ 1500 -10х) = 0,15(7500-10х) = (1125-1,5х) тыс. рублей.
Итак, к концу 2032 года (после 5 лет ежегодных выплат) долг составит (1500-5х) тыс. рублей или 5(300-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (300-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,15 ∙ (5(300-х) + 4(300-х) + 3(300-х) + 2(300-х) + (300-х)) =
= 0,15 ∙ 15(300-х) = 2,25 ∙ (300-х) = (675-2,25х) тыс. рублей.
По условию общая сумма выплат 2400 тыс. рублей, значит, сумма выплаченных процентов составит 2400-1500 = 900 тыс. рублей. Составим уравнение.
1125-1,5х + 675-2,25х = 900;
-1,5х-2,25х = 900-1125-675;
-3,75х = -900 | : (-3,75);
х = 240. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 240 тыс. рублей.
Искомый платёж за 2029 год составит эти 240 тыс. рублей плюс 15% от остатка долга, т.е. от суммы 1500-240 = 1260 тыс. рублей, так как в 2028 году уже было погашено 240 тыс. рублей.
Считаем: 240 + 0,15 ∙ 1260 = 240 + 189 = 429 тыс. рублей.
Ответ: 429000 рублей.
Задача. В июле 2026 года планируется взять кредит на 10 лет в размере 1300 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2032, 2033, 2034, 2035 и 2036 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2036 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2780 тыс. рублей. Сколько рублей составит платёж в 2027 году?
Решение.
Условие «-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
20% банк насчитывает на остаток долга.
0,2 ∙ (1300 + (1300-х) + (1300-2х) + (1300-3х) + (1300-4х)) =
= 0,2 ∙ (5 ∙ 1300 -10х) = 0,2(6500-10х) = (1300-2х) тыс. рублей.
Итак, к концу 2031 года (после 5 лет ежегодных выплат) долг составит (1300-5х) тыс. рублей или 5(260-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (260-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,2 ∙ (5(260-х) + 4(260-х) + 3(260-х) + 2(260-х) + (260-х)) =
= 0,2 ∙ 15(260-х) = 3 ∙ (260-х) = (780-3х) тыс. рублей.
По условию общая сумма выплат 2780 тыс. рублей, значит, сумма выплаченных процентов составит 2780-1300 = 1480 тыс. рублей. Составим уравнение.
1300-2х + 780-3х = 1480;
-2х-3х = 1480-1300-780;
-5х = -600 | : (-5);
х = 120. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 120 тыс. рублей.
Искомый платёж за 2027 год составит эти 120 тыс. рублей плюс 20% от взятой суммы кредита в 1300 тыс. рублей, так как в 2027 году состоится самая первая выплата банку.
Считаем: 120 + 0,2 ∙ 1300 = 120 + 260 = 380 тыс. рублей.
Ответ: 380000 рублей.
Найдите все такие значения а, при каждом из которых
ЕГЭ 2022 ФИПИ Вариант 5. Задача 17
Задача. Найдите все такие значения а, при каждом из которых неравенство
-1 ≤ sinx(a-cos2x) ≤ 1 верно при всех действительных значениях х.
Решение. Видео решение этой задачи.
Применим формулу 1-cos2x = 2sin2x.
-1 ≤ sinx(a+2sin2x-1) ≤ 1. Сделаем замену. Пусть sinx = t.
Так как |sinx| ≤ 1 при любом х ∈ (- ∞; +∞),
то t ∈ [-1; 1]. Получаем:
-1 ≤ t(a+2t2 -1) ≤ 1.
Примечательно, что если мы разделим все части последнего двойного неравенства на любое (отрицательное или положительное) значение
t ≠ 0, то получится неравенство:
![]()
Прибавим ко всем частям неравенства выражение -2t2 +1.
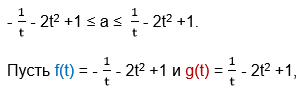
причём, области определения этих функций D(f) = D(g) = [-1; 0) U (0; 1].
Тогда f(t) ≤ а ≤ g(t).
Получается, что число а больше или равно наибольшему значению функции f(t), и в это же время а меньше или равно наименьшему значению функции g(t), т.е.
max f(t) ≤ а ≤ min g(t).
Итак, нам необходимо найти максимум функции f(t) и минимум функции g(t).
Воспользуемся понятием производной.

Найдём промежутки убывания и возрастания функции f(t).
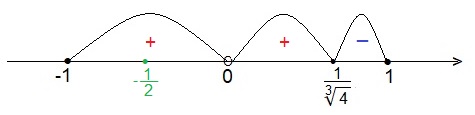

функция f(t) меняет знак с «+» на «-», следовательно, это точка максимума функции. Находим значение максимума функции f(t).
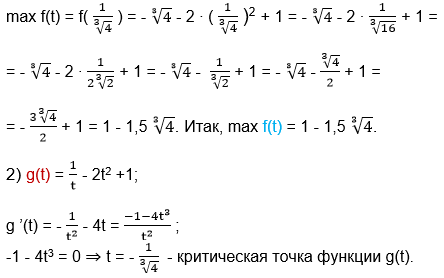
Найдём промежутки убывания и возрастания функции g(t).
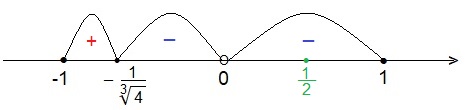

точек минимума не имеет. Это означает, что наименьшее значение функция будет иметь в точке t = 1.
Тогда min g(t) = g(1) = 1 -2 + 1 = 0.
Итак, min g(t) = 0.
Так как max f(t) ≤ а ≤ min g(t),
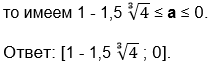
ЕГЭ 2022 ФИПИ Вариант 6. Задача 17
Задача. Найдите все такие значения а, при каждом из которых неравенство
-1 ≤ cosx(cos2x-a-1) ≤ 1 верно при всех действительных значениях х.
Решение.
Применим формулу 1+cos2x = 2cos2x.
-1 ≤ cosx(2cos2x-1-a-1) ≤ 1
-1 ≤ cosx(2cos2x-a-2) ≤ 1. Сделаем замену. Пусть cosx = t.
Так как |cosx| ≤ 1 при любом х ∈ (- ∞; +∞),
то t ∈ [-1; 1]. Получим:
-1 ≤ t(2t2 -a -2) ≤ 1.
Если мы разделим все части последнего двойного неравенства на любое (отрицательное или положительное) значение t ≠ 0, то получится неравенство:

Области определения этих функций D(f) = D(g) = [-1; 0) U (0; 1].
Тогда f(t) ≤ а ≤ g(t).
Получается, что число а больше или равно наибольшему значению функции f(t), и в это же время а меньше или равно наименьшему значению функции g(t), т.е.
max f(t) ≤ а ≤ min g(t).
Итак, нам необходимо найти максимум функции f(t) и минимум функции g(t).
Сделаем это с помощью производной.

Найдём промежутки убывания и возрастания функции f(t).
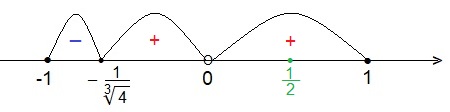
Итак, функция f(t) возрастает при

не имеет точек максимума, поэтому, наибольшее своё значение функция будет иметь в точке t = 1. Находим значение максимума функции f(t).
max f(t) = f(1) = 2-1-2 = -1.
Итак, max f(t) = -1.
Рассмотрим функцию g(t).
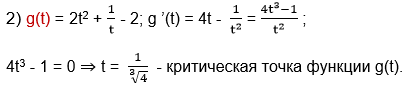
Найдём промежутки убывания и возрастания функции g(t).
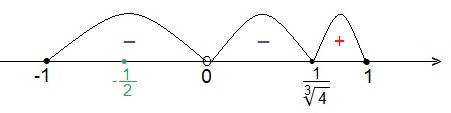

Проценты и кредиты ЕГЭ 2022. Часть 2.
ЕГЭ 2022 ФИПИ. Вариант 11. Задача 15.
В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. На сколько рублей последняя выплата будет больше первой?
Решение.
Первая выплата – это 10% от 1050 тысяч рублей, т.е. 105 тысяч рублей.
Итак, за 2023, 2024 и 2025 годы будут выплачены лишь проценты (по 105 тысяч рублей ежегодно), а сумма долга останется прежней, т.е. равной 1050 тысяч рублей. Обозначим эту сумму через S. Долг следует отдать двумя равными платежами. Обозначим один такой платёж через Х.
2026 год.
Январь. Сумма долга увеличится на 10% и составит 1,1S тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга. Тогда ему останется выплатить (1,1S-Х) тысяч рублей.
2027 год.
Январь. Банк начислит 10% на остаток долга.
Теперь долг равен 1,1(1,1S-Х) тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга, и долг будет погашен. Получаем равенство:
1,1(1,1S-Х)-Х=0;
1,21S-1,1Х-Х=0;
1,21S=2,1Х;
Х=1,21S : 2,1.
Подставляем значение S=1050 и получим:
Х=1,21 ∙ 1050 : 2,1;
Х=605 тысяч рублей. Это последняя выплата.
605-105=500 тысяч рублей. На столько последняя выплата будет больше первой.
Ответ: 500 000 рублей.
Экономические задачи ЕГЭ Это страница с нужной вам задачей
ЕГЭ 2022 ФИПИ. Вариант 12. Задача 15.
В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на r % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.
Решение.
Итак, за 2023, 2024 и 2025 годы будут выплачены лишь проценты, а сумма долга останется прежней, т.е. равной 220 тысяч рублей. Обозначим эту сумму через S. Далее долг следует отдать двумя равными платежами. Обозначим один такой платёж через Х.
2026 год.
Январь. Сумма долга увеличится на r % и составит (1+0,01r)S тысяч рублей. Сделаем замену переменной. Пусть 1+0,01r=k. Итак, после начисления процентов сумма долга равна kS.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга. Тогда ему останется выплатить (kS-Х) тысяч рублей.
2027 год.
Январь. Банк начислит r % на остаток долга.
Долг станет равным k(kS-Х) тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга, и долг будет погашен. Получаем равенство:

Это выплачено за 2026 и 2027 годы. А за первые три года кредитования выплачивались лишь проценты: r % от взятой суммы кредита.
Эта сумма равна 0,01r ∙ 220=2,2r.
За три года (2023, 2024 и 2025 годы) будет выплачено 6,6r тысяч рублей.
Выразим r через k.
Так как 1+0,01r=k, то r=100k-100.
Тогда 6,6r=660k-660.
Следовательно, за пять лет должно быть выплачено 2X+6,6r или

Умножим обе части равенства на (1+k).
440k2+660k-660+660k2-660k=420+420k;
1100k2-420k-1080=0. Делим равенство на 20.
55k2-21k-54=0.
Решаем квадратное уравнение относительно переменной k>0.

Возвращаемся к переменной r.
r=100k-100;
r=100 ∙1,2-100;
r=20.
Ответ: 20%.
ЕГЭ 2022 ФИПИ. Вариант 13. Задача 15.
Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1806000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено ниже.
Вариант 1. Каждый январь долг возрастает на 15% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами.
Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен.
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?
Решение.
1) Рассуждаем согласно варианту 1.
Обозначим сумму кредита через S. Пусть S=1806 тыс. рублей.
1 год. Январь. Банк начислит 15%, и долг станет равным 1,15S.
Февраль-июнь. Клиент делает первый платёж, равный Х тыс. рублей. Весь этот платёж засчитывается и долг становится равным (1,15S-Х) тыс. рублей.
2 год. Январь. Банк начислит 15%, и долг станет равным 1,15(1,15S-Х) тыс. рублей.
Февраль-июнь. Клиент делает второй платёж, равный первому, т.е. Х тыс. рублей. И этот платёж полностью засчитывается. Долг погашен. Имеет место равенство: 1,15(1,15S-Х)-Х=0. Решаем уравнение и находим значение Х.
1,152 ∙ S-1,15X-X = 0;
1,152 ∙ S = 2,15X;
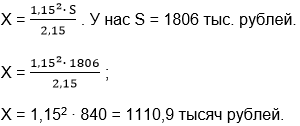
Таким образом, за два года клиент выплатит банку 2Х=2221,8 тысяч рублей или 2221800 рублей.
2) Рассмотрим условия кредитования по варианту 2.
В условии сказано: «со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца», поэтому обозначим эту величину через х тысяч рублей. Тогда вся сумма, взятая в кредит, равна 24х. Мы ее знаем, это 1806 тысяч рублей, но рассуждать удобнее с использованием введённой переменной х. Почему? Потому что проценты банк ежемесячно начисляет на остаток долга, т.е. сначала на 24х, через месяц на 23х и т.д. Подсчитаем начисленные банком проценты за всё время кредитования.
Это 2% от 24х, от 23х и т.д. Получаем:
0,02(24х+23х+22х+…+2х+х).
Сумму в скобках найдём по формуле суммы первых n членов арифметической прогрессии:
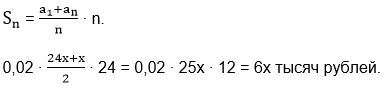
Банку нужно будет выплатить взятую сумму 24х плюс проценты 6х. Итого 30х.
Так как 24х=1806 тысяч рублей, то х=1806:24=75,25 тысяч рублей.
Итак, по варианту 2 нужно будет выплатить
30 ∙ 75,25 = 2257,5 тысяч рублей или 2257500 рублей.
Вариант 1 более выгодный, так как платить меньше, разница в выплаченных суммах составит:
2257500-2221800=35700 рублей.
Ответ: 35700 рублей.
ЕГЭ 2022 ФИПИ. Вариант 14. Задача 15.
Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1962000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено ниже.
Вариант 1. Каждый январь долг возрастает на 18% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами.
Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен.
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?
Задача аналогичная предыдущей. Поменялись сумма кредита и процент по 1 варианту кредитования! Ах, да! Ещё имя клиента!
Решение.
1) Рассуждаем согласно варианту 1.
Обозначим сумму кредита через S. Пусть S=1962 тыс. рублей.
1 год. Январь. Банк начислит 18%, и долг станет равным 1,18S.
Февраль-июнь. Клиент делает первый платёж, равный Х тыс. рублей. Весь этот платёж засчитывается и долг становится равным (1,18S-Х) тыс. рублей.
2 год. Январь. Банк начислит 18%, и долг станет равным 1,18(1,18S-Х) тыс. рублей.
Февраль-июнь. Клиент делает второй платёж, равный первому, т.е. Х тыс. рублей. И этот платёж полностью засчитывается. Долг погашен. Имеет место равенство: 1,18(1,18S-Х)-Х=0. Решаем уравнение и находим значение Х.
1,182 ∙ S-1,18X-X = 0;
1,182 ∙ S = 2,18X;

Таким образом, за два года клиент выплатит банку 2Х=2506,32 тысяч рублей или 2506320 рублей.
2) Рассмотрим условия кредитования по варианту 2.
В условии сказано: «со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца», поэтому обозначим эту величину через х тысяч рублей. Тогда вся сумма, взятая в кредит, равна 24х. Мы ее знаем, это 1962000 рублей. Подсчитаем начисленные банком проценты за всё время кредитования.
Это 2% от 24х, от 23х, от 22х, от 21х и т.д. до последнего месяца, когда остаток будет х тыс. рублей. Получаем:
0,02(24х+23х+22х+…+2х+х). Сумму в скобках найдём по формуле суммы первых n членов арифметической прогрессии:

Это проценты за всё время кредитования.
Банку нужно будет выплатить взятую сумму 24х плюс проценты 6х. Итого 30х.
Так как 24х=1962000 рублей, то х=1962000:24=81750 рублей.
Итак, по варианту 2 нужно будет выплатить
30 ∙ 81750 = 2452500 рублей.
Видим, что вариант 2 более выгодный, так как платить меньше, разница в выплаченных суммах составит:
2506320-2452500=53820 рублей.
Ответ: 53820 рублей.
ЕГЭ 2022 ФИПИ. Вариант 15. Задача 15.
15 января планируется взять кредит в банке на 2 года. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за 15-й месяц кредитования нужно выплатить 44 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
Решение. Обозначим через х тыс. рублей одну и ту же сумму, на которую долг будет уменьшаться ежемесячно. По сути х – это ежемесячный платёж без процентов, а в кредит на два года, т.е. на 24 месяца было взято 24х тысяч рублей. Банку нужно будет вернуть эти 24х тысяч рублей плюс проценты, которые банк будет начислять 1-го числа каждого месяца. Проценты начисляются на остаток долга.
Проценты за всё время кредитования составляют:
![]()
Итого отдать придётся 24х+3х=27х тысяч рублей.
На 15-й месяц кредитования остаток долга будет равен 10х тысяч рублей, так как на х тысяч рублей долг уменьшался ежемесячно. Проценты на этот остаток составят 0,01 ∙ 10х = 0,1. Следовательно, за 15-й месяц банком определена сумма для выплаты х+0,1х=1,1х. По условию задачи эта сумма равна 44 тыс. рублей. Решаем уравнение:
1,1х = 44 → х = 40 тыс. рублей.
Итак, за всё время кредитования банку нужно будет отдать
27 ∙ 40 = 1080 тыс. рублей = 1080000 рублей.
Ответ: 1080000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 16. Задача 15.
15 января планируется взять кредит в банке на 3 года. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
Решение. Обозначим через х тыс. рублей ежемесячный платёж без процентов, а в кредит на три года, т.е. на 36 месяцев было взято 36х тысяч рублей. Банку нужно будет вернуть эти 36х тысяч рублей плюс проценты, которые банк будет начислять 1-го числа каждого месяца. Проценты начисляются на остаток долга.
Проценты за всё время кредитования составят:
![]()
Итого отдать банку придётся 36х+6,66х=42,66х тысяч рублей.
По условию за 24-й месяц нужно выплатить 45,2 тысяч рублей. Эта сумма складывается из ежемесячного платежа без процентов, который мы обозначили через х, и процентов на остаток вклада по прошествии 23 месяцев кредитования. Остаток будет равен 13х.
х + 0,01 ∙ 13х = 1,13х. Получаем уравнение:
1,13х = 45,2 → х = 40 тыс. рублей.
Итак, за всё время кредитования банку нужно будет отдать
42,66 ∙ 40 = 1706,4 тыс. рублей = 1706400 рублей.
Ответ: 1706400 рублей.
ЕГЭ 2022 ФИПИ. Вариант 35. Задача 15.
15 января планируется взять кредит в банке на 24 месяца. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?
Решение. Пусть ежемесячный платеж (без процентов) составляет х рублей. Тогда кредит был выдан в размере 24х рублей. За второй год кредитования (за последние 12 месяцев) нужно вернуть 12х рублей (долг без процентов) плюс проценты, т.е. сумму процентов за каждый из последних 12-то месяцев. По условию эта сумма равна 339000 рублей. Получаем уравнение:
12х + (12х + 11х + 10х + … + х) ∙ 0,02 = 339000;
12х + (12х+х)/2 ∙ 12 ∙ 0,02 = 339000;
12х + 13х ∙ 6 ∙ 0,02 = 339000;
12х + 1,56х = 339000;
13,56х = 339000; х = 339000 : 13,56; х = 25000.
Итак, ежемесячный платеж (без процентов) составляет 25000 рублей.
За первый год кредитования (за первые 12 месяцев) необходимо выплатить:
12х + (24х + 23х + 22х + … + 13х) ∙ 0,02 = 12х + (24х+13х)/2 ∙ 12 ∙ 0,02 =
= 12х + 37х ∙ 6 ∙ 0,02 = 12х + 4,44х = 16,44х = 16,44 ∙ 25000 = 411000 рублей.
Ответ: 411000.
Проценты и кредиты ЕГЭ 2022
ЕГЭ 2022 ФИПИ. Вариант 1. Задача 15.
В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года;
— в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?
Экономические задачи ЕГЭ Это страница с нужной вам задачей
Решение.
Так как «- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года», то обозначим эту величину через х тысяч рублей.
Тогда общая сумма кредита 8х, а остатки долга, на которые и начисляются ежегодно проценты в январе, по годам составят:
2026 год – 8х;
2027 год – 7х;
2028 год – 6х;
2029 год – 5х;
2030 год – 4х;
2031 год – 3х;
2032 год – 2х;
2033 год – х.
За первые 4 года банк начислит по 20% ежегодно, и проценты составят:
0,2(8х+7х+6х+5х)=0,2 ∙ 26х=5,2х тысяч рублей.
За вторые 4 года банк начислит по 18% ежегодно, и проценты составят:
0,18(4х+3х+2х+х)=1,8х тысяч рублей.
Общая сумма процентов за 8 лет составит 5,2х+1,8х=7х тысяч рублей.
Итак, банку придётся отдать 8х тысяч рублей, взятых в кредит, плюс 7х тысяч рублей процентов за всё время кредитования.
Итого общая сумма выплат 15х. По условию это 1125 тысяч рублей.
15х=1125;
х=1125 : 15;
х=75 тысяч рублей.
Таким образом, в кредит планируется взять 8 ∙ 75 = 600 тысяч рублей.
Ответ: 600 000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 2. Задача 15.
В июле 2023 года планируется взять кредит в банке на 10 лет. Условия его возврата таковы:
— каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
— каждый январь с 2029 по 2033 год долг возрастает на 16 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Найдите сумму, которую планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей.
Решение.
Обозначим через х тысяч рублей эту «одну и ту же сумму», на которую долг уменьшается ежегодно все 10 лет.
Следовательно, планируется взять в долг 10х тысяч рублей, а отдать придётся эти 10х тысяч рублей плюс проценты за все 10 лет, которые банк будет начислять ежегодно в январе на остатки долга, т.е. сначала на 10х, потом на 9х, затем на 8х и т.д.
С 2024 по 2028 год долг возрастает на 18%.
Тогда за первые 5 лет банк начислит:
0,18(10х+9х+8х+7х+6х)=7,2х тысяч рублей.
С 2029 по 2033 год долг возрастает на 16%.
А за вторые 5 лет банк начислит:
0,16(5х+4х+3х+2х+х)=2,4х тысяч рублей.
Итак, банку за всё время нужно будет выплатить
10х+7,2х+2,4х или 1470 тысяч рублей. Решаем уравнение:
10х+7,2х+2,4х=1470;
19,6х=1470;
х=1470 : 19,6;
х=75 тысяч рублей.
Таким образом, в кредит планируется взять 10 ∙ 75 = 750 тысяч рублей.
Ответ: 750 000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 5. Задача 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на 20% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Решение.
Читаем условие: «- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года». И мы знаем эту величину:
300 : 6 = 50 тысяч рублей, но для удобства обозначим эту сумму 50 тысяч рублей через х.
Банк будет начислять проценты на остатки долга, т.е. на 6х, 5х, 4х, 3х, 2х и х тысяч рублей.
За первые 3 года долг возрастает на 20% ежегодно, и проценты составят:
0,2(6х+5х+4х)=3х тысяч рублей.
За вторые 3 года банк начислит по r % ежегодно, и проценты составят:
0,01r ∙ (3х+2х+х)=0,06rх тысяч рублей.
Общая сумма выплат составит 6х+3х+0,06rх тысяч рублей.
По условию это 498 тысяч рублей. Получаем равенство:
6х+3х+0,06rх=498;
9х+0,06rх=498. Но у нас х=50 тысяч рублей.
9 ∙ 50+0,06r ∙ 50=498;
450+3r=498;
3r=48;
r =16%.
Ответ: 16.
ЕГЭ 2022 ФИПИ. Вариант 31. Задача 15.
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 8 млн. рублей.
Решение.
Пусть кредит составит S млн рублей, где S – целое число. За 1-й и 2-й годы заёмщик выплатит по условию по 20 % от суммы кредита,
т.е. 0,2S+0,2S=0,4S.
Долг остался прежним S млн рублей
Будем считать, что берётся кредит S на 2 года (3-й и 4-й). Так как отдавать нужно равными платежами, то обозначим этот ежегодный платёж (без процентов) через Х. Тогда S=2X.
За 2 года (3-й и 4-й) будут выплачены эти 2Х млн рублей плюс проценты с этой суммы, всего
2Х+0,2 ∙ (2Х+Х) = 2Х+0,6Х = 2,6Х млн рублей.
Выразим 2,6Х через S.
Так как S = 2X, то X = S/2, поэтому 2,6X = 1,3S.
Итого за четыре года будет выплачено:
0,4S+1,3S = 1,7S млн рублей.
По условию эта сумма должна быть больше 8 млн рублей.
1,7S > 8, отсюда S = 5 – наименьшее целое число.
Ответ: 5 млн рублей.
ЕГЭ 2022 ФИПИ. Вариант 32. Задача 15.
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн. рублей.
Решение.
Пусть кредит составит S млн рублей, где S – целое число. За 1-й и 2-й годы заёмщик выплатит по условию по 25 % от суммы кредита,
т.е. 0,25S+0,25S=0,5S.
Долг остался прежним S млн рублей
Будем считать, что берётся кредит S на 2 года (3-й и 4-й). Так как отдавать нужно равными платежами, то обозначим этот ежегодный платёж (без процентов) через Х. Тогда S=2X.
За 2 года (3-й и 4-й) будут выплачены эти 2Х млн рублей плюс проценты с этой суммы, всего
2Х+0,25 ∙ (2Х+Х) = 2Х+0,75Х = 2,75Х млн рублей.
Выразим 2,75Х через S.
Так как S = 2X, то X = S/2, поэтому 2,75X = 1,375S.
Итого за четыре года будет выплачено:
0,5S+1,375S = 1,875S млн рублей.
По условию эта сумма должна быть больше 9 млн рублей.
1,875S > 9;
S > 4,8;
отсюда S = 5 – наименьшее целое число.
Ответ: 5 млн рублей.
ЕГЭ 2022 ФИПИ. Вариант 6. Задача 15.
В июле 2023 года планируется взять кредит на 8 лет в размере 800 тыс. рублей. Условия его возврата таковы:
— каждый январь с 2024 по 2027 год долг возрастает на r % по сравнению с концом предыдущего года;
— каждый январь с 2028 по 2031 год долг возрастает на 15 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Найдите r, если общая сумма выплат по кредиту должна составить 1444 тысяч рублей.
Решение.
Читаем условие: «- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года». И мы знаем эту величину:
800 : 8 = 100 тысяч рублей, но для удобства обозначим эту сумму 100 тысяч рублей через х.
Банк будет начислять проценты на остатки долга, т.е. на 8х, 7х, 6х, 5х, 4х, 3х, 2х и х тысяч рублей.
За первые 4 года банк начислит по r % ежегодно, и проценты составят:
0,01r ∙ (8х+7х+6х+5х)=0,26rх тысяч рублей.
За последующие 4 года долг возрастает на 15% ежегодно, и проценты составят:
0,15(4х+3х+2х+х)=1,5х тысяч рублей.
Общая сумма выплат составит 8х+0,26rх+1,5х тысяч рублей.
По условию это 1444 тысяч рублей. Получаем равенство:
8х+0,26rх+1,5х=1444;
9,5х+0,26rх=1444. Значение х=100 тысяч рублей.
9,5 ∙ 100+0,26r ∙ 100=1444;
950+26r=1444;
26r=494;
r =19%.
Ответ: 19.
ЕГЭ 2022 ФИПИ. Вариант 9. Задача 15.
В июле 2025 года планируется взять кредит в банке на сумму 650 тыс. рублей на 10 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
— в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Решение.
Так как «- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года», то обозначим эту величину через х тысяч рублей.
На самом деле, мы эту сумму знаем: это 650 : 10=65 тысяч рублей. А для чего берём эту сумму за х? Исключительно для удобства рассуждений!
Итак, 65 тыс. руб.=х.
Тогда общая сумма кредита 10х, а остатки долга, на которые и начисляются ежегодно проценты в январе, по годам составят:
2026 год – 10х;
2027 год – 9х;
2028 год – 8х;
……………….
2035 год – х.
За первые 5 лет банк начислит по 19% ежегодно, и проценты составят:
0,19(10х+9х+8х+7х+6х)=0,19 ∙ 40х=7,6х тысяч рублей.
За последующие 5 лет банк начислит по 16% ежегодно, и проценты составят:
0,16(5х+4х+3х+2х+х)=2,4х тысяч рублей.
Общая сумма процентов за 10 лет составит 7,6х+2,4х=10х тысяч рублей.
Итак, банку придётся отдать 10х тысяч рублей, взятых в кредит, плюс 10х тысяч рублей процентов за всё время кредитования.
Итого общая сумма выплат 20х. А мы знаем, что х=65 тысяч рублей, поэтому общая сумма выплат после полного погашения кредита составит
20 ∙ 65 = 1300 тысяч рублей.
Ответ: 1300 000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 10. Задача 15.
В июле 2023 года планируется взять кредит на 12 лет в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь с 2024 по 2029 год долг возрастает на 18 % по сравнению с концом предыдущего года;
— каждый январь с 2030 по 2035 год долг возрастает на 15 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Решение.
Читаем условие: «- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года». И мы знаем эту величину:
1200 : 12 = 100 тысяч рублей, но для удобства обозначим эту сумму 100 тысяч рублей через х.
Банк будет начислять проценты на остатки долга, т.е. на 12х, 11х, 10х, 9х, 8х, 7х, 6х, 5х, 4х, 3х, 2х и х тысяч рублей.
За первые 6 лет банк начислит по 18% ежегодно, и проценты составят:
0,18(12х+11х+10х+9х+8х+7х)=0,18 ∙ 57х=10,26х тысяч рублей.
За последующие 6 лет банк начислит по 15% ежегодно, и проценты составят:
0,15(6х+5х+4х+3х+2х+х)=0,15 ∙ 21х=3,15х тысяч рублей.
Общая сумма процентов за 12 лет составит 10,26х+3,15х=13,41х тысяч рублей.
Итак, банку придётся отдать 12х тысяч рублей, взятых в кредит, плюс 13,41х тысяч рублей процентов за всё время кредитования.
Итого общая сумма выплат 25,41х тысяч рублей. А мы знаем, что х=100 тысяч рублей, поэтому общая сумма выплат после полного погашения кредита составит
25,41 ∙ 100 = 2541 тысяч рублей.
Ответ: 2 541 000 рублей.
Назовём натуральное число палиндромом
Задача. Назовём натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифры, вторая и предпоследняя, и т.д.). Например, числа 121 и 953359 являются палиндромами, а числа 10 и 953359 не являются палиндромами.
а) Приведите пример числа-палиндрома, который делится на 15.
б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?
в) Найдите 37-е по величине число-палиндром, которое делится на 15.
Решение.
Так как наше число-палиндром должно делиться на 15, то оно должно делиться и на 5 и на 3. На 5 делятся числа, оканчивающиеся на 0 и на 5. Однако, число не может начинаться с нуля, а, значит, и не может оканчиваться нулём, поэтому искомые числа будут оканчиваться на 5 и начинаться тоже с цифры 5. Имеем в виду, что на 3 делится число, сумма цифр которого делится на 3.
а) Так как 55 не делится на 3, то среди двузначных чисел нет чисел-палиндромов, делящихся на 15. Из трёхзначных чисел наименьшим числом-палиндромом, делящимся на 15, будет число 525. Оно оканчивается на «5», поэтому делится на 5, а также число 525 делится на 3, так как сумма цифр этого числа 5+2+5=12 делится на 3.
Так как в пункте в) нам нужно будет указать 37-е по величине число-палиндром, которое делится на 15, то найдём все трёхзначные и четырёхзначные числа-палиндромы, которые делится на 15. Все наши числа начинаются и оканчиваются на «5», поэтому нам остаётся только позаботиться о том, чтобы сумма цифр каждого из чисел делилась на 3. Так как в любом искомом числе-палиндроме уже есть две пятерки (5+5=10), то общая сумма цифр трёхзначного числа-палиндрома может быть равна 12 или 15 или 18, т.е. в серединке между двумя «пятёрками» может стоять цифра 2 (число 525) или 5 (число 555) или 8 (число 585). Таким образом, среди трёхзначных чисел всего три числа-палиндрома, которые делятся на 15.
Переходим к четырёхзначным числам. Первая и последняя цифры – пятёрки, а сумма двух (одинаковых) цифр, стоящих в середине может быть равна 2 (число 5115) или 8 (число 5445) или 14 (число 5775). Других вариантов нет. Таким образом, среди четырёхзначных чисел тоже нашлись всего три числа-палиндрома, которые делятся на 15.
б) Приступаем к нахождению пятизначных чисел-палиндромов, делящихся на 15. Нас будет интересовать сумма трёх средних цифр каждого пятизначного числа. Так как общая сумма всех цифр пятизначного числа должна делиться на 3, то она может быть равна или 12 или 15 или 18 или 21 или 24 или 27 или 30 или 33 или 36. Учитывая сумму первой и последней цифр (5+5=10), заключаем, что сумма средних трёх цифр может быть равна 2 или 5 или 8 или 11 или 14 или 17 или 20 или 23 или 26. Выпишем в порядке возрастания эти трёхзначные числа-палиндромы, стоящие между двумя «пятёрками» в искомых пятизначных числах-палиндромах, делящихся на 15.
020, 050, 080, 101, 131, 161, 191, 212, 242, 272, 323, 353, 383, 404, 434, 464, 494, 515, 545, 575, 626, 656, 686, 707, 737, 767, 797, 818, 848, 878, 929, 959, 989. Пересчитываем. Их 33, и это числа:
50205, 50505, 50805, 5105, 51315, 51615, 51915, 52125, 52425, 52725, 53235, 53535, 53835, 54045, 54345, 54645, 54945, 55155, 55455, 55755, 56265, 56565, 56865, 57075, 57375, 57675, 57975, 58185, 58485, 58785, 59295, 59595, 59895.
в) Так как число 50205 уже 7-ое по счёту число-палиндром, делящееся на 15 (помните, были три трёхзначных числа и три четырёхзначных числа?), то на 37-ом месте стоит число 59295.
Ответ: а) 525; б) 33; в) 59295.
Приведите пример трёхзначного числа, у которого ровно 5
Задача. а) Приведите пример трёхзначного числа, у которого ровно 5 натуральных делителей.
б) Существует ли такое трёхзначное число, у которого ровно 15 натуральных делителей?
в) Сколько существует таких трёхзначных чисел, у которых ровно 20 натуральных делителей?
Решение.
Мы умеем записывать каноническое разложение числа на простые множители. Например, 24 = 23 ∙ 3 – каноническое разложение числа 24 на простые множители. Существует правило:
если число можно представить в виде
![]()
где m1, m2, … , mk – натуральные показатели, то количество делителей числа n будет равно (m1+1) ∙ (m2+1) ∙ ∙∙∙ ∙ (mk+1).
Так, например, у числа 24 = 23 ∙ 31 всего (3+1)(1+1) = 4 ∙ 2 = 8 делителей.
Проверьте: 24 делится на 1; 2; 3; 4; 6; 8; 12 и на 24.
а) Трёхзначное число, у которого 5 делителей, в каноническом виде есть произведение степеней с такими натуральными делителями m1, m2, … , mk,
чтобы (m1+1) ∙ (m2+1) ∙ ∙∙∙ ∙ (mk+1) = 5. Так как 5 = 1 ∙ 5, то показатели степеней должны быть 0 и 4.
![]()
Подойдёт а=5. Получаем 1 ∙ 54 = 625. Это число имеет 5 делителей: 1; 5; 25; 125; 625.
б) 15 = 3 ∙ 5. Следовательно, будем искать число, каноническое разложение которого равно
![]()
Возьмём а1 = 3; а2 = 2 для примера.
Получим 32 ∙ 24 = 9 ∙ 16 = 144 – трёхзначное число.
У числа 144 ровно 15 делителей: 1; 2; 3; 4; 6; 8; 9; 12; 16; 18; 24; 36; 48; 72; 144.
Если возьмём а1 = 2; а2 = 3, то получим 22 ∙ 34 = 4 ∙ 81 = 324 – тоже трёхзначное число, и у него тоже ровно 15 делителей:
1; 2; 3; 4; 6; 9; 12; 18; 27; 36; 54; 81; 108; 162; 324.
в) 20 = 4 ∙ 5, значит, возможно произведение двух степеней с натуральными основаниями, показатели которых 3 и 4.
![]()
Например, 23 ∙ 34 = 648 (подходит, это 1-ое трёхзначное число),
24 ∙ 33 = 432 (2-ое число), 24 ∙ 53 = 2000 (это четырёхзначное число, не подойдёт).
20 = 2 ∙ 2 ∙ 5. Это означает, что каноническое разложение может представлять собой произведение трёх степеней с простыми натуральными основаниями и показателями 1, 1 и 4.
![]()
Подберём простые натуральные числа в качестве оснований степеней а1, а2 и а3 так, чтобы в результате получались трёхзначные числа.
24 ∙ 3 ∙ 5 = 240 (3-е число),
24 ∙ 3 ∙ 7 = 336 (4-ое число),
24 ∙ 3 ∙ 11 = 528 (5-ое число),
24 ∙ 3 ∙ 13 = 624 (6-ое число),
24 ∙ 3 ∙ 17 = 816 (7-ое число),
24 ∙ 3 ∙ 19 = 912 (8-ое число),
24 ∙ 5 ∙ 7 = 560 (9-ое число),
24 ∙ 5 ∙ 11 = 880 (10-ое число),
34 ∙ 2 ∙ 5 = 810 (11-ое число),
34 ∙ 2 ∙ 7 = 1134 (не подойдёт).
Ответ: а) 625; б) да, 144; в) 11.
Каждый из группы учащихся сходил в кино или в театр
Задача. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 3/10 от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 5/12 от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 8 мальчиков, если дополнительно известно, что всего в группе было 16 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 16 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?
Решение.
а) Дробь 3/10 – несократимая. Заметим, что не могла быть первоначальной дробь 6/20 , т.к. в группе всего 16 учащихся.
Вывод: в театр сходили 3 мальчика и 10-3=7 девочек.
м м м д д д д д д д
Аналогично, рассматривая дробь 5/12 , заключаем, что в кино сходили 5 мальчиков и 12-5=7 девочек.
м м м м м д д д д д д д
Если предположить, что в группе 8 мальчиков, то, поскольку всего 16 человек, девочек тоже 8. А это означает, что в театр ходили 6+1 девочка, в кино ходили те же 6 плюс одна другая девочка. Все сходится: в группе 16 человек: 8 мальчиков и 8 девочек. Ответ: да.
б) 8 мальчиков. Это вытекает из рассуждений в пункте а) и из условия: каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр.
в) Также из пункта а) следует, что наименьшее число девочек в группе равно 7, т.е. все эти семь девочек ходили и в кино и в театр. А так как мальчиков 8, то общее количество детей равно 7+8=15. Следовательно, доля девочек от общего количества учащихся составляет 7/15 .
Ответ: а) да; б) 8; в) 7/15.
Ученики одной школы писали тест
Задача. Ученики одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 83 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 90, средний балл участников, сдавших тест, составил 100, а средний балл участников, не сдавших тест, составил 75. После добавления баллов средний балл участников, сдавших тест, стал равен 103, а не сдавших тест – 79. При каком наименьшем числе участников теста возможна такая ситуация?
Решение.
а) Да, могло. Пример: пусть получены результаты теста 90, 90, 90, 78, 78, 78, 60, 60, 60.
Средний балл шести участников, не сдавших тест, равен
(78+78+78+60+60+60) : 6 = 69. После добавления всем участникам по 5 баллов результаты будут такими: 95, 95, 95, 83, 83, 83, 65, 65, 65.
Средний балл трёх участников, не сдавших тест равен (65+65+65) : 3 = 65. Как видим, средний балл участников, не сдавших тест, понизился.
б) Да, так могло быть. Вернемся к примеру, рассмотренному в пункте а). Итак, пусть получены результаты теста 90, 90, 90, 78, 78, 78, 60, 60, 60. Сдали тест всего трое учащихся.
Средний балл участников, сдавших тест равен (90+90+90) : 3 = 90.
После добавления всем участникам по 5 баллов результаты будут такими: 95, 95, 95, 83, 83, 83, 65, 65, 65. Участников, сдавших тест уже шестеро. Средний балл равен (95+95+95+83+83+83) : 6 = 89. Таким образом, средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился.
в) Пусть первоначально было х участников, сдавших тест и у участников, не сдавших тест.
Зная, что первоначально средний балл участников теста составил 90, средний балл участников, сдавших тест, составил 100, а средний балл участников, не сдавших тест, составил 75, можно записать равенство:
90(х+у) = 100х+75у. Упростим это выражение:
90х+90у=100х+75у, отсюда 10х=15у или 2х=3у.
Затем всем участникам добавили по 5 баллов, и, возможно, это помогло р учащимся пополнить списки сдавших тест.
Тогда сдали тест (х+р) участников, а не сдавших будет (у-р) человек.
Зная, что при этом средний балл участников, сдавших тест, стал равен 103, а не сдавших тест – 79, составим равенство:
95(х+у) = 103(х+р)+79(у-р). Упрощаем это выражение.
95х+95у = 103х+103р+79у-79р;
8х+24р=16у или 2х+6р=4у. Так как 2х=3у, то 3у+6р=4у, тогда у=6р.
Так как мы выясняем, при каком наименьшем числе участников теста возможна такая ситуация, то возьмём р=1. Это будет означать, что добавление пяти баллов каждому участнику помогло лишь одному из них попасть в списки сдавших тест.
Тогда у=6 – это количество участников, не сдавших тест при первоначальном подсчёте баллов;
х = (3 ∙ 6) : 2 = 9 – это количество участников, сдавших тест при первоначальном подсчёте баллов. Вывод: х+у = 9+6 = 15 – наименьшее число участников, при которых стала возможной описанная в пункте в) ситуация.
Ответ: а) да; б) да; в) 15.
Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа
Задача. а) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа?
Решение.
а) 2355.
На самом деле, сумма 2+3+5+5=15, произведение 2 ∙ 3 ∙ 5 ∙ 5 = 150 и 150 > 15 в 10 раз.
б) Пусть искомое четырёхзначное число записано цифрами x, y, z и t (в любой последовательности). По условию можно составить равенство:

то какие-то три из чисел x, y, z и t должны быть кратны числам 5 и 7. Но каждое из чисел x, y, z и t не меньше 1 и не больше 9, поэтому три числа из четырёх равны 5, 5 и 7. Пусть x=5, y=5, z=7.
![]()
отсюда после сокращения дроби получим 17 + t = t. Это уравнение решений не имеет, следовательно, нет такого четырёхзначного числа, произведение цифр которого в 175 раз больше суммы цифр этого числа.
в) Будем искать такие цифры x, y, z и t, чтобы выполнялось равенство:
![]()
Так как 50 = 2 ∙ 5 ∙ 5, то две из четырёх цифр равны по 5, а третья кратна числу 2, т.е. может быть равна 2 или 4 или 6 или 8. Пусть x=5, y=5, z=2. Тогда получим уравнение
![]()
Отсюда 12 + t = t. Это уравнение решений не имеет, поэтому возьмём z=4.
![]()
отсюда 14 + t = 2t или t=14. Однако, t – натуральное число, меньшее или равное 9, следовательно, z=4 не подойдёт.
Пусть z=6, тогда получаем равенство:
![]()
и после сокращения дроби имеем: 16 + t = 3t, откуда t = 8.
Проверка.
Сумма 5 + 5 + 6 + 8 = 24; произведение 5 ∙ 5 ∙ 6 ∙ 8 = 1200 и 1200 > 24 в 50 раз.
Искомые четырёхзначные числа мы получим перестановкой цифр 5, 5, 6 и 8.
Так как это перестановка с повторениями, то количество всех четырёхзначных чисел равно 4! : 2! = 1 ∙ 2 ∙ 3 ∙ 4 : (1 ∙ 2) = 24 : 2 = 12. Вот эти числа:
5568, 5586, 5685, 5865, 6855, 8655, 5658, 5856, 6585, 8565, 6558, 8556.
Ответ: а) 2355; б) нет; в) 5568.
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число
Задача. Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
Решение.
а) Да. Возьмём группы:
1) 1, 2, 8 и 9. Среднее арифметическое (1+2+8+9) : 4 = 5.
2) 3 и 7. Среднее арифметическое (3+7) : 2 = 5.
3) 4, 5, 6 и 16. Среднее арифметическое: (4+5+6+16) : 4 = 7,75.
Средние арифметические первых двух групп равны.
б) Попробуем составить группы так, чтобы их средние арифметические были равны.
Пример 1.
1) 1, 2, и 16. Среднее арифметическое
![]()
2) 3, 4, 8 и 9. Среднее арифметическое (3+4+8+9) : 4 = 6.
3) 5, 6 и 7. Среднее арифметическое: (5+6+7) : 3 = 6.
Нет, не получилось. А, может, так:
Пример 2.
1) 5 и 8. Среднее арифметическое (5+8) : 2 = 6,5
2) 6. Среднее арифметическое самого числа равно этому числу 6.
3) 1, 2, 3, 4, 7, 9 и 16. Среднее арифметическое: (1+2+3+4+7+9+16) : 7 = 6.
Опять не то. Или так:
Пример 3.
1) 6. Среднее арифметическое самого числа равно этому числу 6.
2) 3 и 9. Среднее арифметическое (3+9) : 2 = 6.
3) 1, 2, 4, 5, 7, 8 и 16. Среднее арифметическое:
![]()
Пример 4.
1) 4 и 8. Среднее арифметическое (4+8) : 2 = 6.
2) 3 и 9. Среднее арифметическое (3+9) : 2 = 6.
3) 1, 2, 5, 6, 7 и 16. Среднее арифметическое:
![]()
Не получается. Но мы заметили, что каждое из средних арифметических близко к среднему арифметическому всех десяти чисел:
(1+2+3+4+5+6+7+8+9+16) : 10 = 61 : 10 = 6,1. И если бы средние арифметические всех трёх групп были равны, то они были бы равны, именно, числу 6,1, но это невозможно, потому что: 1) сумма чисел в каждой группе выражается целым числом; 2) ни одну из сумм чисел в любой группе, не придется делить на 10, максимум на 7, как в примере 3.
Вывод: нет, одинаковыми все три значения средних арифметических быть не могут.
в) Примеры 1-4, рассмотренные в пункте б), позволяют понять непростой вопрос, на который нам предстоит ответить: «найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических».
Очевидно, что выбирать наименьшее придется
![]()
(смотрите примеры 1-4), так как наибольшие средние арифметические групп мы получим только если они будут максимально приближенными друг к другу, а именно: средние арифметические двух групп будут равны 6, а среднее арифметическое третьей группы будет больше шести. Понятно, что это третье число не может быть меньше или равно 6,1. Так как ни одна группа не может насчитывать больше 7-ми членов,



