Геометрия 10 класс | Профиль-математика

Рубрика "Геометрия 10 класс"

Задания на векторы в 1 части профильного ЕГЭ по математике

Задача. Даны векторы \( \vec{a}\ \)(2; 3) и \( \vec{b}\ \)(-3; b₀). Найдите b₀, если |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите меньшее из них.

Решение.

Модуль вектора \( \vec{a}\ \)(а₁; а₂) равен квадратному корню из суммы квадратов его координат:

\( | \vec{a}|=\sqrt{(a_1)^2+(a_2)^2}\ \);

\( | \vec{a}|=\sqrt{2^2+3^2}\ \); \( | \vec{a}|=\sqrt{13}\ \).

Найдём модуль вектора \( \vec{b}\ \)(-3; b₀).

\( | \vec{b}|=\sqrt{(-3)^2+(b_0)^2}\ \);

\( | \vec{b}|=\sqrt{9+(b_0)^2}\ \).

По условию |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.

Получаем b² = 2,25a².

9 + (b₀)² = 2,25 ∙ 13;

9 + (b₀)² = 29,25;

(b₀)² = 20,25;

b₀= ±4,5.

В ответе требуется записать меньшее из значений b₀.

Ответ: -4,5.

Задача. Даны векторы \( \vec{a}\ \)(4; -1) и \( \vec{b}\ \)(b₀; 8). Найдите b₀, если |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите большее из них.

Решение.

Найдём модуль вектора \( \vec{a}\ \)(4; -1).

\( | \vec{a}|=\sqrt{4^2+(-1)^2}\ \);

\( | \vec{a}|=\sqrt{17}\ \).

Найдём модуль вектора \( \vec{b}\ \)(b₀; 8).

\( | \vec{b}|=\sqrt{(b_0)^2+8^2}\ \);

\( | \vec{b}|=\sqrt{(b_0)^2+64}\ \);

По условию |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.

Получаем b² = 6,25a².

(b₀)² + 64 = 6,25 ∙ 17;

(b₀)² + 64 = 106,25;

(b₀)² = 42,25;

b₀= ±6,5.

В ответе требуется записать большее из значений b₀.

Ответ: 6,5.

Задача. Даны векторы \( \vec{a}(-1; 3)\ \), \( \vec{b}(4; 1)\ \), \( \vec{c}(2; c_0)\ \). Найдите с₀, если \( ( \vec{a}+\vec{b})\: \cdot \: \vec{c} =0\ \).

Решение.

Скалярное произведение векторов равно сумме произведение соответственных координат этих векторов.

3 ∙ 2 + 4 ∙ с₀ = 0;

с₀ = -6 : 4;

с₀ = -1,5.

Ответ: -1,5.

Задача. Даны векторы \( \vec{a}(3; -1)\ \), \( \vec{b}(2; 0)\ \), \( \vec{c}(4; c_0)\ \). Найдите с₀, если \( ( \vec{a}- \vec{b})\: \cdot \: \vec{c} =0\ \).

Решение аналогично решению предыдущей задачи.

1 ∙ 4 + (-1) ∙ с₀ = 0;

-с₀ = -4;

с₀ = 4.

Ответ: 4.

Задача. Даны векторы \( \vec{a}(-2; 4)\ \)и \( \vec{b}(2; -1)\ \). Известно, что векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправленные, а \( | \vec{c}|=| \vec{a}|\ \). Найдите х_с+у_с.

Решение.

Так как длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправлены, то и координаты вектора \( \vec{c}(x_c; y_c)\ \) больше координат вектора \( \vec{b}\ \) в два раза.

Получаем х_с = 2 ∙ 2 = 4 и у_с = -1 ∙ 2 = -2.

Тогда х_с + у_с = 4 + (-2) = 2.

Ответ: 2.

Задача. Даны векторы \( \vec{a}(4; -6)\ \)и \( \vec{b}(-2; 3)\ \). Известно, что \( | \vec{c}|=| \vec{a}|\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) противоположно направленные. Найдите х_с+у_с.

Решение аналогично решению предыдущей задачи.

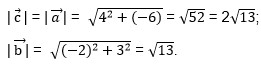
Длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \), по условию, противоположно направлены, следовательно отношение координат вектора \( \vec{c}(x_c; y_c)\ \) к соответственным координатам вектора \( \vec{b}\ \) равно (-2).

Получаем х_с = -2 ∙ (-2) = 4 и у_с = -2 ∙ 3 = -6.

Тогда х_с + у_с = 4 + (-6) = -2.

Ответ: -2.

Каждую из двух предыдущих задач можно решить быстро и легко графическим способом.

Смотрите видео.

Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}\ \), если \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). В ответ запишите сумму координат вектора \( \vec{c}\ \).

Решение.

Определим координаты данных векторов.

Каждая координата вектора равна разности соответствующих координат его конца и начала.

Смотрим рис. 2.

А₁(1; 2) и А₂(-5; 6); В₁(5; -4) и В₂(2; 4). Тогда

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

По условию \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). Следовательно,

Таким образом, сумма координат вектора \( \vec{c}\ \) равна 4,5.

Ответ: 4,5.

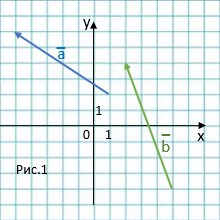
Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}(x_c; y_c)\ \), если \( \vec{c}=\vec{a}-1,5 \vec{b}\ \).

В ответ запишите произведение х_с ∙ у_с.

Решение аналогично решению предыдущей задачи.

Определим координаты данных векторов.

Смотрим рис. 4.

А₁(-7; -1) и А₂(5; 5); В₁(2; -4) и В₂(-6; 3). Тогда

По условию \( \vec{c}=\vec{a}-1,5 \vec{b}\ \). Следовательно,

Таким образом, искомое произведение координат вектора \( \vec{c}\ \)

х_с ∙ у_с = 24 ∙ (- 4,5) = -108.

Ответ: -108.

Задача. Даны векторы \( \vec{a}(4; y_a)\ \)и \( \vec{b}(x_b; 0)\ \), косинус угла между которыми равен \( \frac{2}{\sqrt{5}}\ \). Найдите у_а. Если таких значений несколько, в ответ запишите большее из них.

Решение.

Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла φ между ними.

В прямоугольной системе координат скалярное произведение векторов

\( \vec{a}(x_1; y_1)\ \)и \( \vec{b}(x_2; y_2)\ \) выражается формулой

\( \vec{a} \cdot \vec{b} =x_1x_2+y_1y_2\ \)

Получаем равенство:

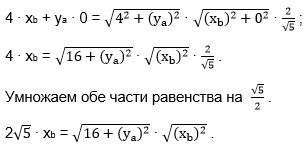
Возведём обе части равенства в квадрат:

20 ∙ (x_b)² = (16 + (y_a)²) ∙ (x_b)²; делим на (x_b)² обе части равенства:

20 = 16 + (у_а)²;

(у_а)² = 4;

у_а = ±2.

Большее из этих значений у_а = 2.

Ответ: 2.

Задача. Даны векторы \( \vec{a}(x_a; -2)\ \)и \( \vec{b}(0; y_b)\ \), косинус угла между которыми равен \( -\sqrt{0,2}\ \). Найдите x_а. Если таких значений несколько, в ответ запишите меньшее из них.

Решение аналогично решению предыдущей задачи.

Составим равенство на основании формулы:

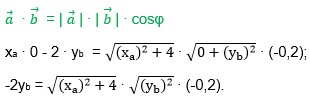
Разделим обе части равенства на (-0,2).

Возведём обе части равенства в квадрат:

20 ∙ (у_b)² = ((х_a)² + 4) ∙ (у_b)²; делим на (у_b)² обе части равенства:

20 = (х_а)² + 4;

(х_а)² = 16;

х_а = ±4.

Меньшее из этих значений х_а = -4.

Ответ: -4.

Задача. Даны векторы \( \vec{a}(14; -2)\ \)и \( \vec{b}(-7; -1)\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).

Решение.

Найдём модули данных векторов.

Получаем:

14 ∙ (-7) + (-2) ∙ (-1) = 10 ∙ 5 ∙ cosα;

-98 + 2 = 100 ∙ cosα, отсюда cosα = -0,96.

Ответ: -0,96.

Задача. Даны векторы \( \vec{a}(-6; 2)\ \)и \( \vec{b}(9; 13)\ \). Найдите косинус угла между

векторами \( \vec{a}\ \)и \( \vec{b}\ \).

Решение аналогично решению предыдущей задачи.

Находим модули данных векторов.

Получаем:

-6 ∙ 9 + 2 ∙ 13 = 2 ∙ 5 ∙ cosα;

-54 + 26 = 100 ∙ cosα;

-28 = 100 ∙ cosα;

отсюда cosα = -0,28.

Ответ: -0,28.

Как найти скалярное произведение векторов

Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите скалярное произведение векторов \( \vec{a}\ \)и \( 2\vec{b}\ \).

Решение.

Скалярным произведением векторов

\( \vec{a}\ \){a₁; a₂} и \( \vec{b}\ \){b₁; b₂}

называется число a₁b₁ + a₂b₂.

Произведением вектора \( \vec{a}\ \){a₁; a₂} на число λ называется вектор \( λ\vec{a}\ \){λa₁; λa₂}.

Пусть вектор \( \vec{a}\ \)имеет началом точку

А₁(х₁; у₁), а концом – точку А₂(х₂; у₂).

Координатами вектора \( \vec{a}\ \) будем называть числа а₁= х₂-х₁, а₂= у₂-у₁.

У нас (см. рис.2) А₁(-2; 5), А₂(-6; -4).

Тогда \( \vec{a}(-4; -9)\ \).

Так как В₁(6; 2), В₂(1; -2), то \( \vec{b}\ \){-5; -4}.

Следовательно, \( 2\vec{b}(-10; -8)\ \).

Итак, искомое скалярное произведение

\( \vec{a}\ \)и \( 2\vec{b}\ \):

\( \vec{a}\ \)∙ \( 2\vec{b}\ \)= -4 ∙ (-10) + (-9) ∙ (-8) = 40 + 72 = 112.

Ответ: 112.

Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите скалярное произведение векторов \( 2\vec{a}\ \)и \( \vec{b}\ \).

Решение.

У нас (см. рис.4) А₁(-6; 4), А₂(-2; -2).

Тогда \( \vec{a}\ \){4; -6} и \( 2\vec{a}\ \){8; -12}.

Начало и конец вектора \( \vec{b}\ \) – точки В₁(-1; -4) и В₂(2; 3),

следовательно, \( \vec{b}\ \){3; 7}.

Итак, искомое скалярное произведение

\( 2\vec{a}\ \)и \( \vec{b}\ \):

\( 2\vec{a}\ \)∙ \( \vec{b}\ \)= 8 ∙ 3 + (-12) ∙ 7 = 24 -84 = -60.

Ответ: -60.

Задача. Даны векторы \( \vec{a}\ \)(2; -5) и \( \vec{b}\ \)(5; 7). Найдите скалярное произведение векторов \( 0,6\vec{a}\ \)и \(1,4\vec{b}\ \).

Решение.

\( 0,6\vec{a}\ \)(0,6 ∙ 2; 0,6 ∙ (-5)); \( 0,6\vec{a}\ \)(1,2; -3).

\( 1,4\vec{b}\ \)(1,4 ∙ 5; 1,4 ∙ 7); \( 1,4\vec{b}\ \)(7; 9,8).

Скалярное произведение этих векторов

\( 0,6\vec{a}\ \)∙ \(1,4\vec{b}\ \) = 1,2 ∙ 7 + (-3) ∙ 9,8 = 8,4 -29,4 = -21.

Ответ: -21.

Задача. Даны векторы \( \vec{a}\ \)(2,2; -4) и

\( \vec{b}\ \)(-1,25; -1). Найдите скалярное произведение векторов \( 3\vec{a}\ \)и \(4\vec{b}\ \).

Решение.

Искомое скалярное произведение векторов

\( 3\vec{a}\ \)∙ \(4\vec{b}\ \) = 12\( \vec{a}\ \)∙ \( \vec{b}\ \) = 12(2,2 ∙ (-1,25) + (-4) ∙ (-1)) =

= 12(-2,75 + 4) = 12 ∙ 1,25 = 15.

Ответ: 15.

Задача. На координатной плоскости (рис.5) изображены векторы \( \vec{a}\ \), \( \vec{b}\ \)и \( \vec{c}\ \). Найдите скалярное произведение \( \vec{a}\ \)∙ \( (\vec{b}+\vec{c})\ \).

Решение.

Мы знаем, что скалярное произведение двух векторов равно сумме произведений соответственных координат этих координат.

Сумму векторов \( \vec{b}\ \) и \( \vec{c}\ \) заменим вектором \( \vec{d}\ \).

Найдём координаты векторов \( \vec{a}\ \)и \( \vec{d}\ \).

Смотрим рис. 6.

А₁(-1; -2) и А₂(-7; 3). Тогда \( \vec{a}\ \){-6; 5}.

B₁(5; -4) и B₂(5; 1). Тогда \( \vec{b}\ \){0; 5}.

C₁(1; 4) и C₂(-6; -1). Тогда \( \vec{c}\ \){-7; -5}.

При сложении двух векторов, складываются соответственные координаты этих векторов.

Так как \( \vec{d}\ \)= \( \vec{b}\ \)+\( \vec{c}\ \), то \( \vec{d}\ \){-7; 0}. Тогда искомое скалярное произведение:

\( \vec{a}\ \)∙ \( ( \vec{b}+\vec{c})\ \)= \( \vec{a}\ \)∙ \( \vec{d}\ \) = -6 ∙ (-7) + 5 ∙ 0 = 42.

Ответ: 42.

Задача. На координатной плоскости (рис.7) изображены векторы \( \vec{a}\ \), \( \vec{b}\ \)и \( \vec{c}\ \). Найдите скалярное произведение \( \vec{a}\ \)∙ \( (3 \vec{a}- 2 \vec{b})\ \).

Решение.

Применим распределительный закон умножения векторов.

\( \vec{a}\ \)∙ \( (3 \vec{b}- 2 \vec{c})\ \)= \( 3\vec{a}\ \) ∙ \( \vec{b}\ \)- \( 2\vec{a}\ \) ∙ \( \vec{c}\ \).

Найдём скалярные произведения векторов: \( \vec{a}\ \)и \( \vec{b}\ \); \( \vec{a}\ \)и \( \vec{c}\ \).

Определим координаты всех трёх векторов.

Смотрим рисунок 8.

А₁(-2; -1) и А₂(-7; 3). Тогда \( \vec{a}\ \){-5; 4}.

B₁(3; -1) и B₂(6; 4). Тогда \( \vec{b}\ \){3; 5}.

C₁(2; 5) и C₂(-2; 2). Тогда \( \vec{c}\ \){-4; -3}.

Тогда

\( \vec{a}\ \)∙ \( \vec{b}\ \)= -5 ∙ 3 + 4 ∙ 5 = -15 + 20 = 5;

\( \vec{a}\ \)∙ \( \vec{c}\ \)= -5 ∙ (-4) + 4 ∙ (-3) = 20 -12 = 8.

Искомое скалярное произведение векторов

\( \vec{a}\ \)∙ \( (3 \vec{b}- 2 \vec{c})\ \)= \( 3\vec{a}\ \) ∙ \( \vec{b}\ \)- \( 2\vec{a}\ \) ∙ \( \vec{c}\ \)= 3 ∙ 5 -2 ∙ 8 = 15 -16 = -1.

Ответ: -1.

Задача. Вычислите скалярное произведение векторов \( \vec{a}\ \) и \( \vec{b}\ \),

если |\( \vec{a}\ \)| = 3, |\( \vec{b}\ \)| = 4, а угол между ними равен 60°.

Решение.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

\( \vec{a}\ \) ∙ \( \vec{b}\ \)= |\( \vec{a}\ \)| ∙ |\( \vec{b}\ \)| ∙ cosφ,

где φ – угол между векторами \( \vec{a}\ \) и \( \vec{a}\ \).

Получаем

\( \vec{a}\ \) ∙ \( \vec{b}\ \)= 3 ∙ 4 ∙ cos60° = 12 ∙ 0,5 = 6.

Ответ: 6.

Задача. Вычислите скалярное произведение векторов

\( \vec{p}\ \) = \( \vec{a}\ \)- \( \vec{b}\ \)- \( \vec{c}\ \) и \( \vec{q}\ \) = \( \vec{a}\ \)- \( \vec{b}\ \)+\( \vec{c}\ \),

если |\( \vec{a}\ \)| = 5, |\( \vec{b}\ \)| = 2, |\( \vec{c}\ \)| = 4 и \( \vec{a} \perp \vec{b}\ \).

Решение.

\( \vec{p}\ \) ∙ \( \vec{q}\ \)= (\( \vec{a}\ \)- \( \vec{b}\ \)-\( \vec{c}\ \)) ∙ (\( \vec{a}\ \)- \( \vec{b}\ \)+\( \vec{c}\ \))=

= \( \vec{a}\ \)²-\( \vec{a}\ \)∙ \( \vec{b}\ \)-\( \vec{a}\ \)∙ \( \vec{c}\ \)-\( \vec{a}\ \) ∙ \( \vec{b}\ \)+\( \vec{b}\ \)²+\( \vec{b}\ \) ∙ \( \vec{c}\ \)+\( \vec{a}\ \) ∙ \( \vec{c}\ \)-\( \vec{b}\ \) ∙ \( \vec{c}\ \)-\( \vec{c}\ \)² =

= |\( \vec{a}\ \)|²+|\( \vec{b}\ \)|²-|\( \vec{c}\ \)|²-\(2 \vec{a}\ \)∙ \( \vec{b}\ \)= 5² + 2² -4² -0 =

= 25 + 4 -16 = 13.

Скалярное произведение двух взаимно перпендикулярных векторов равно нулю.

Так как у нас по условию \( \vec{a} \perp \vec{b}\ \), то \( \vec{a}\ \) ∙ \( \vec{b}\ \)= 0.

Ответ: 13.

Задача. Вычислите скалярное произведение векторов \( \vec{a}\ \)и \( \vec{b}\ \),

если \( \vec{a}\ \)= 3\( \vec{p}\ \) -2\( \vec{q}\ \) и \( \vec{b}\ \)= \( \vec{p}\ \)+ 4\( \vec{q}\ \), где \( \vec{p}\ \)и \( \vec{q}\ \) – единичные взаимно перпендикулярные векторы.

Решение.

\( \vec{a}\ \)∙ \( \vec{b}\ \)= (3\( \vec{p}\ \) -2\( \vec{q}\ \))(\( \vec{p}\ \)+ 4\( \vec{q}\ \)) = 3\( \vec{p}\ \)² -2\( \vec{p}\ \)∙ \( \vec{q}\ \)+ 12\( \vec{p}\ \)∙ \( \vec{q}\ \) -8\( \vec{q}\ \)² =

= 3|\( \vec{p}\ \)|² +10\( \vec{p}\ \)∙ \( \vec{q}\ \) -8|\( \vec{q}\ \)|² = 3 ∙ 1 + 10 · 0 -8 ∙ 1 = -5.

Ответ: -5.

Задача. Даны точки А(1; 3; 0), B(2; 3; -1),

C(1; 2; -1). Найдите скалярное произведение

векторов \( \vec{AB}\ \) и \( \vec{AC}\ \).

Решение.

Так как скалярное произведение векторов равно сумме произведений соответственных координат этих векторов, то найдём эти координаты.

\( \vec{AB}\ \){2-1; 3-3; -1-0} → \( \vec{AB}\ \){1; 0; -1};

\( \vec{AC}\ \){1-1; 2-3; -1-0} → \( \vec{AC}\ \){0; -1; -1}.

\( \vec{AB}\ \) ∙ \( \vec{AC}\ \) = 1 ∙ 0 + 0 ∙ (-1) + (-1) ∙ (-1) = 1.

Ответ: 1.

Как найти косинус угла между векторами, изображёнными на координатной плоскости

Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите cosα,

где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).

1 способ решения – традиционный.

Применим формулу \( cos \alpha=\frac{ \vec{a}\: \cdot\: \vec{b}}{| \vec{a}|\: \cdot\:| \vec{b}|}\ \) ( * )

Здесь \( \vec{a}\: \cdot\: \vec{b}\ \)- скалярное произведение векторов \( \vec{a}\ \)и \( \vec{b}\ \), которое равно сумме произведений соответственных координат этих векторов.

Требуется найти координаты и модули данных векторов.

Для вектора \( \vec{a}\ \)координаты начала А₁(-1; -4) и конца А₂(-4; 2).

Тогда абсцисса вектора \( \vec{a}\ \)равна -4-(-1) = -3; ордината 2-(-4) = 6.

Вектор \( \vec{a}\ \){-3; 6}, модуль вектора \( \vec{a}\ \):

\( | \vec{a}|=\sqrt{(-3)^2+6^2}\ \)= \( \sqrt{9+36}\ \)= \( \sqrt{45}\ \)= \( 3\sqrt{5}\ \).

Для вектора \( \vec{b}\ \)координаты начала В₁(-3; 5) и конца В₂(5; 1).

Тогда абсцисса вектора \( \vec{b}\ \) равна 5-(-3) = 8; ордината 1-5 = -4.

Вектор \( \vec{b}\ \){8; -4}, модуль вектора \( \vec{b}\ \):

\( | \vec{b}|=\sqrt{8^2+(-4)^2}\ \)= \( \sqrt{64+16}\ \)= \( \sqrt{80}\ \)= \( 4\sqrt{5}\ \).

Все найденные значения подставляем в формулу ( * ):

\( cos \alpha=\frac{-3\: \cdot\:8\:+\:6\: \cdot\:(-4)}{3\sqrt{5}\ \cdot \:4\sqrt{5}}\ \);

\( cos \alpha=\frac{-48}{12\: \cdot\:5 }\ \);

\( cos \alpha=-\frac{4}{5}\ \);

cosα = -0,8.

Ответ: -0,8.

2 способ решения – нас не будут интересовать координаты векторов.

Выберем точку с целыми координатами на векторе \( \vec{a}\ \).

Пусть это будет точка М(-3; 0). Отложим от этой точки вектор \( \vec{MN}\ \), сонаправленный вектору \( \vec{b}\ \) так, чтобы точка N имела целые координаты. Достроим треугольник АМN.

Сторона АМ этого треугольника – это гипотенуза прямоугольного треугольника с катетами 2 и 1.

АМ² = 2² + 1² = 4 + 1= 5;

\( AM=\sqrt{5}\ \).

Сторона МN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 4 и 2.

МN² = 4² + 2² = 16 + 4 = 20;

\( MN=\sqrt{20}\ \) или \( MN=2\sqrt{5}\ \).

Сторона АN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 5 и 4.

АN² = 5² + 4² = 25 + 16 = 41;

\( AN=\sqrt{41}\ \).

Искомый угол АМТ обозначим через α

На основании теоремы косинусов

\( cos \alpha=\frac{AM^2+MN^2-AN^2}{2 \cdot AM\: \cdot\:MN}\ \);

\( cos \alpha=\frac{5+20-41}{2\sqrt{5}\: \cdot\:2\sqrt{5}}\ \);

\( cos \alpha=-\frac{16}{4\: \cdot\:5 }\ \);

\( cos \alpha=-\frac{4}{5}\ \);

cosα = -0,8.

Ответ: -0,8.

Ещё одна задача.

Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).

Смотрим видео.

На координатной плоскости изображены векторы а, b и с

Задача. На координатной плоскости изображены векторы

Решение.

Пусть А₁(-7; 6) и А₂(-3; 3) – начало и конец

Пусть В₁(2; 1) и В₂(2; 5) – начало и конец

Пусть C₁(4; -4) и C₂(-4; -2) – начало и конец

Ответ: 5.

Эту задачу на сложение данных векторов можно решить графически, используя правило многоугольника. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.

Длина (модуль) этого вектора равна 5. Это гипотенуза прямоугольного треугольника с катетами 3 и 4.

Ответ: 5.

Смотрим видео.

Задача. На координатной плоскости изображены векторы

Смотрим видео.

Основание пирамиды SABC — равносторонний треугольник

Задача. Основание пирамиды SABC — равносторонний треугольник АВС. Боковое ребро SA перпендикулярно плоскости основания, точки М и N — середины рёбер ВС и АВ соответственно, причём SN=AM.

а) Докажите, что угол между прямыми АМ и SN равен 60°.

б) Найдите расстояние между этими прямыми,

Решение.

а) Докажем, что угол между прямыми АМ и SN равен 60°. Прямые АМ и SN являются скрещивающимися.

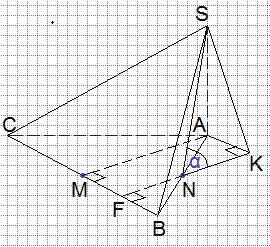Углом между скрещивающимися прямыми считают угол между соответственно параллельными им пересекающимися прямыми.

Прямую АМ заменим параллельной ей прямой FN. Углом между скрещивающимися прямыми АМ и SN будет угол между пересекающимися прямыми FN и SN. Обозначим этот угол через α и докажем, что он равен 60°.

Проведём АК параллельно ВС. Соединим точки S и К. Так как точка М – середина ВС, а треугольник АВС равносторонний, то АМ – медиана, высота и биссектриса треугольника АВС. Тогда прямая FK, параллельная АМ будет также перпендикулярна ВС. А так как АК параллельна ВС, то АК перпендикулярна и АМ, и FK. Таким образом, четырёхугольник АМFК является прямоугольником. Прямая SК является наклонной к плоскости АВС, SА – перпендикуляр к плоскости АВС, АК – проекция прямой SК на плоскость АВС. Прямая FK, проведённая через основание наклонной SК перпендикулярно её проекции АК, будет перпендикулярна наклонной SК на основании теоремы о трёх перпендикулярах. Значит, треугольник SNK является прямоугольным с прямым углом при вершине К. Катет NK равен половине FK, а значит, и половине АМ (противоположные стороны прямоугольника АМFК равны, а равенство отрезков FN и NK следует из равенства прямоугольных треугольников NFB и NKA по равным катетам BN и AN и вертикальным углам при вершине N).

По условию SN=AM , поэтому

Итак, из прямоугольного треугольника SNK

Отсюда следует:

что и требовалось доказать.

б) Найдём расстояние между скрещивающимися прямыми АМ и SN. Используем метод проекций, опирающийся на следующую лемму.

Лемма Шарыгина И.Ф.

Расстояние между скрещивающимися прямыми равно расстоянию от точки, являющейся проекцией одной из прямых на перпендикулярную ей плоскость, до проекции другой прямой на эту плоскость.

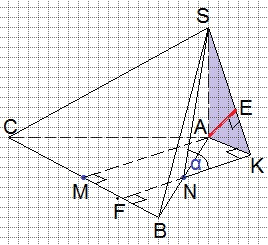У нас SKA – плоскость, перпендикулярная прямой АМ (АМ перпендикулярна SA по условию и АК по построению). А – проекция АМ на плоскость SKA. SN – наклонная к плоскости SKA, NK – перпендикуляр, SК – проекция наклонной SN к плоскости SKA. Расстояние от точки А до SК и будет являться искомым расстоянием между скрещивающимися прямыми АМ и SN. Проведём АЕ перпендикулярно SК. Отрезок АЕ – это высота прямоугольного треугольника SKA, проведённая к гипотенузе SK.

В равностороннем треугольнике АВС

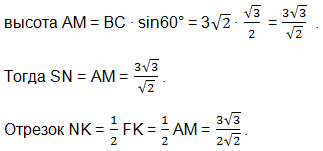
Так как в треугольнике АВМ точка N – середина стороны АВ, FN параллельна АМ, поэтому FN – средняя линия треугольника АВМ. Точка F – середина отрезка ВМ.