Найдите все значения а, при каждом из которых функция

Задача. Найдите все значения а, при каждом из которых функция

f(x) = x²-3|x-a²|-5x

имеет более двух точек экстремума.

Решение. Экстремум (минимум или максимум) функции возможен в точке, в которой производная функции меняет знак. Раскроем модульные скобки.

1) Случай. Пусть х-а² ≥ 0   →   х  ≥ а². Получаем f(x) = x²-3x + 3a²-5x;

f(x) = x²-8x + 3a². Находим производную. f ’(x) = 2x-8 = 2(x-4). Критическая точка х = 4. Производная в точке х = 4 меняет знак с «-» на «+». Следовательно, в точке х = 4 функция f(x) = x²-8x + 3a² имеет минимум.

Найдём значение функции в точке х = 4.

f(4) = 4²-8 ∙ 4 + 3a² = 3a²-16.

Итак, x_min = 4;  f_min = 3a²-16.

2) Случай. Пусть х-а² < 0   →   х  < а². Получаем f(x) = x² + 3x-3a²-5x;

f(x) = x²-2x-3a². Находим производную.

f ’(x) = 2x-2 = 2(x-1). Критическая точка х = 1. Производная в точке х = 1 меняет знак с «-» на «+». Следовательно, в точке

х = 1 функция f(x) = x²-2x-3a² имеет минимум.

Найдём значение функции в точке х = 1.

f(1) = 1²-2 ∙ 1-3a² = -1-3a².

Итак, x_min = 1;  f_min =  -1-3a².

Чтобы изобразить функции графически в каждом из двух рассмотренных случаев нам нужно определиться со значением числа а².

Возможны три варианта расположения числа а².

Вариант 1.

а² < 1 < 4. Для определённости возьмём а² = 0.

Функция f(x) = x²-8x + 3a² имеет x_min = 4;  f_min = 3a²-16 = -16.

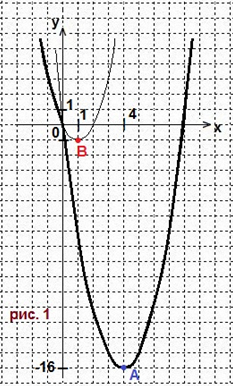
Строим параболу f(x) = x²-8x + 3a², вершина которой A(4; -16).

Так как функцию f(x) = x²-8x + 3a²  мы получили при условии,

что х  ≥ а², то надо взять точки параболы, удовлетворяющие условию х ≥ 0.

Функция f(x) = x²-2x-3a² имеет

x_min = 1;  f_min = -1-3a²= -1.

Строим параболу f(x) = x²-2x-3a² с вершиной В(1; -1).

Так как функцию f(x) = x²-2x-3a² мы получили при условии, что х  < а², то надо взять точки параболы, удовлетворяющие условию     х < 0.

Смотрите рис.1. Получается только 1 экстремум.

Вывод: вариант 1 не подойдёт.

Вариант 2.

1 < а² < 4. Для определённости возьмём а² = 3.

Функция f(x) = x²-8x + 3a² имеет x_min = 4;  f_min = 3a²-16 = 3 ∙ 3-16 = -7.

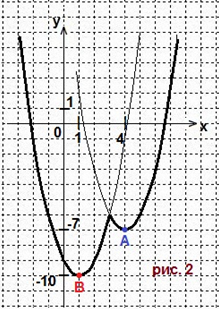
Строим параболу f(x) = x²-8x + 3a², вершина которой A(4; -7).

Так как функцию f(x) = x²-8x + 3a²  мы получили при условии,

что х  ≥ а², то надо взять точки параболы, удовлетворяющие условию х ≥ 3.

Функция f(x) = x²-2x-3a² имеет x_min = 1;  f_min = -1-3a²= -1-3 ∙ 3 = -10.

Строим параболу f(x) = x²-2x-3a² с вершиной В(1; -10).

Так как функцию f(x) = x²-2x-3a² мы получили при условии, что х  < а², то надо взять точки параболы, удовлетворяющие условию х < 3. Смотрите рис.2. Получается 3 экстремума.

Вывод: вариант 2 (1 < а² < 4 ) подходит. Найдём значение а, решив систему неравенств:

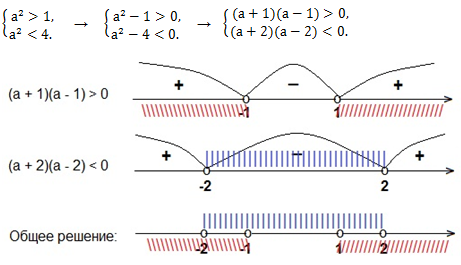
Получаем а  (-2; -1)  (1; 2).

Вариант 3.

1 < 4 < а².

Для определённости возьмём а² = 5.

Функция f(x) = x²-8x + 3a² имеет

x_min = 4;  f_min = 3a²-16 = 3 ∙ 5-16 = -1.

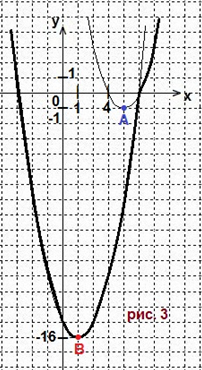
Строим параболу f(x) = x²-8x + 3a², вершина которой A(4; -1).

Так как функцию f(x) = x²-8x + 3a²  мы получили при условии, что х  ≥ а², то надо взять точки параболы, удовлетворяющие условию х ≥ 5.

Функция f(x) = x²-2x-3a² имеет

x_min = 1;  f_min = -1-3a²= -1-3 ∙ 5 = -16.

Строим параболу f(x) = x²-2x-3a² с вершиной В(1; -16).

Так как функцию f(x) = x²-2x-3a² мы получили при условии, что х  < а², то надо взять точки параболы, удовлетворяющие условию х < 5.

Смотрите рис.3. Получается только 1 экстремум. Вывод: вариант 3 не подойдёт.

Ответ: а  (-2; -1)  (1; 2).