В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей.

Задача. В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей. Условия его возврата таковы:

-в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;

-в период с февраля по сентябрь необходимо выплатить часть долга;

-в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же величину Q рублей меньше долга на октябрь предыдущего года;

-в 2033 и 2034 годах выплаты по кредиту равны;

-к октябрю 2034 года кредит должен быть полностью погашен.

Найдите величину Q, если общая сумма выплат по кредиту должна составить 4168 тыс. рублей.

Решение.

Пусть ежегодно в первые 5 лет долг будет уменьшаться на Q тыс. рублей (не рублей, а тысяч рублей). Посчитаем сумму процентов, которые будут выплачены за эти 5 лет:

0,15 ∙ (2560 + (2560-Q) + (2560-2Q) + (2560-3Q) + (2560-4Q)) =

= 0,15 ∙ (5 ∙ 2560-10Q) = (1920-1,5Q) тыс. рублей.

Следовательно, за первые 5 лет общие выплаты составят

5Q + 1920-1,5Q = (3,5Q + 1920) тыс. рублей. Остаток долга станет равным

(2560-5Q) тыс. рублей (ежегодно будут списывать только Q тыс. рублей).

Обозначим эту сумму (остаток долга) через S.

S = 2560-5Q. Эта сумма будет выплачена в 2033 и 2034 годах двумя равными платежами – обозначим каждый такой платёж через Y. Как это будет происходить?

Банк увеличит сумму долга на 15% — получится 115% от S, т.е 1,15S.

Клиент платит Y тыс. рублей, и долг станет равным (1,15S-Y) тыс. рублей.

Банк начисляет на эту сумму 15% — долг составит 1,15(1,15S-Y).

Клиент выплачивает Y тыс. рублей, и долг обнулится, т.е. мы имеем равенство:

1,15 ∙ (1,15S -Y)-Y = 0.

1,15² ∙ S -1,15Y-Y = 0

1,3225S -1,15Y -Y = 0

2,15Y = 1,3225S.

А так как S = (2560-5Q), то 2,15Y = 1,3225(2560-5Q). Выразим Y.

Так как  Y – это платёж в каждый из двух последних лет кредитования, то за 2 последних года банку будет выплачено 2Y тыс. рублей.

Общие выплаты за все 7 лет составят:

3,5Q + 1920 + 2Y или 4168 тыс. рублей.

3,5Q + 1920 + 2Y = 4168;

3,5Q + 2Y = 4168-1920;

3,5Q + 2Y = 2248;

Подставим вместо Y его значение и решим уравнение относительно Q.

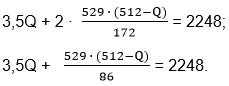
Умножаем обе части равенства на 86.

301Q + 529(512-Q) = 193328;

301Q + 270848 -529Q = 193328;

301Q -529Q = 193328 -270848;

-228Q = -77520;

Q = 340. Мы нашли Q в тысячах рублей, ответ нужно дать в рублях.

Ответ: 340000 рублей.