В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы: каждый январь долг увеличивается на 10%
Задача. В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:
-каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
-с февраля по июнь необходимо выплатить одним платежом часть долга;
-в июле 2026, 2027, 2028, 2029 и 2030 долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
-в июле 2030 года долг должен составлять 800 тысяч рублей;
-в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же сумму меньше долга на июль предыдущего года;
Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.
Решение. Пусть в каждый из первых пяти лет долг будет уменьшаться на х тыс. рублей. Так как через эти 5 лет долг должен составлять 800 тыс. рублей, то первоначальный кредит равен (5х+800). С этой суммы посчитаем все проценты, которые будут начислены банком в первые 5 лет:
0,1(5х+800 + 4х+800 + 3х+800 + 2х+800 + х+800) =
= 0,1 ∙ 15х + 0,1 ∙ 800 ∙ 5 = 1,5х + 400 (тыс. руб.).
С июля 2030 года долг должен составлять 800 тысяч рублей по условию. Погашать его нужно будет следующие 5 лет на одну и ту же сумму. Мы легко определим эту сумму. Делим 800 на 5 и получаем 160 тысяч рублей. Однако, для удобства подсчёта процентов за последние 5 лет, обозначим эту сумму через у. Итак,
у=160, значит, долг 800=5у. Считаем проценты:
0,1(5у+4у+3у+2у+у) = 0,1 ∙ 15у = 1,5у.
Заменяем у на 160 и получаем 1,5 ∙ 160 = 240 тысяч рублей – проценты за последние 5 лет.
Таким образом, за всё время кредитования клиент выплатит:
(5х + 800) тыс. руб. — данную банком сумму;
(1,5х + 400) тыс. руб. — проценты за первые 5 лет;
240 тыс. руб. — проценты за последние 5 лет.
По условию сумма выплат по кредиту равна 2090 тысяч рублей. Получаем уравнение:
5х + 800 + 1,5х + 400 + 240 = 2090. Решаем:
6,5х = 2090-1440;
6,5х = 650;
х = 100.
На 100 тыс. руб. будет уменьшаться долг ежегодно в первые 5 лет.
А так как взятую сумму кредита мы обозначали через (5х+800) тысяч рублей, то она составит 5 ∙ 100 + 800 = 1300 тысяч рублей.
Ответ: 1300000 рублей.
15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы: 1-го числа каждого месяца долг возрастает на 3%
Задача. 15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
Решение. Для удобства обозначим через х величину, на которую ежемесячно уменьшался долг первые 10 месяцев (х = 80 тыс. рублей), а через у – остаток долга на 11 месяц кредитования (долг 15 числа 10-го месяца). Тогда, очевидно, что кредит был равен (10х + у) тысяч рублей.
Подсчитаем проценты за первые 10 месяцев.
0,03 ∙ ( (10х+у) + (9х+у) + (8х+у) + … + (х+у)) =
= 0,03 ∙ (10х + 9х + 8х +…+ х) + 0,03 ∙ 10у =
= 0,03 ∙ 55х + 0,3у = 1,65х + 0,3у.
За 11-й месяц будет выплачено (у + 0,03у) тыс. рублей.
Итак, за всё время кредитования клиент заплатил
10х + 1,65х + 0,3у + у + 0,03у или 1198 тыс. рублей.
10х – это 80 ∙ 10 = 800 тысяч рублей.
800 + 1,65х + 1,33у = 1198;
1,65 ∙ 80 + 1,33у = 1198-800;
132 + 1,33у = 398;
1,33у = 398-132;
1,33у = 266;
у = 200.
Ответ: 200 тысяч рублей.
В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей.
Задача. В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей. Условия его возврата таковы:
-в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
-в период с февраля по сентябрь необходимо выплатить часть долга;
-в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же величину Q рублей меньше долга на октябрь предыдущего года;
-в 2033 и 2034 годах выплаты по кредиту равны;
-к октябрю 2034 года кредит должен быть полностью погашен.
Найдите величину Q, если общая сумма выплат по кредиту должна составить 4168 тыс. рублей.
Решение.
Пусть ежегодно в первые 5 лет долг будет уменьшаться на Q тыс. рублей (не рублей, а тысяч рублей). Посчитаем сумму процентов, которые будут выплачены за эти 5 лет:
0,15 ∙ (2560 + (2560-Q) + (2560-2Q) + (2560-3Q) + (2560-4Q)) =
= 0,15 ∙ (5 ∙ 2560-10Q) = (1920-1,5Q) тыс. рублей.
Следовательно, за первые 5 лет общие выплаты составят
5Q + 1920-1,5Q = (3,5Q + 1920) тыс. рублей. Остаток долга станет равным
(2560-5Q) тыс. рублей (ежегодно будут списывать только Q тыс. рублей).
Обозначим эту сумму (остаток долга) через S.
S = 2560-5Q. Эта сумма будет выплачена в 2033 и 2034 годах двумя равными платежами – обозначим каждый такой платёж через Y. Как это будет происходить?
Банк увеличит сумму долга на 15% — получится 115% от S, т.е 1,15S.
Клиент платит Y тыс. рублей, и долг станет равным (1,15S-Y) тыс. рублей.
Банк начисляет на эту сумму 15% — долг составит 1,15(1,15S-Y).
Клиент выплачивает Y тыс. рублей, и долг обнулится, т.е. мы имеем равенство:
1,15 ∙ (1,15S -Y)-Y = 0.
1,152 ∙ S -1,15Y-Y = 0
1,3225S -1,15Y -Y = 0
2,15Y = 1,3225S.
А так как S = (2560-5Q), то 2,15Y = 1,3225(2560-5Q). Выразим Y.
Так как Y – это платёж в каждый из двух последних лет кредитования, то за 2 последних года банку будет выплачено 2Y тыс. рублей.
Общие выплаты за все 7 лет составят:
3,5Q + 1920 + 2Y или 4168 тыс. рублей.
3,5Q + 1920 + 2Y = 4168;
3,5Q + 2Y = 4168-1920;
3,5Q + 2Y = 2248;
Подставим вместо Y его значение и решим уравнение относительно Q.
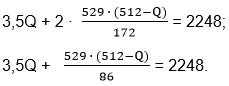
Умножаем обе части равенства на 86.
301Q + 529(512-Q) = 193328;
301Q + 270848 -529Q = 193328;
301Q -529Q = 193328 -270848;
-228Q = -77520;
Q = 340. Мы нашли Q в тысячах рублей, ответ нужно дать в рублях.
Ответ: 340000 рублей.
В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей.
Задача. В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей. Условия его возврата таковы:
-в январе каждого года действия кредита долг увеличивается на 10% от суммы долга на конец предыдущего года;
-в период с февраля по сентябрь необходимо выплатить часть долга;
-в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же сумму меньше долга на октябрь предыдущего года;
-в 2033 и 2034 годах выплаты по кредиту равны;
-к октябрю 2034 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат по кредиту должна составить 6025 тыс. рублей. Сколько рублей составит выплата 2031 года?
Решение.
Пусть ежегодно в первые 5 лет долг будет уменьшаться на х тыс. рублей. Посчитаем сумму процентов, которые будут выплачены за эти 5 лет:
0,1 ∙ (4350 + (4350-х) + (4350-2х) + (4350-3х) + (4350-4х)) =
= 0,1 ∙ (5 ∙ 4350-10х) = (2175-х) тыс. рублей.
Следовательно, за первые 5 лет общие выплаты составят
5х + 2175-х = (4х + 2175) тыс. рублей. Остаток долга станет равным
(4350-5х) тыс. рублей (ежегодно будут списывать только х тыс. рублей).
Обозначим эту сумму (остаток долга) через S.
S = 4350-5x. Эта сумма будет выплачена в 2033 и 2034 годах двумя равными платежами – обозначим каждый такой платёж через Y. Как это будет происходить?
Банк увеличит сумму долга на 10% — получится 110% от S, т.е 1,1S.
Клиент платит Y тыс. рублей, и долг станет равным (1,1S-Y) тыс. рублей.
Банк начисляет на эту сумму 10% — долг составит 1,1(1,1S-Y).
Клиент выплачивает Y тыс. рублей, и долг обнулится, т.е. мы имеем равенство:
1,1 ∙ (1,1S -Y)-Y = 0.
1,12 ∙ S -1,1Y-Y = 0
1,21S -1,1Y -Y = 0
2,1Y = 1,21S.
А так как S = (4350-5х), то 2,1Y = 1,21(4350-5x). Выразим Y.
Так как Y – это платёж в каждый из двух последних лет кредитования, то за 2 последних года банку будет выплачено 2Y тыс. рублей.
Общие выплаты за все 7 лет составят:
4х + 2175 + 2Y или 6025 тыс. рублей.
4х + 2175 + 2Y = 6025;
4х + 2Y = 6025-2175;
4х + 2Y = 3850;
2х + Y = 1925.
Подставим вместо Y его значение и решим уравнение относительно х.
Умножаем обе части равенства на 42.
84х + 121(870-х) = 80850;
84х + 105270-121х = 80850;
84х -121х = 80850 -105270;
-37х = -24420;
х = 660.
Итак, на х или 660 тысяч рублей долг будет уменьшаться ежегодно в первые 5 лет.
За 2031 год выплата составит х + 0,1(4350-3х) = 0,7х+435. Так как х=660, то получим
0,7 ∙ 660 + 435 = 462 + 435 = 897 (тыс. рублей)
Ответ: 897 тысяч рублей.
На одной полке стоит 36 блюдец: 14 синих и 22 красных
Задача. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Решение. Будем брать 1 блюдце с первой полки и 1 чашку со второй полки, затем снова 1 блюдце с первой полки и 1 чашку со второй полки. Необходимо получить 2 чайные (одного цвета) пары. Подойдут следующие случаи:
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
Рассмотрим вероятность наступления каждого из этих случаев.
1)блюдце и чашка, блюдце и чашка — берём синее блюдце с первой полки (любое из 14, а всего 36 блюдец) и синюю чашку со второй полки (любую из 27, а всего 36 чашек), затем берём синее блюдце с первой полки (любое из 13, а всего 35 блюдец) и синюю чашку со второй полки (любую из 26, а всего 35 чашек). Эти 4 события независимы друг от друга, поэтому, вероятность их одновременного наступления равна произведению вероятностей выбора каждого из предметов:
Ответ: 0,29.
Задача. На одной полке стоит 25 блюдец: 16 красных и 9 синих. На другой полке стоит 25 чашек: 13 красных и 12 синих. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Решение. Будем брать 1 блюдце с первой полки и 1 чашку со второй полки, затем снова 1 блюдце с первой полки и 1 чашку со второй полки. Необходимо получить 2 чайные (одного цвета) пары. Подойдут следующие случаи:
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка.
Рассмотрим вероятность наступления каждого из этих случаев.
1) блюдце и чашка, блюдце и чашка – берём синее блюдце с первой полки (любое из 9, а всего 25 блюдец) и синюю чашку со второй полки (любую из 12, а всего 25 чашек), затем берём синее блюдце с первой полки (любое из 8, а всего 24 блюдец) и синюю чашку со второй полки (любую из 11, а всего 24 чашек). Эти 4 события независимы друг от друга, поэтому, вероятность их одновременного наступления равна произведению вероятностей выбора каждого из предметов:
Искомая вероятность p = p1 + p2 + p3 + p4 + p5 + p6.
Ответ: 0,38.
Делимость чисел. Теория сравнений. Малая теорема Ферма. Примеры
Если целые числа а и b при делении на натуральное число m дают равные остатки, то говорят, что эти числа сравнимы по модулю m, и пишут a ≡ b (mod m).
(знак ≡ читают: сравнимо)
Пример.
25 = 11 ∙ 2 + 3 (число 25 при делении на 11 даёт 3 в остатке).
69 = 11 ∙ 6 + 3 (число 69 при делении на 11 даёт 3 в остатке).
По определению выше числа 25 и 69 сравнимы по модулю 11, и, следовательно, справедлива запись: 25 ≡ 69 (mod 11).
У нас а = 25, b = 69, m = 11.
Запись a ≡ b (mod m) также означает, что число a-b делится на m.
Действительно, 25-69 = -44 делится на 11.
Так же верны записи: 25 ≡ 3 (mod 11) и 69 ≡ 3 (mod 11), так как число 3 при делении на 11 тоже даёт в остатке 3. Число 25 сравнимо с числом 3 по модулю 11. Число 69 сравнимо с числом 3 по модулю 11.
Числа 25-3 и 69-3 также делятся на 11 без остатка.
Поэтому запись a ≡ b (mod m) при b < m чаще трактуют так:
b – остаток при делении а на m.
25 ≡ 3 (mod 11) – остаток при делении 25 на 11 равен 3.
69 ≡ 3 (mod 11) – остаток при делении 69 на 11 равен 3.
Запись a ≡ 0 (mod m) означает, что число а делится на m без остатка.
Свойства сравнений.
Сравнения по одному модулю можно складывать, вычитать, перемножать и возводить в степень n (натуральное), как и верные числовые равенства. Покажем это на рассмотренных сравнениях
25 ≡ 3 (mod 11) и 69 ≡ 3 (mod 11).
Складываем. 25 + 69 ≡ 3 + 3 (mod 11) → 94 ≡ 6 (mod 11). При делении 94 на 11 в остатке получаем 6.
Вычитаем. 25-69 ≡ 3-3 (mod 11) → -44 ≡ 0 (mod 11). При делении -44 на 11 в остатке получаем 0, т.е. число -44 делится на 11 без остатка.
Перемножаем. 25 ∙ 69 ≡ 3 ∙ 3 (mod 11) → 1725 ≡ 9 (mod 11). При делении 1725 на 11 в остатке получаем 9.
Возводим в степень. Имеем 25 ≡ 3 (mod 11). А нам нужен остаток от деления 252 на 11.
25 ≡ 3 (mod 11) → 252 ≡ 32 (mod 11) → 625 ≡ 9 (mod 11).
Проверьте: при делении 625 на 11 в остатке получится 9.
Ещё одно свойство сравнений.
Если ak ≡ bk (mod m), m ≠ 1, а числа k и m взаимно просты, то a ≡ b (mod m). Обе части сравнения можно сокращать на общий множитель, если он и модуль m – взаимно простые числа.
А может остаток выражаться отрицательным числом? Да. Например, при делении числа 24 на 5 в остатке получается 4.
Значит, 24 ≡ 4 (mod 5), что означает: 24 — 4 делится на 5 без остатка.
Но запись 24 ≡ -1 (mod 5) так же верна, потому что 24 -(-1) = 25 также делится на 5 без остатка.
Записи 24 ≡ 4 (mod 5) и 24 ≡ -1 (mod 5) эквивалентны.
Ещё пример: 20 ≡ 6 (mod 7) и 20 ≡ -1 (mod 7) равнозначны,
так как 20-6 = 14 делится на 7, и 20-(-1) = 21 делится на 7 без остатка.
Малая теорема Фермá.
Если m — простое число, m и а – взаимно просты, то am-1–1 делится на m.
Следствие. Для простого m и любого натурального а число am — a делится без остатка на m.
Так как из утверждения am-1–1 делится на m следует, что am-1 ≡ 1 (mod m), то именно последнее утверждение удобно применять при нахождении остатков от деления степени числа а на простое число m при условии, что числа а и m взаимно просты. Понимаем так: число am-1 даёт в остатке 1 при делении на m.
Примеры.
Найти остаток от деления на 11 числа 22002 + 32002.
Решение.
Используем сравнение am-1 ≡ 1 (mod m). У нас m = 11, значит, m-1 = 10.
Выделим из степеней 22002 и 32002 степени 210 и 310.
22002 = 22 ∙ 22000 = 4 ∙ (210)200.
32002 = 32 ∙ 32000 = 9 ∙ (310)200.
22002 + 32002 = 4 ∙ (210)200 + 9 ∙ (310)200 ≡ 4 ∙ 1200 (mod 11) + 9 ∙ 1200 (mod 11) ≡ 4 + 9 (mod 11) ≡ 2 (mod 11). Искомый остаток равен 2.
Ответ: остаток от деления на 11 числа 22002 + 32002 равен 2.
Хотите подробнее?
Мы применили утверждение am-1 ≡ 1 (mod m).
На самом деле: 210 = 211-1 ≡ 1 (mod 11) и 310 = 311-1 ≡ 1 (mod 11), что на основании теоремы Фермá означает: числа 210 и 310 при делении на 11 дают в остатке 1.
Использовали свойство возведения в степень сравнений:
(210)200 ≡ 1200 (mod 11) ≡ 1 (mod 11), а затем свойство умножения и сложения сравнений:
4 ∙ 1 (mod 11) + 9 ∙ 1 (mod 11) ≡ 4 + 9 (mod 11) ≡ 13 (mod 11) ≡ 2 (mod 11), так как число 13 при делении на 11 даёт 2 в остатке.
А если нужно найти остаток от деления на 7 этого же числа?
Найти остаток от деления на 7 числа 22002 + 32002.
Решение. Рассуждаем точно так же.
Используем сравнение am-1 ≡ 1 (mod m). У нас m = 7, значит, m-1 = 6.
Выделим из степеней 22002 и 32002 степени 26 и 36.
22002 = 24∙ 21998 = 16 ∙ (26)333.
32002 = 34 ∙ 31998 = 81 ∙ (36)333.
22002 + 32002 = 16 ∙ (26)333 + 81 ∙ (36)333.
16 ≡ 2 (mod 7);
26 = 27-1 ≡ 1 (mod 7) → (26)333 ≡ 1333 (mod 7) ≡ 1 (mod 7);
81 ≡ 4 (mod 7);
36 = 37-1 ≡ 1 (mod 7) → (36)333 ≡ 1333 (mod 7) ≡ 1 (mod 7). Тогда получим:
22002 + 32002 = 16 ∙ (26)333 + 81 ∙ (36)333 ≡ 2 ∙ 1 + 4 ∙ 1 (mod 7) ≡ 6 (mod 7).
Ответ: остаток от деления на 7 числа 22002 + 32002 равен 6.
Найти остаток от деления на 11 числа 32002 + 72002 .
Решение.
На основании малой теоремы Фермá используем сравнение am-1 ≡ 1 (mod m).
У нас m = 11, значит, m-1 = 10.
Выделим из степеней 32002 и 72002 степени 210 и 310.
32002 = 32 ∙ 32000 = 9 ∙ (310)200.
72002 = 72 ∙ 22000 = 49 ∙ (210)200.
32002 + 72002 = 9 ∙ (210)200 + 49 ∙ (310)200 ≡ 9 ∙ 1200 + 49 ∙ 1200 (mod 11).
49 ≡ 5 (mod 11) т.к. при делении числа 49 на 11 в остатке будет 5. Получаем:
9 ∙ 1 + 5 ∙ 1 (mod 11) ≡ 14 (mod 11) ≡ 3 (mod 11) Искомый остаток равен 3.
Ответ: остаток от деления на 11 числа 32002 + 72002 равен 3.
Найти остаток от деления на 17 числа 2367 + 43.
Решение.
На основании малой теоремы Фермá ( а = 2, m = 17 – простое число, числа a и m – взаимно просты) используем сравнение am-1 ≡ 1 (mod m).
Так как m = 17, то m-1 = 16.
Выделим из степени 2367 степень 216.
2367 = 215 ∙ (216)22 = 210 ∙ 25 ∙ (216)22 = 1024 ∙ 32 ∙ (217-1)22.
1024 ≡ 4 (mod 17) – при делении 1024 на 17 получаем в остатке 4;
32 ≡ 15 (mod 17) – при делении 32 на 17 получаем в остатке 15;
217-1 ≡ 1 (mod 17).
Итак, 2367 = 1024 ∙ 32 ∙ (217-1)22 ≡ 4 ∙ 15 ∙ 1 (mod 17) ≡ 60 (mod 17) ≡ 9 (mod 17).
Тогда 2367 + 43 ≡ 9 + 43 (mod 17) ≡ 52 (mod 17) ≡ 1 (mod 17).
Ответ: остаток от деления на 17 числа 2367 + 43 равен 1.
Замечание. Мы могли бы вместо 32 ≡ 15 (mod 17) записать 32 ≡ -2 (mod 17).
И тогда 2367 = 1024 ∙ 32 ∙ (217-1)22 ≡ 4 ∙ (-2) ∙ 1 (mod 17) ≡ -8 (mod 17).
Отсюда 2367 + 43 ≡ -8 + 43 (mod 17) ≡ 35 (mod 17) ≡ 1 (mod 17).
Найти остаток от деления на 11 числа 32023.
Решение.
На основании малой теоремы Фермá имеем am-1 ≡ 1 (mod m).
Здесь а = 3, m = 11. Будет верным сравнение 311-1 ≡ 1 (mod 11).
32023 = 33 ∙ 32020 = 27 ∙ (310)202.
27 ≡ 5 (mod 11) – число 27 при делении на 11 даёт в остатке 5.
(310)202 = (311-1)202 ≡ 1202 (mod 11) ≡ 1 (mod 11).
Тогда 27 ∙ (310)202 ≡ 5 ∙ 1 (mod 11) ≡ 5 (mod 11).
Ответ: остаток от деления на 11 числа 32023 равен 5.
Найти остаток от деления на 11 числа 20212023.
Решение.
2021 ≡ 8 (mod 11), что означает: число 2021 сравнимо с числом 8 по модулю 11, так как при делении числа 2021 на число 11 в остатке получается 8.
20212023 ≡ 82023 (mod 11).
На основании малой теоремы Фермá имеем am-1 ≡ 1 (mod m).
Здесь а = 8, m = 11. Будет верным сравнение 811-1 ≡ 1 (mod 11).
82023 = 83 ∙ 82020 = 512 ∙ (810)202.
512 ≡ 6 (mod 11) и (810)202 = (811-1)202 ≡ 1202 (mod 11) ≡ 1 (mod 11).
Тогда 512 ∙ (810)202 ≡ 6 ∙ 1 (mod 11) ≡ 6 (mod 11).
Ответ: остаток от деления на 11 числа 20212023 равен 6.
Найти остаток от деления на 9 числа 23277.
Решение. число m = 9 (наш делитель) является составным, и теорема Ферма не применима.
Немного теории.
Если число А при делении на число m даёт в остатке d, то
An (mod m) ≡ dn ( mod m).
У нас 23 при делении на 9 даёт в остатке 5, поэтому
23277 (mod 9 ) ≡ 5277 (mod 9).
5277 (mod 9) ≡ 5 ∙ (53)92 (mod 9) ≡ 5 ∙ 12592 (mod 9) ≡ 5 ∙ 892 (mod 9) ≡
≡ 5 ∙ 6446 (mod 9) ≡ 5 ∙ 146 (mod 9) ≡ 5 (mod 9).
Ответ: остаток от деления на 9 числа 23277 равен 5.
Найти остаток от деления на 9 числа 102021 + 5.
Решение.
102021 ≡ 12021 (mod 9) ≡ 1 (mod 9). Ну на самом деле, ведь остаток от деления числа 10 на число 9 равен 1. И тогда:
102021 + 5 ≡ 1 + 5 (mod 9) ≡ 6 (mod 9).
Ответ: остаток от деления на 9 числа 102021 + 5 равен 6.
Найти остаток от деления на 5 числа 3946.
Решение.
Так как 39 = 5 ∙ 7 + 4, то 39 ≡ 4 (mod 5), следовательно, и
3946 ≡ 446 (mod 5).
446 = 42 ∙ 23 = (42)23 = 1623.
1623 ≡ 123 (mod 5) ≡ 1 (mod 5). При делении числа 16 на число 5 в остатке получается 1.
Ответ: остаток от деления на 5 числа 3946 равен 1.
Найти остаток от деления на 7 числа 6429.
Решение.
Так как 64 = 7 ∙ 9 +1, то 64 ≡ 1 (mod 7), следовательно, и
6429 ≡ 129 (mod 7) ≡ 1 (mod 7).
Ответ: остаток от деления на 7 числа 6429 равен 1.
Найти остаток от деления числа 3624 + 2145 + 78 на 10.
Решение.
Так как 36 ≡ 6 (mod 10), 21 ≡ 1 (mod 10), то данное число сравнимо с числом
624 + 145 + 78, и здесь нам не поможет малая теорема Фермá, так как не выполняются её основные условия: делитель должен быть простым числом, а основание степени и делитель взаимно просты. У нас же делитель m = 10, а это число составное.
Искомый остаток равен сумме остатков каждого из чисел 624, 145 и 78.
Любая степень числа 6 оканчивается цифрой 6, и при делении на 10 остаток будет равен 6.
Любая определённая степень числа 1 равна 1.
Подробнее рассмотрим степень числа 7.
71 = 7; 72 = 49; 73 = 343; 74 = 2401; 75 = 16807.
Мы поняли, что последние цифры таких чисел повторяются через 4.
Поэтому последняя цифра числа 7k, где k Є N, определяется только тем, каков остаток от деления числа k на 4. У нас 78 и k = 8, это число кратно 4, поэтому, последняя цифра числа 78 равна 1, как у числа 74.
Собираем остатки.
624 + 145 + 78 ≡ 6 + 1 + 1 (mod 10) ≡ 8 (mod 10).
Ответ: остаток от деления числа 3624 + 2145 + 78 на 10 равен 8.
Найти последнюю цифру числа 23275.
Решение. Задачу можно сформулировать иначе:
найти остаток от деления числа 23275 на 10.
Задача похожа на предыдущую.
23 ≡ 3 (mod 10). Это означает, что данное число будет иметь тот же остаток от деления на 10, что и число 3275.
Рассмотрим степени числа 3.
31 = 3; 32 = 9; 33 = 27; 34 = 81; 35 = 243, …
Последние цифры этих степеней повторяются через 4.
Поэтому последняя цифра числа 3k, где k Є N, определяется только тем, каков остаток от деления числа k на 4. У нас k = 275. Делим 275 на 4 и получаем в остатке 3. Значит, число 3275 оканчивается той же цифрой, что и число 33, т.е. цифрой 7.
Итак, 23275 ≡ 3275 (mod 10) ≡ 7 (mod 10).
Ответ: последняя цифра числа 23275 равна 7 или остаток от деления числа 23275 на число 10 равен 7.
Остаток от деления числа а на число 3 равен 1, а от деления на 7 равен 5. Чему равен остаток от деления числа а на 21?
Решение.
Запишем условие задачи на основании теории сравнений.
Известно: a ≡ 1 (mod 3) и a ≡ 5 (mod 7). Требуется найти х, если a ≡ x (mod 21).
Мы знаем, что если число делится на 21, то оно делится и на 3 и на 7, а это означает, что a ≡ x (mod 3), а также, что a ≡ x (mod 7).
Следовательно, х ≡ 1 (mod 3) и х ≡ 5 (mod 7).
Получается, что и число х при делении на 3 даёт в остатке 1, а при делении на 7 даёт в остатке 5. И это число меньше 21. Его несложно подобрать: х = 19.
На самом деле, 19 : 3 = 6 (ост 1); 19 : 7 = 2 (ост 5) или
19 ≡ 1 (mod 3) и 19 ≡ 5 (mod 7). Итак, a ≡ 19 (mod 21).
Ответ: 19.
Найти остаток от деления числа 59 ∙ 60 ∙ 61-62 на 7.
Решение. Воспользуемся свойствами умножения и сложения сравнений.
59 ∙ 60 ∙ 61–62 ≡ 59 (mod 7) ∙ 60 (mod 7) ∙ 61 (mod 7)–62 (mod 7) ≡
≡ 3 ∙ 4 ∙ 5–6 (mod 7) ≡ 54 (mod 7) ≡ 5 (mod 7).
Ответ: 5.
Найти остаток от деления на 7 числа 6543 + 5432.
Решение.
Так как 65 ≡ 2 (mod 7) и 54 ≡ 5 (mod 7), то задача сводится к нахождению остатка от деления числа 243 + 532 на число 7.
На основании малой теоремы Фермá используем сравнение am-1 ≡ 1 (mod m). У нас m = 7, значит, m-1 = 6.
Выделим из степеней 243 и 532 степени 26 и 56.
243 = 2∙ 242 = 2 ∙ (26)7.
532 = 52 ∙ 530 = 25 ∙ (56)5.
243 + 532 = 2 ∙ (26)7 + 25 ∙ (56)5.
25 ≡ 4 (mod 7);
26 = 27-1 ≡ 1 (mod 7) → (26)7 ≡ 17 (mod 7) ≡ 1 (mod 7);
56 = 57-1 ≡ 1 (mod 7) → (56)5 ≡ 15 (mod 7) ≡ 1 (mod 7). Тогда получим:
2 ∙ (26)7 + 25 ∙ (56)5 ≡ 2 ∙ 1 + 4 ∙ 1 (mod 7) ≡ 6 (mod 7).
Ответ: остаток от деления на 7 числа 6543 + 5432 равен 6.
Найти остаток от деления на 11 числа 229.
Решение.
На основании малой теоремы Фермá имеем am-1 ≡ 1 (mod m).
Здесь а = 2, m = 11. Будет верным сравнение 211-1 ≡ 1 (mod 11).
229 = 29 ∙ 220 = 512 ∙ (210)2.
512 ≡ 6 (mod 11) – число 512 при делении на 11 даёт в остатке 6.
(210)2 = (211-1)2 ≡ 12 (mod 11) ≡ 1 (mod 11).
Тогда 512 ∙ (210)2 ≡ 6 ∙ 1 (mod 11) ≡ 6 (mod 11).
Ответ: остаток от деления на 11 числа 229 равен 6.
Найти остаток от деления числа 3217 + 3522 на 10.
Решение.
Так как 32 ≡ 2 (mod 10), 35 ≡ 5 (mod 10), то данное число сравнимо с числом
217 + 522, и здесь нам не поможет малая теорема Фермá, так как не выполняются её основные условия: делитель должен быть простым числом, а основание степени и делитель взаимно просты. У нас же делитель m = 10, а это число составное.
Искомый остаток равен сумме остатков каждого из чисел 217 и 522.
Любая степень числа 5 оканчивается цифрой 5, и при делении на 10 остаток будет равен 5.
Подробнее рассмотрим степень числа 2.
21 = 2; 22 = 4; 23 = 8; 24 = 16; 25 = 32.
Мы поняли, что последние цифры таких чисел повторяются через 4.
Поэтому последняя цифра числа 2k, где k Є N, определяется только тем, каков остаток от деления числа k на 4. У нас 217 = 24∙4+1, следовательно, последняя цифра числа 217 равна 2, как у числа 21. Итак:
217 + 522 ≡ 2 + 5 (mod 10) ≡ 7 (mod 10).
Ответ: остаток от деления числа 3217 + 3522 на 10 равен 7.
Найти остаток от деления числа 2013 ∙ 2014 + 20152 на число 7.
Решение.
Используем свойства сравнений.
Найдём остатки от деления чисел 2013, 2014 и 2015 на 7.
2013 ≡ 4 (mod 7); 2014 ≡ 5 (mod 7); 2015 ≡ 6 (mod 7).
2013 ∙ 2014 + 20152 ≡ 4 ∙ 5 + 62 (mod 7) ≡ 56 (mod 7) ≡ 0 (mod 7).
Это означает, что данное число делится нацело на 7.
Ответ: остаток от деления числа 2013 ∙ 2014 + 20152 на число 7 равен 0.
Найти остаток от деления числа 2016 + 2016 на 9.
Решение.
По теории сравнений 20 ≡ 2 (mod 9) и 201 ≡ 3 (mod 9).
На основании свойств сравнений:
2016 + 2016 ≡ 216 + 36 (mod 9), и нам нужно найти остаток от деления числа
216 + 36 на 9. Заметим, что число 36 делится на 9 нацело, и остаток равен 0.
Найдём остаток от деления на 9 числа 216. Это и будет ответом к данной задаче.
216 = (26)2 ∙ 24 = 642 ∙ 16 ≡ 12 ∙ 7 (mod 9) ≡ 7 (mod 9).
Ответ: остаток от деления числа 2016 + 2016 на 9 равен 7.
Хотите порешать такие примеры самостоятельно? Отлично! Лучше решать их в виде теста онлайн — вы сразу будете видеть свои результаты и отзывы к вашим решениям. Тест «Делимость чисел» многовариантный, так что пока решаете 2-3 варианта — научитесь!
15 декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 16 месяцев
15 декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 16 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг будет возрастать на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 15-го месяца долг должен быть равен 500 тысяч рублей;
— к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что сумма всех платежей после полного погашения кредита будет составлять 1228 тысяч рублей.
Решение.
За 15 месяцев банку заплатили 1100 — 500 = 600 тысяч рублей основного долга,
И, следовательно, 600 : 15 = 40 тысяч рублей – это та сумма, на которую ежемесячно уменьшается долг.
Однако, r % ежемесячно нужно выплачивать с суммы остатка долга, начиная с выданной суммы кредита 1100 тысяч рублей, а затем с суммы за вычетом 40 тысяч рублей ежемесячно. Проценты считаются так:
1 месяц. 1100 ∙ 0,01r = 11r;
2 месяц (1100 — 40) ∙ 0,01r = 1060 ∙ 0,01r = 10,6r;
3 месяц (1060 — 40) ∙ 0,01r =1020 ∙ 0,01r = 10,2r;
4 месяц (1020 — 40) ∙ 0,01r = 980 ∙ 0,01r = 9,8r и так далее.
Заметим, что последовательность чисел 11r; 10,6r; 10,2r; 9,8r и т.д. представляет собой арифметическую прогрессию с первым членом
а1 = 11r и разностью d = -0,4r. Нам нужно найти сумму 15-ти членов этой арифметической прогрессии. Воспользуемся формулой:
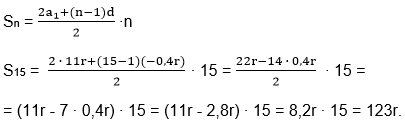
Итак, банку придётся отдать 600 тысяч рублей плюс 123r тысяч рублей процентов за первые 15 месяцев и ещё за 16-й месяц долг 500 тысяч рублей плюс проценты с этой суммы, т.е. r % от 500 тысяч (это 0,01r ∙ 500 = 5r). Общая сумма выплат по условию равна 1228 тысяч рублей. Получим равенство:
600+123r+500+5r = 1228;
128r = 128;
r = 1.
Ответ: 1%.
А можно рассуждать так.
Решение2.
За 15 месяцев банку заплатили 1100 — 500 = 600 тысяч рублей основного долга,
И, следовательно, 600 : 15 = 40 тысяч рублей – это та сумма, на которую ежемесячно уменьшается долг в первые 15 месяцев.
Однако, r % ежемесячно нужно выплачивать с суммы остатка долга, начиная с выданной суммы кредита 1100 тысяч рублей, а затем с суммы за вычетом 40 тысяч рублей ежемесячно. Проценты считаются так:
1 месяц. 1100 ∙ 0,01r;
2 месяц (1100 — 40) ∙ 0,01r = 1060 ∙ 0,01r;
3 месяц (1100 — 40 ∙ 2) ∙ 0,01r =1020 ∙ 0,01r;
4 месяц (1100 — 40 ∙ 3) ∙ 0,01r = 980 ∙ 0,01r;
……………………………………………………..
15 месяц (1100 — 40 ∙ 14) ∙ 0,01r = 540 ∙ 0,01r.
Сложим полученные результаты, вынеся общий множитель 0,01r за скобки:
(1100+1060+1020+980+…+540) ∙ 0,01r. Это сумма процентов за 15 месяцев.
В скобках сумма 15-ти членов арифметической прогрессии с первым членом
а1 = 1100 и пятнадцатым членом а15 = 540.
Тогда 12300 ∙ 0,01r = 123r тысяч рублей составят начисленные банком проценты за первые 15 месяцев.
За последний 16-й месяц, когда долг останется равным 500 тысяч рублей, банк возьмёт r % с этой суммы, т.е. 500 ∙ 0,01r = 5r тысяч рублей.
Следовательно, начисленные банком за всё время кредитования проценты составят
123r +5r =128r тысяч рублей.
По условию сумма всех платежей после полного погашения кредита (1100 тысяч рублей) будет составлять 1228 тысяч рублей. Это означает, что на проценты банку приходится 1228-1100=128 тысяч рублей.
Имеем равенство 128r = 128, отсюда r = 1%.
Ответ: 1%.
Ну всё понятно! А как же оформить эту задачу на ЕГЭ?
Решение.
Банку будет выплачена сумма взятого кредита 1100 тысяч рублей плюс проценты. Так как по условию вся выплаченная сумма 1228 тысяч рублей, то сумма процентов составит 128 тысяч рублей. В первые 15 месяцев будет выплачено 1100-500=600 тысяч рублей основного долга, следовательно, долг ежемесячно уменьшается на 600:15=40 тысяч рублей.
Проценты (r % ежемесячно) начисляются на остаток долга так, как показано в таблице.
15 числа 15-го месяца будут выплачены последний раз 40 тысяч рублей, и долг станет равным 500 тысяч рублей. На эту сумму также будет начислено r %, т.е.
500 ∙ 0,01r = 5r тысяч рублей.
Всего переплата 123r + 5r = 128r или 128 тысяч рублей. Отсюда r = 1%.
Ответ: 1%.
Напоминание. Чтобы найти проценты от числа, нужно обратить проценты в десятичную дробь, а затем умножить данное число на эту дробь.
Примеры.
45% от числа 1100 равны 0,45 ∙ 1100 = 495;
3% от 1100 равны 0,03 ∙ 1100 = 33;
r% от 1100 равны 0,01r ∙ 1100 = 11r.
Производная. Часть 1
Определение понятия производной и её геометрического смысла
показано на рисунке 1, а подробно раскрыто в видео, которое можно посмотреть на
YouTube: https://youtu.be/OniFjwZ3b00
RUTUBE: https://rutube.ru/video/0fd4e77d6cd661ed4d2cbc1c96137f10/
ЯндексДзен: https://zen.yandex.ru/video/watch/623be27502c2cc69a1db251a
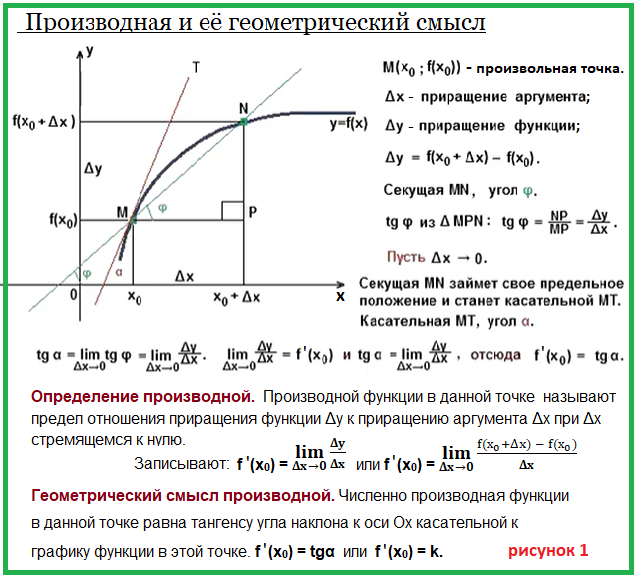
Поясним новые понятия.
Приращение аргумента Δх и приращение функции Δу.
Во-первых, для функции y = f(x)
х –аргумент; у – функция.
Приращение аргумента Δх — это величина, на которую изменяют (увеличивают, как на рисунке, или уменьшают) абсциссу х0 произвольной точки М графика, причём значение Δх незначительно отличается от зафиксированного значения х0.
В результате получается новое значение аргумента х = х0 + Δх. Этому новому значению аргумента соответствует новая точка графика N,
у которой координаты (x0+Δx; f(x0+Δx)). Что же получилось? Мы увеличили абсциссу точки М на Δх и в результате ордината увеличилась на Δу = f(x0+Δx) -f(x0).
Что такое lim.
В переводе limit – предел, предельное значение при определённом условии.
Что означает знак ( ′ ) штрих. Это знак производной.
f(x) – функция; f ′(x) – производная функции.
производная функции f в точке х0 равна пределу отношения приращения функции Δу к приращению аргумента Δх при Δх стремящемся к нулю.
В чём заключается геометрический смысл производной?
Производная функции в данной точке есть угловой коэффициент
прямой у = kx + b (на рисунке прямая МТ), которая служит касательной
к графику функции y = f(x) в точке с абсциссой х0.
А так как коэффициент k = tgα, где α – угол между касательной и положительным направлением оси Ох, то имеем равенство:
f ′(x0) = k = tgα. В этом и состоит геометрический смысл производной.
Используя равенство f ′(x0) = tgα, вы легко решите такие задания ЕГЭ,
как задача 6 ЕГЭ 2022 ФИПИ.
Примеры.
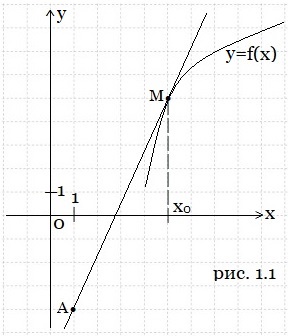
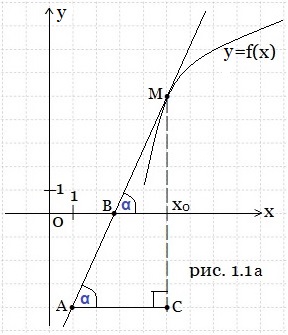
Пример 1. На рисунке 1.1 изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Решение. М – точка касания (рис. 1.1а). Касательная МА пересекает ось Ох в точке В и образует угол МВХ с положительным направлением оси Ох. Обозначим этот угол через α. Искомое значение производной функции f(x) в точке х0 равно тангенсу угла α. Построим прямоугольный треугольник АСМ с гипотенузой МА. Угол МАС также равен α. Найдём тангенс угла α из ΔАСМ. Считаем клеточки (единичные отрезки). МС = 9, АС = 4.
Так как f ′(x0) = tgα, то получаем f ′(x0) = 2,25.
Ответ: 2,25.
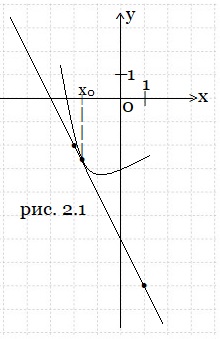
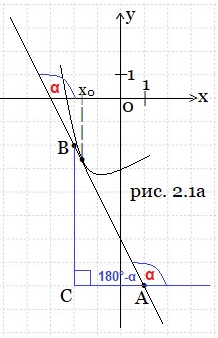
Пример 2. На рисунке 2.1 изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Решение. Касательная АВ (рис. 2.1а) к графику функции y = f(x) в точке х0 образует угол α с положительным направлением оси Ох.
Искомое значение f ′(x0) = tgα. Вначале из прямоугольного треугольника АВС найдём тангенс угла ВАС, смежного с углом α. У нас ВС = 6, АС = 3.
Нас интересует tgα.
Так как tg(180°-α) = -tgα, то tgα = -tg(180°-α) = -2.
Тогда f ‘(x0) = tgα = -2. Ответ: -2.
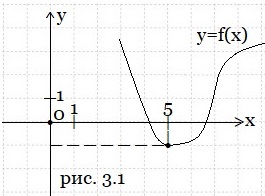
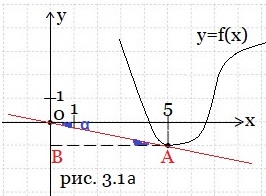
Пример 3. На рисунке 3.1 изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите значение производной функции f(x) в точке х0 = 5.
Решение. Касательная АО (рис. 3.1а) образует тупой угол с положительным направлением оси Ох. Найдём тангенс острого угла α смежного с этим тупым углом, а значения тангенсов смежных углов отличаются лишь знаком.
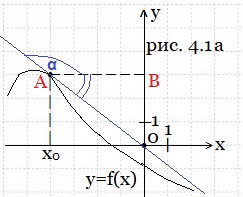
Пример 4. На рисунке 4.1 изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой -4. Найдите значение производной функции f(x) в точке х0 = -4.
Решение. Касательная АО (рис. 4.1а) образует тупой угол α с положительным направлением оси Ох. Найдём тангенс смежного с углом α угла ОАВ из прямоугольного треугольника АВО.
По свойству смежных углов ∠ОАВ=180°-α.
Мы найдём тангенс угла (180°-α) и воспользуемся равенством
tgα = -tg(180°-α).
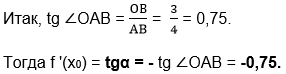
Ответ: -0,75.
Формулы и правила производной
Возникает вопрос. А как находить производную функции, если нет никаких рисунков?
Ответ. По формулам, выведенным согласно определения производной, т.е. на основании равенства:
Потребуется только равенство y = f(x), где f(x) – выражение, содержащее переменную х.
В качестве примера рассмотрим вывод формулы производной степени.
На основании определения производной получим формулу:
(хn)′ = nxn-1.
Смотрите рисунок 2. Подробности на видео.
YouTube: https://youtu.be/gNqs6svP61A
RUTUBE: https://rutube.ru/video/c2722daedf644bdf1da071fb8656a9b0/
ЯндексДзен: https://zen.yandex.ru/video/watch/623fd665de9aa25e6dd7247c
Итак, мы имеем формулу ( хn )′ = nxn-1.
Примеры. Найти производные следующих функций.
1) у =х6. Решение. у′ = 6х5.
2) у = х. Решение. у′ = 1х0 = 1.
х′ = 1.
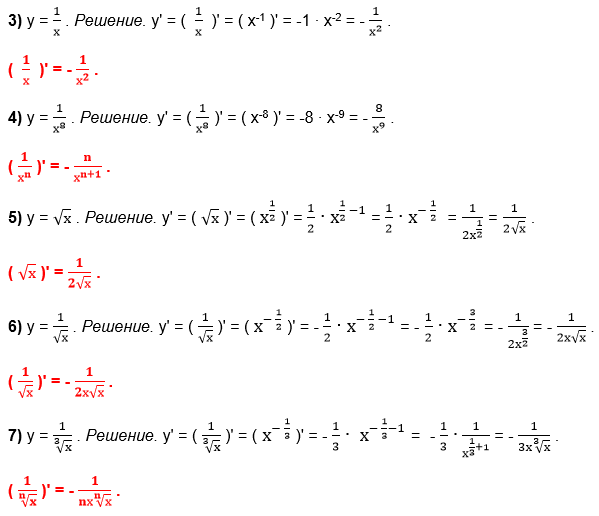
На основании определения производной выводятся и производные других элементарных функций.
Операцию нахождения производной функции называют дифференцированием этой функции.
Вопрос. Многие функции представляют собой сумму, разность, произведение или частное некоторых функций f(x) и g(x). Как быть в этих случаях?
Ответ. Применяют правила дифференцирования, которые выводятся также на основании определения производной функции. Для удобства введём обозначения: u = f(x) и v = g(x).
1. Производная суммы (разности) равна сумме (разности) производных.
(u ± v)′ = u ′ ± v ′
2. Производная произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
(uv)′ = u′v + uv′
3. Постоянный множитель можно вынести за знак производной.
(Сu)′ = Cu′.
4. Производная постоянной величины равна нулю.
С ′ = 0.
5. Производная дроби равна дроби, числитель которой есть произведение производной числителя исходной дроби на знаменатель минус произведение числителя исходной дроби на производную знаменателя, а знаменатель результата равен квадрату знаменателя исходной дроби.
Сложная функция
Вопрос. Что такое сложная функция? Как найти производную сложной функции?
Ответ. Функцию от функции называют сложной функцией.
Пример 1. Функция у = (2х + 3)7 является сложной, так как это степенная функция от линейной функции.
Это функция арифметического квадратного корня от квадратичной функции.
В общем виде: функция у = f(u(x)) сложная. Функция f зависит от функции u,
а функция u зависит от х, так что х – аргумент сложной функции.
6. Производную сложной функции f(u(x)) находят по переменной х. Для этого вначале находят производную функции f по переменной u и результат умножают на производную функции u по переменной х.
Применим эту формулу к функции у = (2х + 3)7 (пример 1).
Здесь f(u) = u7; u(x) = 2x+3.
Тогда у ‘ = 7u6 ∙ (ux)′ = 7(2х + 3)6 ∙ (2х + 3)’ = 7(2х + 3)6 ∙ 2 = 14(2х + 3)6.
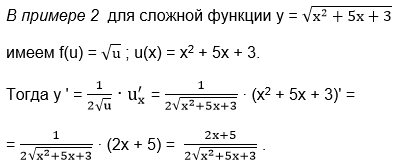
Уравнение касательной
Уравнение касательной к графику функции y=f(x) в точке с абсциссой х0 имеет вид:
y = f(x0) + f ‘(x0)(x —x0). Смотрите рисунок 3.
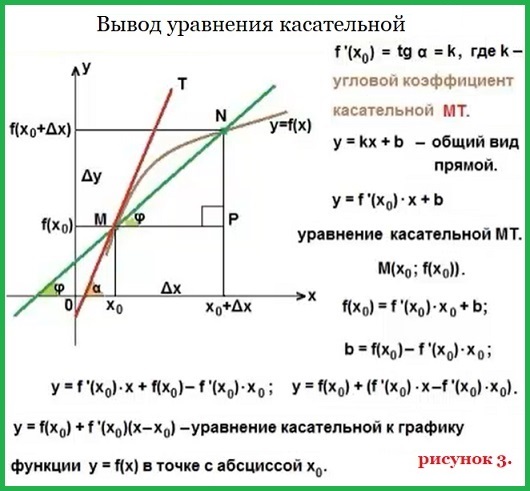
Смотрите видео вывода уравнения касательной.
YouTube: https://youtu.be/F2FGE0njy2U
RUTUBE: https://rutube.ru/video/8ce780b3a7c20e73db21515620c1089f/
ЯндексДзен: https://zen.yandex.ru/video/watch/623d2a7cd1c13971d8c16e66
Пример 1. Написать уравнение касательной к графику функции
у = х3 + 3х в точке с абсциссой х0 = 3.
Решение. Искомое уравнение касательной имеет вид:
y = f(x0) + f ′(x0)(x -x0).
Требуется найти f(x0) и f ‘(x0), а затем подставить найденные значения в уравнение касательной.
f(x0) = f(3) = 33 + 3∙3 = 27 + 9 = 36.
f ′(x) = (х3 + 3х)′ = 3х2 + 3.
f ′(x0) = f ′(3) = 3∙32 + 3 = 30.
Получаем у = 36 + 30(х -3); у = 36 + 30х -90;
у = 30х -54 – искомое уравнение касательной.
Пример 2. Написать уравнение касательной к графику функции
у = -2х2-12х-13 в точке с абсциссой х0 = -4. Сделать рисунок.
Решение. Искомое уравнение касательной имеет вид:
y = f(x0) + f ‘(x0)(x-x0).
Требуется найти f(x0) и f ‘(x0), а затем подставить найденные значения в уравнение касательной.
f(x0) = f(-4) = -2∙(-4)2-12∙(-4)-13 = -32+48-13 = 3.
f ‘(x) = (-2х2-12х-13)’ = -4x-12.
f ‘(x0) = f ‘(-4) = -4∙(-4)-12 = 16-12 = 4.
Получаем у = 3 + 4(х + 4); у = 3 + 4х + 16;
у = 4х + 19 – искомое уравнение касательной.
Сделаем рисунок.
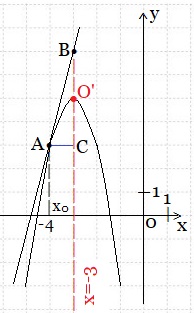Графиком функции у = -2х2-12х-13 служит парабола с вершиной О’(m; n).
n = y(m) = y(-3) = -2∙(-3)2-12∙(-3)-13 = -18+36-13 = 5.
О’(-3; 5) – вершина параболы. Ветви параболы направлены вниз, так как отрицателен коэффициент
а = -2 при х2.
От точки (-3; 5) как от начала координат строим параболу у = -х2 (или построим одну-две дополнительные точки и используем свойство симметрии параболы относительно своей оси х = m).
Наша касательная у = 4х +19 касается параболы в точке А(-4; 3). Это одна точка прямой. Если взять х = -3, то получим у = 4∙(-3) + 19 = 7. Это точка В(-3; 7).
Проведём прямую (нашу касательную) через точки А и В.
Задание выполнено. Мы потрудились, а теперь полюбуемся своей работой и вспомним, в чём заключается геометрический смысл производной. Через точку А проведём прямую, параллельную оси Ох до точки пересечения с осью параболы (х = -3), которую обозначим через С. Угол ВАС – это угол между касательной к параболе в точке х0 и положительным направлением оси Ох. Из прямоугольного треугольника АСВ тангенс угла ВАС равен отношению противолежащего катета ВС к прилежащему катету АС и равен 4:1 = 4.
В самом деле, могло ли быть иначе? Так как уравнение нашей касательной
у = 4х + 19, то угловой коэффициент k = tg∠ВАС = 4. И это найденное нами ранее значение f ‘(x0).
Итак, мы убедились на примере:
f ‘(x0) = k = tgα = 4.
Производная функции в данной точке есть угловой коэффициент
прямой у = 4x + 19 (на рисунке прямая АВ), которая служит касательной
к графику функции y = -2х2-12х-13 в точке с абсциссой х0 = -4. В этом суть геометрического смысла производной.
Механический (физический) смысл производной
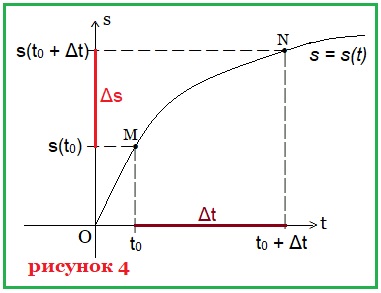Рассмотрим движение материальной точки по некоторой траектории (рисунок 4).
На горизонтальной оси Оt мы будем отмечать время пути, а на вертикальной оси Os — расстояние, пройденное точкой за определённое время.
Зафиксируем точку М в момент времени t0.
Пройденный точкой путь на момент времени t0 равен s(t0) — значению функции в точке М.
Если в момент времени t координата материальной точки равна s, где s = s(t), то функцию s(t) называют законом движения материальной точки.
За промежуток времени Δt наша материальная точка совершила перемещение из положения М в положение N. Таким образом в момент времени t = t0 + Δt точкой пройден путь s(t0 + Δt), и, следовательно, за время Δt точка преодолела путь
Δs = s(t0 + Δt) — s(t0).
Среднюю скорость движения точки от М до N определим по формуле
Средняя скорость тем полнее характеризует движение, чем короче участки пути, на которых она определена. Поэтому один из возможных способов описания неравномерного движения состоит в задании средних скоростей этого движения на всё более и более малых участках пути. Логично, что малые участки пути будут соответствовать малым промежуткам времени.
Пусть Δt стремится к нулю. Это означает, что от времени t0 до времени t = t0 + Δt прошло буквально мгновение, и точка N практически неотличима от точки М.
А что же произойдёт со скоростью ?
Предел этой скорости при Δt → 0 называется мгновенной скоростью движения в момент времени t:
Знакомо? Да это же определение производной!
Предел отношения приращения пути Δs к приращению времени Δt при Δt стремящимся к нулю есть производная пути s по времени t.
А в результате получилась скорость v(t).
Говорят, что скорость есть производная пути по времени: v(t) = s‘(t).
Аналогично можно показать, что
ускорение есть производная скорости по времени: a(t) = v‘(t).
В последних двух формулировках и заключается механический (физический) смысл производной.
Пример 1. (Задача 6 ЕГЭ) Материальная точка движется прямолинейно по закону
x(t) = t3 + 4t2 -3t + 15, где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 7 с.
Решение.
Так как скорость есть производная пути по времени,
то в нашем случае v(t) = х’ (t) = (t3 + 4t2 -3t + 15)’.
v(t) = 3t2 + 8t-3.
Тогда скорость в момент времени t = 7 найдём, подставив это значение 7 в последнее равенство.
v(7) = 3 ∙ 72 + 8 ∙ 7-3 = 3 ∙ 49 + 56-3 = 200. Ответ: 200.
Пример 2. (Задача 6 ЕГЭ) Материальная точка движется прямолинейно по закону
x(t) = t2 -9t -22, где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) её скорость была равна 3 м/с?
Решение. Скорость есть производная пути по времени, поэтому
v(t) = х’ (t) = (t2 -9t -22)’.
v(t) = 2t -9.
Найдём время t, зная скорость v = 3 в момент этого времени.
3 = 2t -9 → 2t = 12 → t = 6. Ответ: 6.
Пример 3. Точка движется прямолинейно по закону x(t) = 2t3 + t -1.
В какой момент времени ускорение будет равно 6 см/с2?
(x(t) – перемещение в сантиметрах, t – время в секундах.)
Решение. Скорость есть производная пути по времени, поэтому
v(t) = х’ (t) = (2t3 + t -1)’ = 6t2 + 1.
Ускорение есть производная скорости по времени: a(t) = v‘(t).
У нас a(t) = (6t2 + 1)’ = 12t.
Итак, a(t) = 12t. Найдём момент времени t при котором по условию ускорение
a(t) = 6.
6 = 12t → t = 6 : 12 → t = 0,5. Ответ: 0,5.
Решить логарифмическое неравенство
Решите неравенство lg4(x2 – 26)4 – 4lg2(x2 – 26)2 ≤ 240.
Применим формулу для логарифма степени и запишем
lg(x2 – 26)4 как 2lg(x2 – 26)2. А почему не как 4lg(x2 – 26)? Потому что в этом случае число под знаком логарифма должно быть положительным, а не просто не равным нулю, как мы записали в ОДЗ. Это значит, что преобразованное далее неравенство не будет равносильно данному. Итак:
lg4(x2 – 26)4 = (lg(x2 – 26)4 )4 = (2lg(x2 – 26)2 )4 = 24 · (lg(x2 – 26)2 )4 = 16lg4(x2 – 26)2.
Тогда данное неравенство примет вид:
16lg4(x2 – 26)2 – 4lg2(x2 – 26)2 ≤ 240. Делим обе части на 4.
4lg4(x2 – 26)2 – lg2(x2 – 26)2 – 60 ≤ 0.
Сделаем замену. Пусть lg2(x2 – 26)2 = t.
Решим неравенство. 4t2 – t – 60 ≤ 0.
Находим корни квадратного трёхчлена.
4t2 – t – 60 = 0. D = b2 – 4ac = 1 + 960 = 961 = 312.
0 ≤ lg2(x2 – 26)2 ≤ 4.
lg2(x2 – 26)2 ≤ 4. Извлекаем из обеих частей квадратные корни.
| lg(x2 – 26)2| ≤ 2.
-2 ≤ lg(x2 – 26)2 ≤ 2. (см. рис. 2)
Запишем числа -2 и 2 в виде десятичного логарифма.
lg0,01 ≤ lg(x2 – 26)2 ≤ lg100. Логарифмическая функция с основанием 10 является возрастающей, поэтому последнее неравенство равносильно неравенству
0,01 ≤ (x2 – 26)2 ≤ 100. А это неравенство равносильно системе неравенств
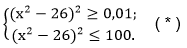
Решаем каждое неравенство системы по отдельности, а затем находим их общее решение. Оно и будет служить решением данного неравенства.
I. (x2 – 26)2 ≥ 0,01; (см. рис.3)
| x2 – 26| ≥ 0,1;
1) x2 – 26 ≤ -0,1
x2 ≤ 25,9.
2) x2 – 26 ≥ 0,1
x2 ≥ 26,1.
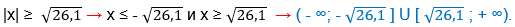
Решаем второе неравенство системы ( * )
II. (x2 – 26)2 ≤ 100;
| x2 – 26| ≤ 10;
-10 ≤ x2 – 26 ≤ 10
16 ≤ x2 ≤ 36;
Полученные решения неравенств I и II покажем синим и зелёным цветом на координатной прямой. Пересечение этих промежутков и будет решением нашего неравенства.
Тригонометрические уравнения на ЕГЭ
Пример 1.
а) Решить уравнение cos4x+cos2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-π; π/3].
Решение.
а) Решаем уравнение cos4x+cos2x=0.
Применим формулу 
Tогда данное уравнение примет вид: 2cos3x⋅cosx=0. Отсюда следует, что либо cos3x=0 либо cosx=0.
- Если cos3x=0, то 3х=π/2+πn, отсюда х=π/6+πn/3, где nϵZ.
- Если cosx=0, то х=π/2+πn, где nϵZ.
Заметим, что решения уравнения cosx=0 входят в решения уравнения cos3x=0, поэтому общим решением данного уравнения будут числа x=π/6+πn/3, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [-π; π/3].
Рассмотрим общее решение x=π/6+πn/3, где nϵZ на единичной окружности. Здесь значение πn/3 означает, что нужно брать n раз угол π/3. Отмечаем угол π/6, а затем углы, полученные поворотом угла π/6 на π/3, полученный таким образом угол π/2 опять повернём на π/3, получится угол 5π/6, затем угол 5π/6+ π/3=7π/6, следующий угол
7π/6+ π/3=9π/6=3π/2, и, наконец, 3π/2+ π/3=11π/6. Смотрите рисунок 1.
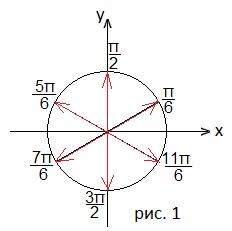
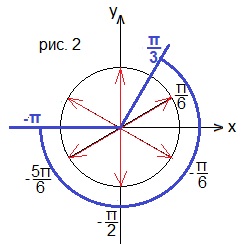
Все отмеченные углы рассмотрим на отрезке [-π; π/3]. Смотрим рисунок 2. Получились числа -5π/6; -π/2; -π/6; π/6.
Ответ: а) π/6+πn/3, где nϵZ; б) -5π/6; -π/2; -π/6; π/6.
Пример 2.
а) Решить уравнение cos4x-sin2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [0; π].
Решение.
а) Применим формулу 1-cos2α=2sin2α; тогда данное уравнение примет вид:
1-2sin22x-sin2x=0; 2sin22x+sin2x-1=0. Сделаем замену: sin2x=t.
Получаем равенство: 2t2+t-1=0.
У нас a-b+c=0, поэтому по методу коэффициентов t1=-1, t2=1/2.
- При sin2x=-1 получаем 2х=-π/2+2πn, отсюда х=-π/4+πn, где nϵZ.
- При sin2x=1/2 получаем 2х=π/6+2πn и 2х=5π/6+2πn, где nϵZ.
Тогда х=π/12+πn и х=5π/12+πn, где nϵZ.
Рассмотрим решения 2х=-π/2+2πn, 2х=π/6+2πn и 2х=5π/6+2πn на единичной окружности. Возьмём значения 2х при n=0. Углы -π/2, π/6 и 5π/6 отличаются друг от друга на значение 2π/3. Тогда общим решением будут являться числа
2х=π/6+(2π/3)n, отсюда общим решением данного уравнения будут
значения х=π/12+(π/3)n, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [0; π]. Для этого в общее решение х=π/12+(π/3)n, где nϵZ будем подставлять такие целые значения nϵZ,
чтобы хϵ[0; π].
Возьмём n=0, тогда х=π/12 ϵ[0; π].
При n=1 получим х= π/12+π/3= π/12+4π/12=5π/12 ϵ[0; π].
При n=2 получим х= π/12+2π/3= π/12+8π/12=9π/12=3π/4 ϵ[0; π].
При n=3 получим х= π/12+π, и это значение не входит в заданный отрезок [0; π].
Ответ: а) π/12+(π/3)n, где nϵZ; б) π/12, 5π/12, 3π/4.
Пример 3.
а) Решить уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Решение.
а) Применим формулу cos(α-β)=cosα∙cosβ+sinα∙sinβ; тогда данное уравнение примет вид:
cos3x=cos23x; cos23x-cos3x=0; cos3x(cos3x-1)=0;
cos3x=0 или cos3x-1=0.
- Если cos3x=0, то 3х=π/2+πn, тогда х= π/6+(π/3)n, где nϵZ.
- Если cos3x-1=0, то cos3x=1, тогда 3х=2πm, тогда х=(2π/3)m, где mϵZ.
Общие решения данного уравнения: х=π/6+(π/3)n, где nϵZ и х=(2π/3)m, где mϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Мы получили значения 3х=π/2+πn и 3х=2πm. Отметим их на единичной окружности, сделав замену 3х=t. Смотрите рисунок 3.
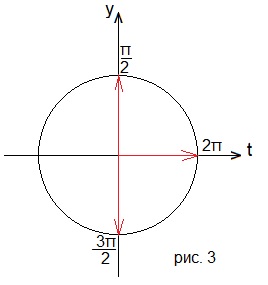
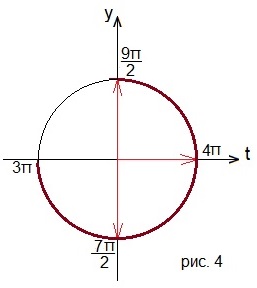
Необходимо выполнение условие хϵ[π; 3π/2]. Отсюда следует, что 3хϵ[3π; 9π/2].
Все отмеченные углы рассмотрим на отрезке [3π; 9π/2]. Смотрим рисунок 4. Получились числа 7π/2; 4π; 9π/2. Так как это значения 3х, то делим каждое из них на 3. Получим: 7π/6; 4π/3; 3π/2.
Ответ: а) π/6+(π/3)n, где nϵZ; (2π/3)m, где mϵZ.
б) 7π/6; 4π/3; 3π/2.
