Найдите все такие значения а, при каждом из которых
ЕГЭ 2022 ФИПИ Вариант 5. Задача 17
Задача. Найдите все такие значения а, при каждом из которых неравенство
-1 ≤ sinx(a-cos2x) ≤ 1 верно при всех действительных значениях х.
Решение. Видео решение этой задачи.
Применим формулу 1-cos2x = 2sin2x.
-1 ≤ sinx(a+2sin2x-1) ≤ 1. Сделаем замену. Пусть sinx = t.
Так как |sinx| ≤ 1 при любом х ∈ (- ∞; +∞),
то t ∈ [-1; 1]. Получаем:
-1 ≤ t(a+2t2 -1) ≤ 1.
Примечательно, что если мы разделим все части последнего двойного неравенства на любое (отрицательное или положительное) значение
t ≠ 0, то получится неравенство:
![]()
Прибавим ко всем частям неравенства выражение -2t2 +1.
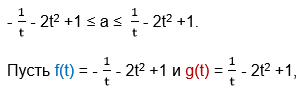
причём, области определения этих функций D(f) = D(g) = [-1; 0) U (0; 1].
Тогда f(t) ≤ а ≤ g(t).
Получается, что число а больше или равно наибольшему значению функции f(t), и в это же время а меньше или равно наименьшему значению функции g(t), т.е.
max f(t) ≤ а ≤ min g(t).
Итак, нам необходимо найти максимум функции f(t) и минимум функции g(t).
Воспользуемся понятием производной.

Найдём промежутки убывания и возрастания функции f(t).
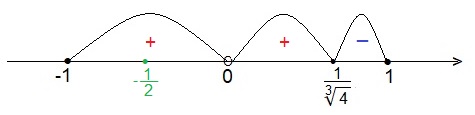

функция f(t) меняет знак с «+» на «-», следовательно, это точка максимума функции. Находим значение максимума функции f(t).
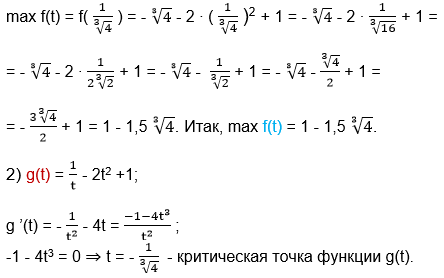
Найдём промежутки убывания и возрастания функции g(t).
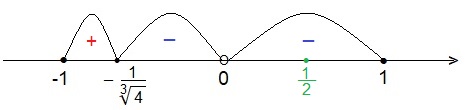

точек минимума не имеет. Это означает, что наименьшее значение функция будет иметь в точке t = 1.
Тогда min g(t) = g(1) = 1 -2 + 1 = 0.
Итак, min g(t) = 0.
Так как max f(t) ≤ а ≤ min g(t),
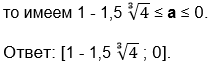
ЕГЭ 2022 ФИПИ Вариант 6. Задача 17
Задача. Найдите все такие значения а, при каждом из которых неравенство
-1 ≤ cosx(cos2x-a-1) ≤ 1 верно при всех действительных значениях х.
Решение.
Применим формулу 1+cos2x = 2cos2x.
-1 ≤ cosx(2cos2x-1-a-1) ≤ 1
-1 ≤ cosx(2cos2x-a-2) ≤ 1. Сделаем замену. Пусть cosx = t.
Так как |cosx| ≤ 1 при любом х ∈ (- ∞; +∞),
то t ∈ [-1; 1]. Получим:
-1 ≤ t(2t2 -a -2) ≤ 1.
Если мы разделим все части последнего двойного неравенства на любое (отрицательное или положительное) значение t ≠ 0, то получится неравенство:

Области определения этих функций D(f) = D(g) = [-1; 0) U (0; 1].
Тогда f(t) ≤ а ≤ g(t).
Получается, что число а больше или равно наибольшему значению функции f(t), и в это же время а меньше или равно наименьшему значению функции g(t), т.е.
max f(t) ≤ а ≤ min g(t).
Итак, нам необходимо найти максимум функции f(t) и минимум функции g(t).
Сделаем это с помощью производной.

Найдём промежутки убывания и возрастания функции f(t).
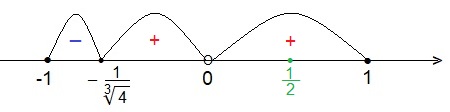
Итак, функция f(t) возрастает при

не имеет точек максимума, поэтому, наибольшее своё значение функция будет иметь в точке t = 1. Находим значение максимума функции f(t).
max f(t) = f(1) = 2-1-2 = -1.
Итак, max f(t) = -1.
Рассмотрим функцию g(t).
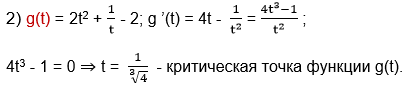
Найдём промежутки убывания и возрастания функции g(t).
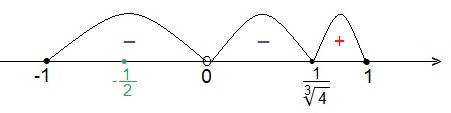




Комментирование закрыто.