Задания на векторы в 1 части профильного ЕГЭ по математике

Задача. Даны векторы \( \vec{a}\ \)(2; 3) и  \( \vec{b}\ \)(-3; b₀). Найдите b₀, если |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите меньшее из них.

Решение.

Модуль вектора \( \vec{a}\ \)(а₁; а₂) равен квадратному корню из суммы квадратов его координат:

\( | \vec{a}|=\sqrt{(a_1)^2+(a_2)^2}\ \);

\( | \vec{a}|=\sqrt{2^2+3^2}\ \); \( | \vec{a}|=\sqrt{13}\ \).

Найдём модуль вектора \( \vec{b}\ \)(-3; b₀).

\( | \vec{b}|=\sqrt{(-3)^2+(b_0)^2}\ \);

\( | \vec{b}|=\sqrt{9+(b_0)^2}\ \).

По условию |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.

Получаем b² = 2,25a².

9 + (b₀)² = 2,25 ∙ 13;

9 + (b₀)² = 29,25;

(b₀)² = 20,25;

b₀ = ±4,5.

В ответе требуется записать меньшее из значений b₀.

Ответ: -4,5.

Задача. Даны векторы \( \vec{a}\ \)(4; -1) и  \( \vec{b}\ \)(b₀; 8). Найдите b₀, если |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите большее из них.

Решение.

Найдём модуль вектора \( \vec{a}\ \)(4; -1).

\( | \vec{a}|=\sqrt{4^2+(-1)^2}\ \);

\( | \vec{a}|=\sqrt{17}\ \).

Найдём модуль вектора \( \vec{b}\ \)(b₀; 8).

\( | \vec{b}|=\sqrt{(b_0)^2+8^2}\ \);

\( | \vec{b}|=\sqrt{(b_0)^2+64}\ \);

По условию |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.

Получаем b² = 6,25a².

(b₀)² + 64 = 6,25 ∙ 17;

(b₀)² + 64 = 106,25;

(b₀)² = 42,25;

b₀ = ±6,5.

В ответе требуется записать большее из значений b₀.

Ответ: 6,5.

Задача. Даны векторы \( \vec{a}(-1; 3)\ \), \( \vec{b}(4; 1)\ \), \( \vec{c}(2; c_0)\ \). Найдите с₀, если \( ( \vec{a}+\vec{b})\: \cdot \: \vec{c} =0\ \).  

Решение.

Скалярное произведение векторов равно сумме произведение соответственных координат этих векторов.

3 ∙ 2 + 4 ∙ с₀ = 0;

с₀ = -6 : 4;

с₀ = -1,5.

Ответ: -1,5.

Задача. Даны векторы \( \vec{a}(3; -1)\ \), \( \vec{b}(2; 0)\ \), \( \vec{c}(4; c_0)\ \). Найдите с₀, если \( ( \vec{a}- \vec{b})\: \cdot \: \vec{c} =0\ \). 

Решение аналогично решению предыдущей задачи.

1 ∙ 4 + (-1) ∙ с₀ = 0;

-с₀ = -4;

с₀ = 4.

Ответ: 4.

Задача. Даны векторы \( \vec{a}(-2; 4)\ \)и \( \vec{b}(2; -1)\ \). Известно, что векторы \( \vec{c}(x_c; y_c)\ \)и  \( \vec{b}\ \) сонаправленные, а \( | \vec{c}|=| \vec{a}|\ \). Найдите х_с+у_с.

Решение.

Так как длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и  \( \vec{b}\ \) сонаправлены, то и координаты вектора \( \vec{c}(x_c; y_c)\ \) больше координат вектора \( \vec{b}\ \) в два раза.

Получаем х_с = 2 ∙ 2 = 4 и у_с = -1 ∙ 2 = -2.

Тогда х_с + у_с = 4 + (-2) = 2.

Ответ: 2.

Задача. Даны векторы \( \vec{a}(4; -6)\ \)и \( \vec{b}(-2; 3)\ \). Известно, что \( | \vec{c}|=| \vec{a}|\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) противоположно направленные. Найдите х_с+у_с.  

Решение аналогично решению предыдущей задачи.

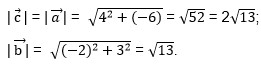
Длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и  \( \vec{b}\ \), по условию, противоположно направлены, следовательно отношение координат вектора \( \vec{c}(x_c; y_c)\ \) к соответственным координатам вектора \( \vec{b}\ \) равно (-2).

Получаем х_с = -2 ∙ (-2) = 4 и у_с = -2 ∙ 3 = -6.

Тогда х_с + у_с = 4 + (-6) = -2.

Ответ: -2.

Каждую из двух предыдущих задач можно решить быстро и легко графическим способом.

Смотрите видео.

Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}\ \), если \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). В ответ запишите сумму координат вектора \( \vec{c}\ \).

Решение.

Определим координаты данных векторов.

       

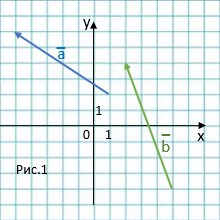
Каждая координата вектора равна разности соответствующих координат его конца и начала.

Смотрим рис. 2.

А₁(1; 2) и А₂(-5; 6); В₁(5; -4) и В₂(2; 4). Тогда

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

По условию \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). Следовательно,

Таким образом, сумма координат вектора \( \vec{c}\ \) равна 4,5.

Ответ: 4,5.

Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}(x_c; y_c)\ \), если \( \vec{c}=\vec{a}-1,5 \vec{b}\ \).

В ответ запишите произведение х_с ∙ у_с.

Решение аналогично решению предыдущей задачи.

   

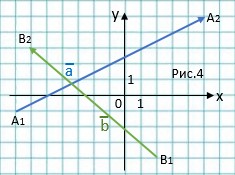
Определим координаты данных векторов.

Смотрим рис. 4.

А₁(-7; -1) и А₂(5; 5); В₁(2; -4) и В₂(-6; 3). Тогда

По условию \( \vec{c}=\vec{a}-1,5 \vec{b}\ \). Следовательно,

Таким образом, искомое произведение координат вектора \( \vec{c}\ \)

х_с ∙ у_с = 24 ∙ (- 4,5) = -108.

Ответ: -108.

Задача. Даны векторы \( \vec{a}(4; y_a)\ \)и \( \vec{b}(x_b; 0)\ \), косинус угла между которыми равен \( \frac{2}{\sqrt{5}}\ \). Найдите у_а. Если таких значений несколько, в ответ запишите большее из них.  

Решение.

Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла φ между ними.

В прямоугольной системе координат скалярное произведение векторов

\( \vec{a}(x_1; y_1)\ \)и \( \vec{b}(x_2; y_2)\ \) выражается формулой

\( \vec{a} \cdot \vec{b} =x_1x_2+y_1y_2\ \)

Получаем равенство:

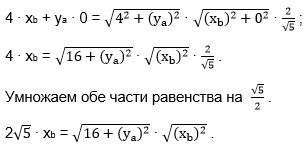
Возведём обе части равенства в квадрат:

20 ∙ (x_b)² = (16 + (y_a)²) ∙ (x_b)²; делим на (x_b)² обе части равенства:

20 = 16 + (у_а)²;

(у_а)² = 4;

у_а = ±2.

Большее из этих значений у_а = 2.

Ответ: 2.

Задача. Даны векторы \( \vec{a}(x_a; -2)\ \)и \( \vec{b}(0; y_b)\ \), косинус угла между которыми равен \( -\sqrt{0,2}\ \). Найдите x_а. Если таких значений несколько, в ответ запишите меньшее из них. 

Решение аналогично решению предыдущей задачи.

Составим равенство на основании формулы:

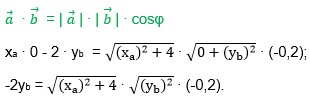
Разделим обе части равенства на (-0,2).

Возведём обе части равенства в квадрат:

20 ∙ (у_b)² = ((х_a)² + 4) ∙ (у_b)²; делим на (у_b)² обе части равенства:

20 = (х_а)² + 4;

(х_а)² = 16;

х_а = ±4.

Меньшее из этих значений х_а = -4.

Ответ: -4.

Задача. Даны векторы \( \vec{a}(14; -2)\ \)и \( \vec{b}(-7; -1)\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \). 

Решение.

Найдём модули данных векторов.

Получаем:

14 ∙ (-7) + (-2) ∙ (-1) = 10 ∙ 5 ∙ cosα;

-98 + 2 = 100 ∙ cosα, отсюда cosα = -0,96.

Ответ: -0,96.

Задача. Даны векторы \( \vec{a}(-6; 2)\ \)и \( \vec{b}(9; 13)\ \). Найдите косинус угла между

векторами \( \vec{a}\ \)и \( \vec{b}\ \). 

Решение аналогично решению предыдущей задачи.

Находим модули данных векторов.

Получаем:

-6 ∙ 9 + 2 ∙ 13 = 2 ∙ 5 ∙ cosα;

-54 + 26 = 100 ∙ cosα;

-54 + 26 = 100 ∙ cosα;

-28 = 100 ∙ cosα;

отсюда cosα = -0,28.

Ответ: -0,28.