Найдите все значения а, при каждом из которых система уравнений имеет более двух решений

Задача. Найдите все значения а, при каждом из которых система уравнений имеет более двух решений

Решение. Так как правая часть равенства неотрицательна, то неотрицательной будет и левая часть неравенства.

Следовательно, x²-8x + y² + 4y + 15 ≥ 0.

Выделим из алгебраических сумм (x²-8x) и (y² + 4y) полные квадраты двучленов.

x²-2 ∙ х ∙ 4 + 4²-4² + y² + 2 ∙ y ∙ 2 + 2²-2² + 15 ≥ 0;

(x²-2 ∙ х ∙ 4 + 4²) + (y² + 2 ∙ y ∙ 2 + 2²) + 15 ≥ 16 + 4-15;

(х-4)² + (у + 2)² ≥ 5.

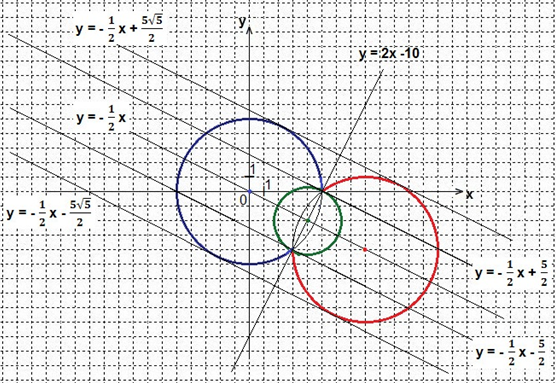
ОДЗ: решения системы находятся среди множества точек, лежащих вне окружности с центром в точке Q(4; -2) и радиусом R =√5 . Смотрите рисунок. Эта окружность изображена зелёным цветом

1) Раскроем модульные скобки в первом уравнении системы, считая подмодульное выражение отрицательным,

т.е. при 2х-у-10 < 0.

Запишем это неравенство в виде: у > 2x -10. Получаем:

x²-8x + y² + 4y + 15 = 4 ∙ (-2х + у + 10);

x²-8x + y² + 4y + 15 = -8х + 4у + 40;

x² + y² = 25. Графически это уравнение изображает окружность с центром в начале координат и радиусом R = 5.

Решением первого уравнения при условии у > 2x -10 является множество точек

окружности x² + y² = 25, лежащих выше прямой у = 2x-10 и находящихся вне окружности (х-4)² + (у + 2)² = 5. Эти точки изображены синим цветом.

2) Раскроем модульные скобки в первом уравнении системы, считая подмодульное выражение неотрицательным, т.е. при 2х-у-10 ≥ 0.

Запишем это неравенство в виде: у ≤ 2x -10. Получаем:

x²-8x + y² + 4y + 15 = 4 ∙ (2х-у-10);

x²-8x + y² + 4y + 15 = 8х-4у-40;

x²-16х + y² + 8у = -55. Преобразуем это уравнение к виду:

x²-2 ∙ х ∙ 8 + 8²-8² + y² + 2 ∙ y ∙ 4 + 4²-4² = -55;

(x²-2 ∙ х ∙ 8 + 8²)-8² + (y² + 2 ∙ y ∙ 4 + 4²)-4² = -55 + 64 + 16;

(х-8)² + (у + 4)² = 25.

Графически это уравнение изображает окружность с центром

в точке (8; -4) и радиусом R = 5. Нам подойдут те точки этой окружности, которые лежат ниже прямой у = 2х-10  и находящиеся вне окружности  (х-4)² + (у + 2)² = 5. Изображаем эти точки красным цветом.

3) Второе уравнение данной системы уравнений х + 2у = а запишем в виде:

занимала промежуточное положение между касательными к зелёной окружности и касательными к синей и красной окружностям, при этом последние касательные не подойдут, так как только в двух точках будут пересекать окружности. Числовое значение параметра а мы найдём, решив системы уравнений:

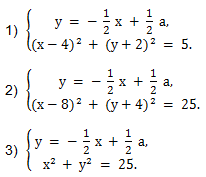
Будем решать каждую систему уравнений методом подстановки: значение у из первого уравнения подставляем во второе уравнение и получаем квадратное уравнение относительно переменной х. Далее потребуем, чтобы дискриминант квадратного уравнения был равен нулю. В этом случае квадратное уравнение, а значит и каждая система (1-3) будет иметь единственное решение, зависящее от значения а,

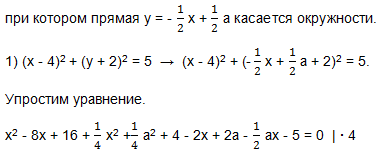
4x²-32x + 64 + x² + a² + 16-8x + 8a-2ax-20 = 0;

5x²-40x-2ax + 60 + a² + 8a = 0;

5x²-2(20 + a)x + a² + 8a + 60 = 0. Находим дискриминант по формуле для чётного второго коэффициента.

D₁ = (20 + a)²-5(a² + 8a + 60) = 400 + 40a + a²-5a²-40a-300 = 100-4a².

D₁ = 0   →   100-4a²   →   a² = 25   →  a = ±5.

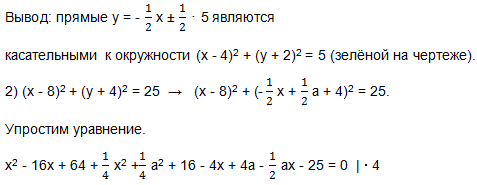
х²-16х + 64 +  х² + а² + 16-4х + 4а-ах-25 = 0  | ∙ 4

4x²-64x + 256 + x² + a² + 64-16x + 16a-2ax-100 = 0;

5x²-80x-2ax + a² + 16a + 220 = 0;

5x²-2(40 + a)x + a² + 16a + 220 = 0. Находим дискриминант по формуле для чётного второго коэффициента.

D₁ = (40 + a)²-5(a² + 16a + 220) = 1600 + 80a + a²-5a²-80a-1100 = 500-4a².

D₁ = 0   →   500-4a²   →   a² = 125 .

являются касательными к окружности (х-8)² + (у + 4)² = 25 (красной на чертеже).

3) Убедимся, что к окружности x² + y² = 25 (синей окружности) касательными

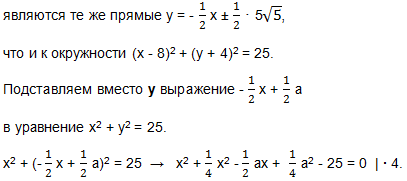
4х² + х²-2ах + а²-100 = 0   →   5х²-2ах + а²-100 = 0.

Дискриминант D₁ = a²-5(a²-100) = a²-5a² + 500 = 500-4a². Смотрим рассуждения в пункте 2) и убеждаемся в том, что и к синей окружности касательными являются прямые