На рисунке изображены графики функций f(x) и g(x)
Задача. На рисунке изображены графики функций
f(x) = ax2 + bx + c и g(x) = kx + d, которые пересекаются в точках А и В.
Найдите абсциссу точки В.
Решение. Смотреть видео.
1) Парабола. Очевидно, что записать уравнение данной квадратичной функции в виде y = a(x-m)2 + n не получится, т.к координаты вершины параболы (точка (m, n)) не выражается целыми числами. Будем искать уравнение квадратичной функции в виде f(x) = ax2 + bx + c. Значение с – это ордината точки пересечения параболы с осью Оу. Обозначим эту точку буквой С(0; -4). Так что имеем:
 у = ax2 + bx -4. Парабола проходит через точку А(-2; -2), поэтому верно равенство:
у = ax2 + bx -4. Парабола проходит через точку А(-2; -2), поэтому верно равенство:
-2 = a ∙ (-2)2 + b ∙ (-2) -4. Упростим и получим 2а- b = 1. Также парабола проходит через точку D(1; 1). Тогда верным будет равенство:
1 = а + b -4. Упростим и получим а + b = 5. Сложим полученные равенства
2а- b = 1 и а + b = 5
и получим 3а = 6, отсюда а = 2.
Подставим значение а = 2 в равенство а + b = 5 и получим b = 3.
Уравнение параболы имеет вид у = 2х2 + 3х -4.
2) Прямая. Наша прямая проходит через точки А(-2; -2) и Е(-1; 2).
Используем общую формулу уравнения прямой, проходящей через
точки (х1; у1) и (х2; у2):
![]()
У нас х1 = -2, у1 = -2; х2 = -1, у2 = 2. Подставляем эти значения в последнее равенство.

у + 2 = 4(х + 2);
у = 4х + 6 – уравнение прямой АЕ.
3) для того, чтобы найти точки пересечения прямой и параболы, решим систему полученных уравнений:

Решаем первое уравнение системы.
2х2 + 3х -4 = 4х + 6; 2х2-х -10 = 0.
Дискриминант D = 81, x1 = -2; x2 = 2,5.
![]()
Графики пересекаются в точках А(-2; -2) и В(2,5; 16).
Нас интересует только абсцисса точки В. Ответ: 2,5.
ЕГЭ 2022 ФИПИ Вариант 6. Задача 9
Задача. На рисунке изображены графики функций
f(x) = 3х + 3 и g(x) = ax2 + bx + c, которые пересекаются в точках
А(-1; 0) и В(х0; у0). Найдите у0.
Решение. Смотреть видео.
1) Парабола. Запишем уравнение данной квадратичной функции в виде
y = a(x-m)2 + n, где m и n – координаты вершины параболы.
 У нас m = -2 и n = 1.
У нас m = -2 и n = 1.
Тогда g(x) = а(х + 2)2 + 1. Если значение а неочевидно, то используем то, что парабола проходит через точку С(-4; -3), поэтому, подставив её координаты в равенство
g(x) = а(х + 2)2 + 1, получим верное равенство:
-3 = a ∙ (-4+2)2 + 1. Упростим и получим
-4 = 4а, отсюда а = -1.
Уравнение параболы имеет вид
g(x) = -(х + 2)2 + 1 или
у = -х2 -4х -3.
2) для того, чтобы найти точки пересечения прямой и параболы, решим систему уравнений:

Решаем первое уравнение системы.
-х2 -4х- 3 = 3х + 3; после преобразований:
х2 +7х + 6 = 0. По теореме Виета x1 = -6; x2 = -1.
![]()
Графики пересекаются в точках А(-1; 0) и В(-6; -15).
Нас интересует только ордината точки В. Ответ: -15.
Графики функций на клетчатой бумаге
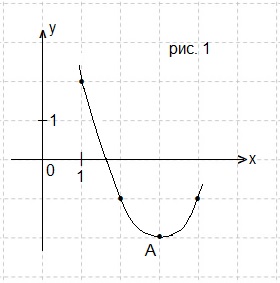
Задача 1. На рисунке 1 изображён график функции
f(x) = ax2 + bx + c, где числа a, b и c — целые. Найдите f(-8).
Решение.
 Квадратичную функцию f(x) = ax2 + bx + c также можно представить в виде:
Квадратичную функцию f(x) = ax2 + bx + c также можно представить в виде:
f(x) = a(x-m)2 + n, где m и n — координаты вершины параболы, а – коэффициент сжатия.
На рисунке мы видим параболу. Мысленно перенесём её вершину в начало координат и понимаем, что в этом случае на рисунке окажется график привычной нам функции
у = х2, т.е. а = 1.
У нашей параболы вершина находится в точке A(3; -2), т.е. m = 3, n = -2.
Получаем y = (x-3)2-2. Это и есть функция, график которой изображён на рисунке 1. Нам нужно найти f(-8), поэтому нет необходимости преобразовывать полученную функцию к виду f(x) = ax2 + bx + c.
Мы просто подставим число -8 вместо х.
f(-8) = y(-8) = (-8-3)2-2 = 121-2 = 119.
Ответ: 119.
Задача 2. На рисунке 2 изображён график функции
f(x) = ax2 + bx + c, где числа a, b и c — целые. Найдите f(7).
Решение.
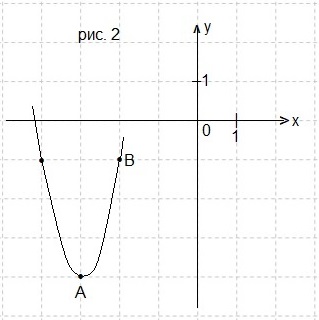 Вершина параболы А(-3; -4),
Вершина параболы А(-3; -4),
Искомую функцию запишем в виде:
y = a(x-m)2 + n, где m и n – координаты вершины параболы.
У нас m = -3, n = -4.
Получаем у = а(х+3)2-4.
Подставляем в это равенство координаты точки В(-2; -1) и найдём коэффициент а.
-1 = а(-2+3)2-4;
-1 = а-4, значит, а = 3.
Итак, уравнение параболы, изображённой на рисунке: у = 3(х+3)2-4.
А теперь находим значение f(7).
у(7) = 3(7+3)2-4 = 3 ∙ 100-4 = 296. Ответ: 296.
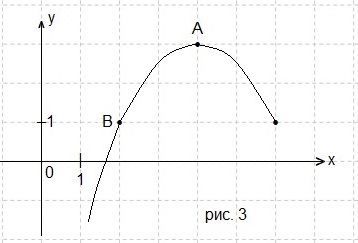
Задача 3. На рисунке 3 изображён график функции
f(x) = ax2 + bx + c, где числа a, b и c — целые. Найдите f(-5).
Решение.
 Рассуждаем точно так же!
Рассуждаем точно так же!
Вершина параболы А(4; 3),
Квадратичную функцию запишем в виде y = a(x-m)2 + n, где m и n – координаты вершины параболы.
У нас m = 4, n = 3.
Получаем у = а(х-4)2 + 3.
Для того, чтобы найти коэффициент а, в полученное уравнение подставим координаты точки В(2; 1).
1 = а(2-4)2 + 3;
1 = 4а + 3;
4а = -2, отсюда а = -0,5.
у = -0,5(х 4)2 + 3 – уравнение функции, график которой изображён на рисунке.
А теперь находим значение f(-5).
у(-5) = -0,5 ∙ (-5-4)2 + 3 = -0,5 ∙ 81 + 3 = -40,4 + 3 = -37,5. Ответ: -37,5.
Однако, могут быть случаи, когда на рисунке не представляется возможным указать точные значения координат вершины параболы. Как быть? Рассмотрим пример.
Задача 4. На рисунке 4 изображён график функции
f(x) = ax2 + bx + c, где числа a, b и c — целые. Найдите f(-10).
Решение.
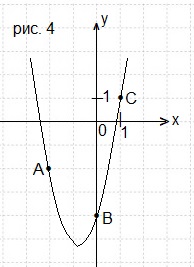 График функции у = ax2 + bx + c пересекает ось Ох в точке В(0; -4), следовательно, значение с = -4.
График функции у = ax2 + bx + c пересекает ось Ох в точке В(0; -4), следовательно, значение с = -4.
Теперь функция имеет вид: у = ax2 + bx-4.
Осталось найти значения а и b.
Так как парабола проходит через точки
А(-2; -2) и В(1; 1), то, подставив координаты этих точек в равенство у = ax2 + bx-4, мы получим систему уравнений:
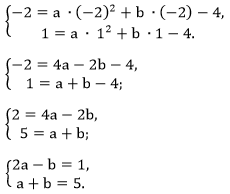
Почленно сложим равенства и получим 3а = 6, отсюда а = 2.
Подставим это значение в равенство a + b = 5, тогда b = 3.
Получаем функцию f(x = 2x2 + 3x-4. Находим f(-10).
у(-10) = 2 ∙ (-10)2 + 3 ∙ (-10)-4 = 200-30-4 = 166. Ответ: 166.
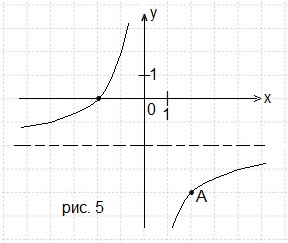
Задача 5. На рисунке 5 изображён график функции f(x) =k/x + a. Найдите f(-10).
Решение.
Немного теории.
 На рисунке мы видим гиперболу, состоящую из двух ветвей. Это график дробно-линейной функции вида:
На рисунке мы видим гиперболу, состоящую из двух ветвей. Это график дробно-линейной функции вида:
![]()
Правую часть равенства легко можно преобразовать к виду:
![]()
где x = m – вертикальная асимптота графика,
y = n – горизонтальная асимптота графика.
Асимптота – прямая, к которой неограниченно приближается график функции, но которую никогда не пересечёт.
Смотрим на рисунок.
Вертикальная асимптота х = 0 (ось Оу), следовательно, m = 0.
Горизонтальная асимптота у = -2 (штрих-пунктирная прямая),
следовательно, n = -2. Тогда наша функция принимает вид:
![]()
Для нахождения коэффициента k в полученное равенство подставим координаты точки А(2; -4).
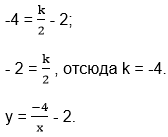
Это уравнение функции, график которой изображён на рисунке.
Отвечаем на вопрос задачи.
![]()
Ответ: -1,6.
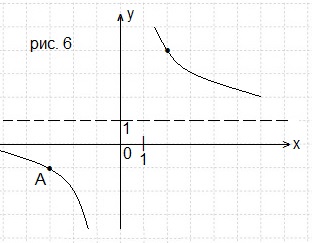
Задача 6. На рисунке 6 изображён график функции f(x) =k/x + a. Найдите f(24).
Решение.
 Запишем функцию в виде:
Запишем функцию в виде:
![]()
где x = m – вертикальная асимптота графика,
y = n – горизонтальная асимптота графика.
Вертикальная асимптота х = 0 (ось Оу), следовательно, m = 0.
Горизонтальная асимптота у = 1 (штрих-пунктирная прямая),
следовательно, n = 1. Тогда наша функция принимает вид:
![]()
Для нахождения коэффициента k в полученное равенство подставим координаты точки А(-3; -1).
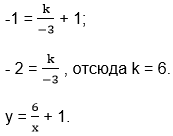
Это уравнение функции, график которой изображён на рисунке.
Отвечаем на вопрос задачи.
![]()
Ответ: 1,25.
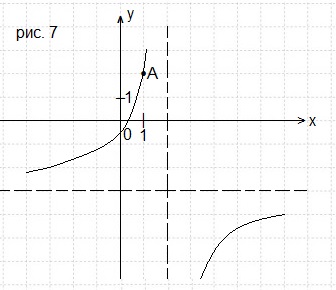
Задача 7. На рисунке 7 изображён график функции f(x) = (kx+a)/(x+b).
Найдите значения k и а.
Решение.
 Будем искать функцию в виде:
Будем искать функцию в виде:
![]()
где x = m – вертикальная асимптота графика,
y = n – горизонтальная асимптота графика.
Вертикальная асимптота х = 2 (вертикальная штрих-пунктирная прямая),
следовательно, m = 2.
Горизонтальная асимптота у = -3 (горизонтальная штрих-пунктирная прямая),
следовательно, n = -3. Тогда наша функция принимает вид:
![]()
Подставим в это уравнение вместо х и у координаты точки А(1; 2).

Осторожно! Это не искомое k.

Ответ: k = -3; a = 1.
Как составить уравнение прямой по её графику?
Задача 8. Записать уравнения прямых AB, CD, EF и PK, изображённых на рисунке.
Пусть прямые AB и EF пересекаются в точке М(х0; у0). Найти абсциссу точки пересечения.
Решение.
Рассмотрим различные способы составления уравнения прямой по её изображению.
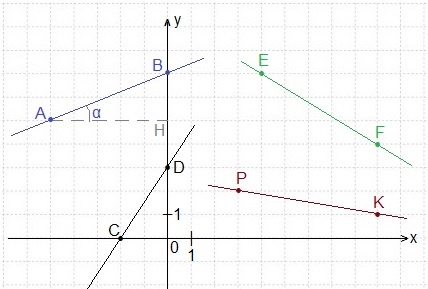
1) Прямая АВ является графиком линейной функции y = kx + b.
Значение b – это ордината точки В(0; 7) — пересечения прямой АВ с осью Оу.
У нас b = 7.
![]()
Тогда уравнение прямой АВ: у = 0,4х + 7.
2) Прямая CD пересекла ось Ох в точке С(-2; 0), а ось Оу — в точке D(0; 3). Так как прямая CD отсекает отрезки от координатных осей, то можно использовать уравнение прямой в отрезках:

у = 1,5х+3. Это уравнение прямой CD.
3) Прямая EF проходит через точки E(x1; y1) и F(x2; y2). Уравнение прямой будем искать в виде y = kx + b. Значение k найдём по формуле:
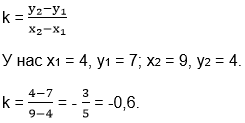
Теперь уравнение прямой EF имеет вид у = -0,6х + b.
Для нахождения значения b подставим координаты точки Е(4; 7) в последнее равенство:
7 = -0,6 ∙ 4 + b, отсюда b = 7 + 2,4 = 9,4.
Окончательно, EF: у = -0,6х + 9,4.
4) Уравнение прямой РК запишем в виде ax + by = c, используя уравнение прямой, проходящей через точки (х1; у1) и (х2; у2):
![]()
У нас Р(3; 2) и К(9; 1), т.е. х1 = 3, у1 = 2; х2 = 9, у2 = 1. Подставляем эти значения в последнее равенство.
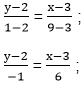
6(у-2) = -(х-3);
6у-12 = -х + 3;
х + 6у = 15 – уравнение прямой РК.
5) По условию прямые AB и EF пересекаются в точке М(х0; у0). Требуется найти абсциссу точки пересечения, т.е. нужно найти значение х0.
Уравнение прямой АВ: у = 0,4х + 7.
Уравнение прямой EF: у = -0,6х + 9,4.
Решаем совместно эти уравнения. Левые части этих уравнений равны, следовательно, равны и правые части:
0,4х + 7 = -0,6х + 9,4;
0,4х + 0,6х = 9,4-7;
х = 2,4. Это искомая абсцисса х0 точки М, в которой пересекаются прямые AB и EF.


