Задания на векторы в 1 части профильного ЕГЭ по математике
Задача. Даны векторы \( \vec{a}\ \)(2; 3) и \( \vec{b}\ \)(-3; b0). Найдите b0, если |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите меньшее из них.
Решение.
Модуль вектора \( \vec{a}\ \)(а1; а2) равен квадратному корню из суммы квадратов его координат:
\( | \vec{a}|=\sqrt{(a_1)^2+(a_2)^2}\ \);
\( | \vec{a}|=\sqrt{2^2+3^2}\ \); \( | \vec{a}|=\sqrt{13}\ \).
Найдём модуль вектора \( \vec{b}\ \)(-3; b0).
\( | \vec{b}|=\sqrt{(-3)^2+(b_0)^2}\ \);
\( | \vec{b}|=\sqrt{9+(b_0)^2}\ \).
По условию |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.
Получаем b2 = 2,25a2.
9 + (b0)2 = 2,25 ∙ 13;
9 + (b0)2 = 29,25;
(b0)2 = 20,25;
b0 = ±4,5.
В ответе требуется записать меньшее из значений b0.
Ответ: -4,5.
Задача. Даны векторы \( \vec{a}\ \)(4; -1) и \( \vec{b}\ \)(b0; 8). Найдите b0, если |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите большее из них.
Решение.
Найдём модуль вектора \( \vec{a}\ \)(4; -1).
\( | \vec{a}|=\sqrt{4^2+(-1)^2}\ \);
\( | \vec{a}|=\sqrt{17}\ \).
Найдём модуль вектора \( \vec{b}\ \)(b0; 8).
\( | \vec{b}|=\sqrt{(b_0)^2+8^2}\ \);
\( | \vec{b}|=\sqrt{(b_0)^2+64}\ \);
По условию |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.
Получаем b2 = 6,25a2.
(b0)2 + 64 = 6,25 ∙ 17;
(b0)2 + 64 = 106,25;
(b0)2 = 42,25;
b0 = ±6,5.
В ответе требуется записать большее из значений b0.
Ответ: 6,5.
Задача. Даны векторы \( \vec{a}(-1; 3)\ \), \( \vec{b}(4; 1)\ \), \( \vec{c}(2; c_0)\ \). Найдите с0, если \( ( \vec{a}+\vec{b})\: \cdot \: \vec{c} =0\ \).
Решение.

Скалярное произведение векторов равно сумме произведение соответственных координат этих векторов.

3 ∙ 2 + 4 ∙ с0 = 0;
с0 = -6 : 4;
с0 = -1,5.
Ответ: -1,5.
Задача. Даны векторы \( \vec{a}(3; -1)\ \), \( \vec{b}(2; 0)\ \), \( \vec{c}(4; c_0)\ \). Найдите с0, если \( ( \vec{a}- \vec{b})\: \cdot \: \vec{c} =0\ \).
Решение аналогично решению предыдущей задачи.

1 ∙ 4 + (-1) ∙ с0 = 0;
-с0 = -4;
с0 = 4.
Ответ: 4.
Задача. Даны векторы \( \vec{a}(-2; 4)\ \)и \( \vec{b}(2; -1)\ \). Известно, что векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправленные, а \( | \vec{c}|=| \vec{a}|\ \). Найдите хс+ус.
Решение.

Так как длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправлены, то и координаты вектора \( \vec{c}(x_c; y_c)\ \) больше координат вектора \( \vec{b}\ \) в два раза.
Получаем хс = 2 ∙ 2 = 4 и ус = -1 ∙ 2 = -2.
Тогда хс + ус = 4 + (-2) = 2.
Ответ: 2.
Задача. Даны векторы \( \vec{a}(4; -6)\ \)и \( \vec{b}(-2; 3)\ \). Известно, что \( | \vec{c}|=| \vec{a}|\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) противоположно направленные. Найдите хс+ус.
Решение аналогично решению предыдущей задачи.
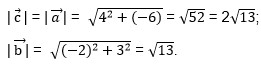
Длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \), по условию, противоположно направлены, следовательно отношение координат вектора \( \vec{c}(x_c; y_c)\ \) к соответственным координатам вектора \( \vec{b}\ \) равно (-2).
Получаем хс = -2 ∙ (-2) = 4 и ус = -2 ∙ 3 = -6.
Тогда хс + ус = 4 + (-6) = -2.
Ответ: -2.
Каждую из двух предыдущих задач можно решить быстро и легко графическим способом.
Смотрите видео.
Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}\ \), если \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). В ответ запишите сумму координат вектора \( \vec{c}\ \).
Решение.
Определим координаты данных векторов.
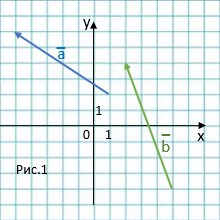

Каждая координата вектора равна разности соответствующих координат его конца и начала.
Смотрим рис. 2.
А1(1; 2) и А2(-5; 6); В1(5; -4) и В2(2; 4). Тогда

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
![]()
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
По условию \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). Следовательно,
![]()
Таким образом, сумма координат вектора \( \vec{c}\ \) равна 4,5.
Ответ: 4,5.
Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}(x_c; y_c)\ \), если \( \vec{c}=\vec{a}-1,5 \vec{b}\ \).
В ответ запишите произведение хс ∙ ус.
Решение аналогично решению предыдущей задачи.

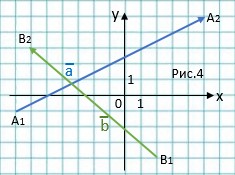
Определим координаты данных векторов.
Смотрим рис. 4.
А1(-7; -1) и А2(5; 5); В1(2; -4) и В2(-6; 3). Тогда

По условию \( \vec{c}=\vec{a}-1,5 \vec{b}\ \). Следовательно,
![]()
Таким образом, искомое произведение координат вектора \( \vec{c}\ \)
хс ∙ ус = 24 ∙ (- 4,5) = -108.
Ответ: -108.
Задача. Даны векторы \( \vec{a}(4; y_a)\ \)и \( \vec{b}(x_b; 0)\ \), косинус угла между которыми равен \( \frac{2}{\sqrt{5}}\ \). Найдите уа. Если таких значений несколько, в ответ запишите большее из них.
Решение.
Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла φ между ними.
![]()
В прямоугольной системе координат скалярное произведение векторов
\( \vec{a}(x_1; y_1)\ \)и \( \vec{b}(x_2; y_2)\ \) выражается формулой
\( \vec{a} \cdot \vec{b} =x_1x_2+y_1y_2\ \)
Получаем равенство:
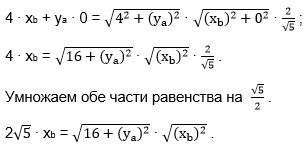
Возведём обе части равенства в квадрат:
20 ∙ (xb)2 = (16 + (ya)2) ∙ (xb)2; делим на (xb)2 обе части равенства:
20 = 16 + (уа)2;
(уа)2 = 4;
уа = ±2.
Большее из этих значений уа = 2.
Ответ: 2.
Задача. Даны векторы \( \vec{a}(x_a; -2)\ \)и \( \vec{b}(0; y_b)\ \), косинус угла между которыми равен \( -\sqrt{0,2}\ \). Найдите xа. Если таких значений несколько, в ответ запишите меньшее из них.
Решение аналогично решению предыдущей задачи.
Составим равенство на основании формулы:
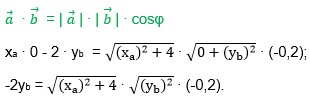
Разделим обе части равенства на (-0,2).
![]()
Возведём обе части равенства в квадрат:
20 ∙ (уb)2 = ((хa)2 + 4) ∙ (уb)2; делим на (уb)2 обе части равенства:
20 = (ха)2 + 4;
(ха)2 = 16;
ха = ±4.
Меньшее из этих значений ха = -4.
Ответ: -4.
Задача. Даны векторы \( \vec{a}(14; -2)\ \)и \( \vec{b}(-7; -1)\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Решение.
Найдём модули данных векторов.

Получаем:
14 ∙ (-7) + (-2) ∙ (-1) = 10 ∙ 5 ∙ cosα;
-98 + 2 = 100 ∙ cosα, отсюда cosα = -0,96.
Ответ: -0,96.
Задача. Даны векторы \( \vec{a}(-6; 2)\ \)и \( \vec{b}(9; 13)\ \). Найдите косинус угла между
векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Решение аналогично решению предыдущей задачи.
Находим модули данных векторов.

Получаем:
-6 ∙ 9 + 2 ∙ 13 = 2 ∙ 5 ∙ cosα;
-54 + 26 = 100 ∙ cosα;
-54 + 26 = 100 ∙ cosα;
-28 = 100 ∙ cosα;
отсюда cosα = -0,28.
Ответ: -0,28.
Как найти скалярное произведение векторов
Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите скалярное произведение векторов \( \vec{a}\ \)и \( 2\vec{b}\ \).
Решение.
Скалярным произведением векторов
\( \vec{a}\ \){a1; a2} и \( \vec{b}\ \){b1; b2}
называется число a1b1 + a2b2.
Произведением вектора \( \vec{a}\ \){a1; a2} на число λ называется вектор \( λ\vec{a}\ \){λa1; λa2}.
Пусть вектор \( \vec{a}\ \)имеет началом точку
А1(х1; у1), а концом – точку А2(х2; у2).
Координатами вектора \( \vec{a}\ \) будем называть числа а1 = х2 -х1, а2 = у2 -у1.


У нас (см. рис.2) А1(-2; 5), А2(-6; -4).
Тогда \( \vec{a}(-4; -9)\ \).
Так как В1(6; 2), В2(1; -2), то \( \vec{b}\ \){-5; -4}.
Следовательно, \( 2\vec{b}(-10; -8)\ \).
Итак, искомое скалярное произведение
\( \vec{a}\ \)и \( 2\vec{b}\ \):
\( \vec{a}\ \)∙ \( 2\vec{b}\ \)= -4 ∙ (-10) + (-9) ∙ (-8) = 40 + 72 = 112.
Ответ: 112.
Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите скалярное произведение векторов \( 2\vec{a}\ \)и \( \vec{b}\ \).


Решение.
У нас (см. рис.4) А1(-6; 4), А2(-2; -2).
Тогда \( \vec{a}\ \){4; -6} и \( 2\vec{a}\ \){8; -12}.
Начало и конец вектора \( \vec{b}\ \) – точки В1(-1; -4) и В2(2; 3),
следовательно, \( \vec{b}\ \){3; 7}.
Итак, искомое скалярное произведение
\( 2\vec{a}\ \)и \( \vec{b}\ \):
\( 2\vec{a}\ \)∙ \( \vec{b}\ \)= 8 ∙ 3 + (-12) ∙ 7 = 24 -84 = -60.
Ответ: -60.
Задача. Даны векторы \( \vec{a}\ \)(2; -5) и \( \vec{b}\ \)(5; 7). Найдите скалярное произведение векторов \( 0,6\vec{a}\ \)и \(1,4\vec{b}\ \).
Решение.
\( 0,6\vec{a}\ \)(0,6 ∙ 2; 0,6 ∙ (-5)); \( 0,6\vec{a}\ \)(1,2; -3).
\( 1,4\vec{b}\ \)(1,4 ∙ 5; 1,4 ∙ 7); \( 1,4\vec{b}\ \)(7; 9,8).
Скалярное произведение этих векторов
\( 0,6\vec{a}\ \)∙ \(1,4\vec{b}\ \) = 1,2 ∙ 7 + (-3) ∙ 9,8 = 8,4 -29,4 = -21.
Ответ: -21.
Задача. Даны векторы \( \vec{a}\ \)(2,2; -4) и
\( \vec{b}\ \)(-1,25; -1). Найдите скалярное произведение векторов \( 3\vec{a}\ \)и \(4\vec{b}\ \).
Решение.
Искомое скалярное произведение векторов
\( 3\vec{a}\ \)∙ \(4\vec{b}\ \) = 12\( \vec{a}\ \)∙ \( \vec{b}\ \) = 12(2,2 ∙ (-1,25) + (-4) ∙ (-1)) =
= 12(-2,75 + 4) = 12 ∙ 1,25 = 15.
Ответ: 15.
Задача. На координатной плоскости (рис.5) изображены векторы \( \vec{a}\ \), \( \vec{b}\ \)и \( \vec{c}\ \). Найдите скалярное произведение \( \vec{a}\ \)∙ \( (\vec{b}+\vec{c})\ \).
Решение.
Мы знаем, что скалярное произведение двух векторов равно сумме произведений соответственных координат этих координат.
Сумму векторов \( \vec{b}\ \) и \( \vec{c}\ \) заменим вектором \( \vec{d}\ \).
Найдём координаты векторов \( \vec{a}\ \)и \( \vec{d}\ \).
Смотрим рис. 6.


А1(-1; -2) и А2(-7; 3). Тогда \( \vec{a}\ \){-6; 5}.
B1(5; -4) и B2(5; 1). Тогда \( \vec{b}\ \){0; 5}.
C1(1; 4) и C2(-6; -1). Тогда \( \vec{c}\ \){-7; -5}.
При сложении двух векторов, складываются соответственные координаты этих векторов.
Так как \( \vec{d}\ \)= \( \vec{b}\ \)+\( \vec{c}\ \), то \( \vec{d}\ \){-7; 0}. Тогда искомое скалярное произведение:
\( \vec{a}\ \)∙ \( ( \vec{b}+\vec{c})\ \)= \( \vec{a}\ \)∙ \( \vec{d}\ \) = -6 ∙ (-7) + 5 ∙ 0 = 42.
Ответ: 42.
Задача. На координатной плоскости (рис.7) изображены векторы \( \vec{a}\ \), \( \vec{b}\ \)и \( \vec{c}\ \). Найдите скалярное произведение \( \vec{a}\ \)∙ \( (3 \vec{a}- 2 \vec{b})\ \).
Решение.
Применим распределительный закон умножения векторов.
\( \vec{a}\ \)∙ \( (3 \vec{b}- 2 \vec{c})\ \)= \( 3\vec{a}\ \) ∙ \( \vec{b}\ \)- \( 2\vec{a}\ \) ∙ \( \vec{c}\ \).
Найдём скалярные произведения векторов: \( \vec{a}\ \)и \( \vec{b}\ \); \( \vec{a}\ \)и \( \vec{c}\ \).
Определим координаты всех трёх векторов.
Смотрим рисунок 8.


А1(-2; -1) и А2(-7; 3). Тогда \( \vec{a}\ \){-5; 4}.
B1(3; -1) и B2(6; 4). Тогда \( \vec{b}\ \){3; 5}.
C1(2; 5) и C2(-2; 2). Тогда \( \vec{c}\ \){-4; -3}.
Тогда
\( \vec{a}\ \)∙ \( \vec{b}\ \)= -5 ∙ 3 + 4 ∙ 5 = -15 + 20 = 5;
\( \vec{a}\ \)∙ \( \vec{c}\ \)= -5 ∙ (-4) + 4 ∙ (-3) = 20 -12 = 8.
Искомое скалярное произведение векторов
\( \vec{a}\ \)∙ \( (3 \vec{b}- 2 \vec{c})\ \)= \( 3\vec{a}\ \) ∙ \( \vec{b}\ \)- \( 2\vec{a}\ \) ∙ \( \vec{c}\ \)= 3 ∙ 5 -2 ∙ 8 = 15 -16 = -1.
Ответ: -1.
Задача. Вычислите скалярное произведение векторов \( \vec{a}\ \) и \( \vec{b}\ \),
если |\( \vec{a}\ \)| = 3, |\( \vec{b}\ \)| = 4, а угол между ними равен 60°.
Решение.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
\( \vec{a}\ \) ∙ \( \vec{b}\ \)= |\( \vec{a}\ \)| ∙ |\( \vec{b}\ \)| ∙ cosφ,
где φ – угол между векторами \( \vec{a}\ \) и \( \vec{a}\ \).
Получаем
\( \vec{a}\ \) ∙ \( \vec{b}\ \)= 3 ∙ 4 ∙ cos60° = 12 ∙ 0,5 = 6.
Ответ: 6.
Задача. Вычислите скалярное произведение векторов
\( \vec{p}\ \) = \( \vec{a}\ \)- \( \vec{b}\ \)- \( \vec{c}\ \) и \( \vec{q}\ \) = \( \vec{a}\ \)- \( \vec{b}\ \)+\( \vec{c}\ \),
если |\( \vec{a}\ \)| = 5, |\( \vec{b}\ \)| = 2, |\( \vec{c}\ \)| = 4 и \( \vec{a} \perp \vec{b}\ \).
Решение.
\( \vec{p}\ \) ∙ \( \vec{q}\ \)= (\( \vec{a}\ \)- \( \vec{b}\ \)-\( \vec{c}\ \)) ∙ (\( \vec{a}\ \)- \( \vec{b}\ \)+\( \vec{c}\ \))=
= \( \vec{a}\ \)2-\( \vec{a}\ \)∙ \( \vec{b}\ \)-\( \vec{a}\ \)∙ \( \vec{c}\ \)-\( \vec{a}\ \) ∙ \( \vec{b}\ \)+\( \vec{b}\ \)2+\( \vec{b}\ \) ∙ \( \vec{c}\ \)+\( \vec{a}\ \) ∙ \( \vec{c}\ \)-\( \vec{b}\ \) ∙ \( \vec{c}\ \)-\( \vec{c}\ \)2 =
= |\( \vec{a}\ \)|2+|\( \vec{b}\ \)|2-|\( \vec{c}\ \)|2-\(2 \vec{a}\ \)∙ \( \vec{b}\ \)= 52 + 22 -42 -0 =
= 25 + 4 -16 = 13.
Скалярное произведение двух взаимно перпендикулярных векторов равно нулю.
Так как у нас по условию \( \vec{a} \perp \vec{b}\ \), то \( \vec{a}\ \) ∙ \( \vec{b}\ \)= 0.
Ответ: 13.
Задача. Вычислите скалярное произведение векторов \( \vec{a}\ \)и \( \vec{b}\ \),
если \( \vec{a}\ \)= 3\( \vec{p}\ \) -2\( \vec{q}\ \) и \( \vec{b}\ \)= \( \vec{p}\ \)+ 4\( \vec{q}\ \), где \( \vec{p}\ \)и \( \vec{q}\ \) – единичные взаимно перпендикулярные векторы.
Решение.
\( \vec{a}\ \)∙ \( \vec{b}\ \)= (3\( \vec{p}\ \) -2\( \vec{q}\ \))(\( \vec{p}\ \)+ 4\( \vec{q}\ \)) = 3\( \vec{p}\ \)2 -2\( \vec{p}\ \)∙ \( \vec{q}\ \)+ 12\( \vec{p}\ \)∙ \( \vec{q}\ \) -8\( \vec{q}\ \)2 =
= 3|\( \vec{p}\ \)|2 +10\( \vec{p}\ \)∙ \( \vec{q}\ \) -8|\( \vec{q}\ \)|2 = 3 ∙ 1 + 10 · 0 -8 ∙ 1 = -5.
Ответ: -5.
Задача. Даны точки А(1; 3; 0), B(2; 3; -1),
C(1; 2; -1). Найдите скалярное произведение
векторов \( \vec{AB}\ \) и \( \vec{AC}\ \).
Решение.
Так как скалярное произведение векторов равно сумме произведений соответственных координат этих векторов, то найдём эти координаты.
\( \vec{AB}\ \){2-1; 3-3; -1-0} → \( \vec{AB}\ \){1; 0; -1};
\( \vec{AC}\ \){1-1; 2-3; -1-0} → \( \vec{AC}\ \){0; -1; -1}.
\( \vec{AB}\ \) ∙ \( \vec{AC}\ \) = 1 ∙ 0 + 0 ∙ (-1) + (-1) ∙ (-1) = 1.
Ответ: 1.
Как найти косинус угла между векторами, изображёнными на координатной плоскости
Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите cosα,
Найдите cosα,
где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
1 способ решения – традиционный.
Применим формулу \( cos \alpha=\frac{ \vec{a}\: \cdot\: \vec{b}}{| \vec{a}|\: \cdot\:| \vec{b}|}\ \) ( * )
Здесь \( \vec{a}\: \cdot\: \vec{b}\ \)- скалярное произведение векторов \( \vec{a}\ \)и \( \vec{b}\ \), которое равно сумме произведений соответственных координат этих векторов.
Требуется найти координаты и модули данных векторов. 
Для вектора \( \vec{a}\ \)координаты начала А1(-1; -4) и конца А2(-4; 2).
Тогда абсцисса вектора \( \vec{a}\ \)равна -4-(-1) = -3; ордината 2-(-4) = 6.
Вектор \( \vec{a}\ \){-3; 6}, модуль вектора \( \vec{a}\ \):
\( | \vec{a}|=\sqrt{(-3)^2+6^2}\ \)= \( \sqrt{9+36}\ \)= \( \sqrt{45}\ \)= \( 3\sqrt{5}\ \).
Для вектора \( \vec{b}\ \)координаты начала В1(-3; 5) и конца В2(5; 1).
Тогда абсцисса вектора \( \vec{b}\ \) равна 5-(-3) = 8; ордината 1-5 = -4.
Вектор \( \vec{b}\ \){8; -4}, модуль вектора \( \vec{b}\ \):
\( | \vec{b}|=\sqrt{8^2+(-4)^2}\ \)= \( \sqrt{64+16}\ \)= \( \sqrt{80}\ \)= \( 4\sqrt{5}\ \).
Все найденные значения подставляем в формулу ( * ):
\( cos \alpha=\frac{-3\: \cdot\:8\:+\:6\: \cdot\:(-4)}{3\sqrt{5}\ \cdot \:4\sqrt{5}}\ \);
\( cos \alpha=\frac{-48}{12\: \cdot\:5 }\ \);
\( cos \alpha=-\frac{4}{5}\ \);
cosα = -0,8.
Ответ: -0,8.
2 способ решения – нас не будут интересовать координаты векторов.
Выберем точку с целыми координатами на векторе \( \vec{a}\ \).
Пусть это будет точка М(-3; 0). Отложим от этой точки вектор \( \vec{MN}\ \), сонаправленный вектору \( \vec{b}\ \) так, чтобы точка N имела целые координаты. Достроим треугольник АМN.


Сторона АМ этого треугольника – это гипотенуза прямоугольного треугольника с катетами 2 и 1.
АМ2 = 22 + 12 = 4 + 1= 5;
\( AM=\sqrt{5}\ \).
Сторона МN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 4 и 2.
МN2 = 42 + 22 = 16 + 4 = 20;
\( MN=\sqrt{20}\ \) или \( MN=2\sqrt{5}\ \).
Сторона АN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 5 и 4.
АN2 = 52 + 42 = 25 + 16 = 41;
\( AN=\sqrt{41}\ \).
Искомый угол АМТ обозначим через α
На основании теоремы косинусов
\( cos \alpha=\frac{AM^2+MN^2-AN^2}{2 \cdot AM\: \cdot\:MN}\ \);
\( cos \alpha=\frac{5+20-41}{2\sqrt{5}\: \cdot\:2\sqrt{5}}\ \);
\( cos \alpha=-\frac{16}{4\: \cdot\:5 }\ \);
\( cos \alpha=-\frac{4}{5}\ \);
cosα = -0,8.
Ответ: -0,8.
Ещё одна задача.
Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Смотрим видео.
На координатной плоскости изображены векторы а, b и с
Задача. На координатной плоскости изображены векторы
![]()

Решение.
Пусть А1(-7; 6) и А2(-3; 3) – начало и конец
![]()
Пусть В1(2; 1) и В2(2; 5) – начало и конец
![]()
Пусть C1(4; -4) и C2(-4; -2) – начало и конец

Ответ: 5.
Эту задачу на сложение данных векторов можно решить графически, используя правило многоугольника. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.



![]()


Длина (модуль) этого вектора равна 5. Это гипотенуза прямоугольного треугольника с катетами 3 и 4.
Ответ: 5.
Смотрим видео.
Задача. На координатной плоскости изображены векторы
![]()
Смотрим видео.
В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы: каждый январь долг увеличивается на 10%
Задача. В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:
-каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
-с февраля по июнь необходимо выплатить одним платежом часть долга;
-в июле 2026, 2027, 2028, 2029 и 2030 долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
-в июле 2030 года долг должен составлять 800 тысяч рублей;
-в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же сумму меньше долга на июль предыдущего года;
Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.
Решение. Пусть в каждый из первых пяти лет долг будет уменьшаться на х тыс. рублей. Так как через эти 5 лет долг должен составлять 800 тыс. рублей, то первоначальный кредит равен (5х+800). С этой суммы посчитаем все проценты, которые будут начислены банком в первые 5 лет:
0,1(5х+800 + 4х+800 + 3х+800 + 2х+800 + х+800) =
= 0,1 ∙ 15х + 0,1 ∙ 800 ∙ 5 = 1,5х + 400 (тыс. руб.).
С июля 2030 года долг должен составлять 800 тысяч рублей по условию. Погашать его нужно будет следующие 5 лет на одну и ту же сумму. Мы легко определим эту сумму. Делим 800 на 5 и получаем 160 тысяч рублей. Однако, для удобства подсчёта процентов за последние 5 лет, обозначим эту сумму через у. Итак,
у=160, значит, долг 800=5у. Считаем проценты:
0,1(5у+4у+3у+2у+у) = 0,1 ∙ 15у = 1,5у.
Заменяем у на 160 и получаем 1,5 ∙ 160 = 240 тысяч рублей – проценты за последние 5 лет.
Таким образом, за всё время кредитования клиент выплатит:
(5х + 800) тыс. руб. — данную банком сумму;
(1,5х + 400) тыс. руб. — проценты за первые 5 лет;
240 тыс. руб. — проценты за последние 5 лет.
По условию сумма выплат по кредиту равна 2090 тысяч рублей. Получаем уравнение:
5х + 800 + 1,5х + 400 + 240 = 2090. Решаем:
6,5х = 2090-1440;
6,5х = 650;
х = 100.
На 100 тыс. руб. будет уменьшаться долг ежегодно в первые 5 лет.
А так как взятую сумму кредита мы обозначали через (5х+800) тысяч рублей, то она составит 5 ∙ 100 + 800 = 1300 тысяч рублей.
Ответ: 1300000 рублей.
15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы: 1-го числа каждого месяца долг возрастает на 3%
Задача. 15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
Решение. Для удобства обозначим через х величину, на которую ежемесячно уменьшался долг первые 10 месяцев (х = 80 тыс. рублей), а через у – остаток долга на 11 месяц кредитования (долг 15 числа 10-го месяца). Тогда, очевидно, что кредит был равен (10х + у) тысяч рублей.
Подсчитаем проценты за первые 10 месяцев.
0,03 ∙ ( (10х+у) + (9х+у) + (8х+у) + … + (х+у)) =
= 0,03 ∙ (10х + 9х + 8х +…+ х) + 0,03 ∙ 10у =
= 0,03 ∙ 55х + 0,3у = 1,65х + 0,3у.
За 11-й месяц будет выплачено (у + 0,03у) тыс. рублей.
Итак, за всё время кредитования клиент заплатил
10х + 1,65х + 0,3у + у + 0,03у или 1198 тыс. рублей.
10х – это 80 ∙ 10 = 800 тысяч рублей.
800 + 1,65х + 1,33у = 1198;
1,65 ∙ 80 + 1,33у = 1198-800;
132 + 1,33у = 398;
1,33у = 398-132;
1,33у = 266;
у = 200.
Ответ: 200 тысяч рублей.
В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей.
Задача. В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей. Условия его возврата таковы:
-в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
-в период с февраля по сентябрь необходимо выплатить часть долга;
-в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же величину Q рублей меньше долга на октябрь предыдущего года;
-в 2033 и 2034 годах выплаты по кредиту равны;
-к октябрю 2034 года кредит должен быть полностью погашен.
Найдите величину Q, если общая сумма выплат по кредиту должна составить 4168 тыс. рублей.
Решение.
Пусть ежегодно в первые 5 лет долг будет уменьшаться на Q тыс. рублей (не рублей, а тысяч рублей). Посчитаем сумму процентов, которые будут выплачены за эти 5 лет:
0,15 ∙ (2560 + (2560-Q) + (2560-2Q) + (2560-3Q) + (2560-4Q)) =
= 0,15 ∙ (5 ∙ 2560-10Q) = (1920-1,5Q) тыс. рублей.
Следовательно, за первые 5 лет общие выплаты составят
5Q + 1920-1,5Q = (3,5Q + 1920) тыс. рублей. Остаток долга станет равным
(2560-5Q) тыс. рублей (ежегодно будут списывать только Q тыс. рублей).
Обозначим эту сумму (остаток долга) через S.
S = 2560-5Q. Эта сумма будет выплачена в 2033 и 2034 годах двумя равными платежами – обозначим каждый такой платёж через Y. Как это будет происходить?
Банк увеличит сумму долга на 15% — получится 115% от S, т.е 1,15S.
Клиент платит Y тыс. рублей, и долг станет равным (1,15S-Y) тыс. рублей.
Банк начисляет на эту сумму 15% — долг составит 1,15(1,15S-Y).
Клиент выплачивает Y тыс. рублей, и долг обнулится, т.е. мы имеем равенство:
1,15 ∙ (1,15S -Y)-Y = 0.
1,152 ∙ S -1,15Y-Y = 0
1,3225S -1,15Y -Y = 0
2,15Y = 1,3225S.
А так как S = (2560-5Q), то 2,15Y = 1,3225(2560-5Q). Выразим Y.
![]()
Так как Y – это платёж в каждый из двух последних лет кредитования, то за 2 последних года банку будет выплачено 2Y тыс. рублей.
Общие выплаты за все 7 лет составят:
3,5Q + 1920 + 2Y или 4168 тыс. рублей.
3,5Q + 1920 + 2Y = 4168;
3,5Q + 2Y = 4168-1920;
3,5Q + 2Y = 2248;
Подставим вместо Y его значение и решим уравнение относительно Q.
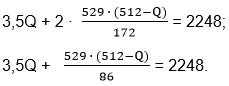
Умножаем обе части равенства на 86.
301Q + 529(512-Q) = 193328;
301Q + 270848 -529Q = 193328;
301Q -529Q = 193328 -270848;
-228Q = -77520;
Q = 340. Мы нашли Q в тысячах рублей, ответ нужно дать в рублях.
Ответ: 340000 рублей.
В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей.
Задача. В октябре 2027 года Анна планирует взять кредит в банке на 7 лет в размере 4350 тыс. рублей. Условия его возврата таковы:
-в январе каждого года действия кредита долг увеличивается на 10% от суммы долга на конец предыдущего года;
-в период с февраля по сентябрь необходимо выплатить часть долга;
-в октябре каждого года в первые пять лет действия кредита (2028 – 2032 гг.) долг должен быть на одну и ту же сумму меньше долга на октябрь предыдущего года;
-в 2033 и 2034 годах выплаты по кредиту равны;
-к октябрю 2034 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат по кредиту должна составить 6025 тыс. рублей. Сколько рублей составит выплата 2031 года?
Решение.
Пусть ежегодно в первые 5 лет долг будет уменьшаться на х тыс. рублей. Посчитаем сумму процентов, которые будут выплачены за эти 5 лет:
0,1 ∙ (4350 + (4350-х) + (4350-2х) + (4350-3х) + (4350-4х)) =
= 0,1 ∙ (5 ∙ 4350-10х) = (2175-х) тыс. рублей.
Следовательно, за первые 5 лет общие выплаты составят
5х + 2175-х = (4х + 2175) тыс. рублей. Остаток долга станет равным
(4350-5х) тыс. рублей (ежегодно будут списывать только х тыс. рублей).
Обозначим эту сумму (остаток долга) через S.
S = 4350-5x. Эта сумма будет выплачена в 2033 и 2034 годах двумя равными платежами – обозначим каждый такой платёж через Y. Как это будет происходить?
Банк увеличит сумму долга на 10% — получится 110% от S, т.е 1,1S.
Клиент платит Y тыс. рублей, и долг станет равным (1,1S-Y) тыс. рублей.
Банк начисляет на эту сумму 10% — долг составит 1,1(1,1S-Y).
Клиент выплачивает Y тыс. рублей, и долг обнулится, т.е. мы имеем равенство:
1,1 ∙ (1,1S -Y)-Y = 0.
1,12 ∙ S -1,1Y-Y = 0
1,21S -1,1Y -Y = 0
2,1Y = 1,21S.
А так как S = (4350-5х), то 2,1Y = 1,21(4350-5x). Выразим Y.
![]()
Так как Y – это платёж в каждый из двух последних лет кредитования, то за 2 последних года банку будет выплачено 2Y тыс. рублей.
Общие выплаты за все 7 лет составят:
4х + 2175 + 2Y или 6025 тыс. рублей.
4х + 2175 + 2Y = 6025;
4х + 2Y = 6025-2175;
4х + 2Y = 3850;
2х + Y = 1925.
Подставим вместо Y его значение и решим уравнение относительно х.
![]()
Умножаем обе части равенства на 42.
84х + 121(870-х) = 80850;
84х + 105270-121х = 80850;
84х -121х = 80850 -105270;
-37х = -24420;
х = 660.
Итак, на х или 660 тысяч рублей долг будет уменьшаться ежегодно в первые 5 лет.
За 2031 год выплата составит х + 0,1(4350-3х) = 0,7х+435. Так как х=660, то получим
0,7 ∙ 660 + 435 = 462 + 435 = 897 (тыс. рублей)
Ответ: 897 тысяч рублей.
В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей
Задача. В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 15% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2033, 2034, 2035, 2036 и 2037 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2037 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2400 тыс. рублей. Сколько рублей составит платёж в 2029 году?
Решение.
Условие «-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
15% банк насчитывает на остаток долга.
0,15 ∙ (1500 + (1500-х) + (1500-2х) + (1500-3х) + (1500-4х)) =
= 0,15 ∙ (5 ∙ 1500 -10х) = 0,15(7500-10х) = (1125-1,5х) тыс. рублей.
Итак, к концу 2032 года (после 5 лет ежегодных выплат) долг составит (1500-5х) тыс. рублей или 5(300-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (300-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,15 ∙ (5(300-х) + 4(300-х) + 3(300-х) + 2(300-х) + (300-х)) =
= 0,15 ∙ 15(300-х) = 2,25 ∙ (300-х) = (675-2,25х) тыс. рублей.
По условию общая сумма выплат 2400 тыс. рублей, значит, сумма выплаченных процентов составит 2400-1500 = 900 тыс. рублей. Составим уравнение.
1125-1,5х + 675-2,25х = 900;
-1,5х-2,25х = 900-1125-675;
-3,75х = -900 | : (-3,75);
х = 240. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 240 тыс. рублей.
Искомый платёж за 2029 год составит эти 240 тыс. рублей плюс 15% от остатка долга, т.е. от суммы 1500-240 = 1260 тыс. рублей, так как в 2028 году уже было погашено 240 тыс. рублей.
Считаем: 240 + 0,15 ∙ 1260 = 240 + 189 = 429 тыс. рублей.
Ответ: 429000 рублей.
Задача. В июле 2026 года планируется взять кредит на 10 лет в размере 1300 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2032, 2033, 2034, 2035 и 2036 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2036 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2780 тыс. рублей. Сколько рублей составит платёж в 2027 году?
Решение.
Условие «-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
20% банк насчитывает на остаток долга.
0,2 ∙ (1300 + (1300-х) + (1300-2х) + (1300-3х) + (1300-4х)) =
= 0,2 ∙ (5 ∙ 1300 -10х) = 0,2(6500-10х) = (1300-2х) тыс. рублей.
Итак, к концу 2031 года (после 5 лет ежегодных выплат) долг составит (1300-5х) тыс. рублей или 5(260-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (260-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,2 ∙ (5(260-х) + 4(260-х) + 3(260-х) + 2(260-х) + (260-х)) =
= 0,2 ∙ 15(260-х) = 3 ∙ (260-х) = (780-3х) тыс. рублей.
По условию общая сумма выплат 2780 тыс. рублей, значит, сумма выплаченных процентов составит 2780-1300 = 1480 тыс. рублей. Составим уравнение.
1300-2х + 780-3х = 1480;
-2х-3х = 1480-1300-780;
-5х = -600 | : (-5);
х = 120. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 120 тыс. рублей.
Искомый платёж за 2027 год составит эти 120 тыс. рублей плюс 20% от взятой суммы кредита в 1300 тыс. рублей, так как в 2027 году состоится самая первая выплата банку.
Считаем: 120 + 0,2 ∙ 1300 = 120 + 260 = 380 тыс. рублей.
Ответ: 380000 рублей.
На одной полке стоит 36 блюдец: 14 синих и 22 красных
Задача. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Решение. Будем брать 1 блюдце с первой полки и 1 чашку со второй полки, затем снова 1 блюдце с первой полки и 1 чашку со второй полки. Необходимо получить 2 чайные (одного цвета) пары. Подойдут следующие случаи:
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
Рассмотрим вероятность наступления каждого из этих случаев.
1)блюдце и чашка, блюдце и чашка — берём синее блюдце с первой полки (любое из 14, а всего 36 блюдец) и синюю чашку со второй полки (любую из 27, а всего 36 чашек), затем берём синее блюдце с первой полки (любое из 13, а всего 35 блюдец) и синюю чашку со второй полки (любую из 26, а всего 35 чашек). Эти 4 события независимы друг от друга, поэтому, вероятность их одновременного наступления равна произведению вероятностей выбора каждого из предметов:


Ответ: 0,29.
Задача. На одной полке стоит 25 блюдец: 16 красных и 9 синих. На другой полке стоит 25 чашек: 13 красных и 12 синих. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Решение. Будем брать 1 блюдце с первой полки и 1 чашку со второй полки, затем снова 1 блюдце с первой полки и 1 чашку со второй полки. Необходимо получить 2 чайные (одного цвета) пары. Подойдут следующие случаи:
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка;
блюдце и чашка, блюдце и чашка.
Рассмотрим вероятность наступления каждого из этих случаев.
1) блюдце и чашка, блюдце и чашка – берём синее блюдце с первой полки (любое из 9, а всего 25 блюдец) и синюю чашку со второй полки (любую из 12, а всего 25 чашек), затем берём синее блюдце с первой полки (любое из 8, а всего 24 блюдец) и синюю чашку со второй полки (любую из 11, а всего 24 чашек). Эти 4 события независимы друг от друга, поэтому, вероятность их одновременного наступления равна произведению вероятностей выбора каждого из предметов:

Искомая вероятность p = p1 + p2 + p3 + p4 + p5 + p6.

Ответ: 0,38.


