Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС
Задача. Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1, пересекаются в одной точке.
б) Известно, что АВ=АС=17 и ВС=16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Решение.
Так как точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС, то отрезки А1В1, В1С1 и А1С1 являются средними линиями треугольника АВС (рис. 1).
Средняя линия треугольника параллельна третьей стороне и равна её половине.
Вследствие этого мы получаем 4 треугольника, равных между собой по трём сторонам. Нас будут интересовать 3 из них (окрашены).

Около каждого из этих треугольников описана окружность.
Центр окружности, описанной около любого треугольника – это точка пересечения серединных перпендикуляров к сторонам треугольника.
Пусть точка О1 – центр окружности (рис. 2), описанной около ΔА1СВ1 – пересечение серединных перпендикуляров О1Х и О1Х1 к сторонам А1С и В1С;
точка О2 – центр окружности, описанной около ΔА1ВС1 – пересечение серединных перпендикуляров О2Y и О2Y1 к сторонам А1B и ВС1. Заметим также, что точки Х, А1 и Y делят ВС на 4 равных отрезка.
точка О3 – центр окружности, описанной около ΔB1AC1 – пересечение серединных перпендикуляров О3Z и О3Z1 к сторонам АB1 и AC1; Заметим также, что точки Х1, В1 и Z делят AС на 4 равных отрезка, a точки Y1, C1 и Z1 делят AB на 4 равных отрезка.
а) Около равных треугольников А1СВ1 и A1BC1 будут описаны равные окружности, которые пересекаются в точках А1 и М (рис. 3).

Общая хорда А1М перпендикулярна линии центров О1О2 и проходит через точку К – середину отрезка О1О2. Следовательно, А1М будет осью симметрии для этих окружностей и является серединным перпендикуляром к отрезку ВС.
Итак, А1М Ʇ О1О2 и А1М Ʇ ВС, значит, О1О2 || BC.
В прямоугольнике ХО1О2Y О1О2 = XY, поэтому, очевидно, что О1О2 = ½ ВС.
Аналогично, прямая, проходящая через точки пересечения окружностей с центрами О1 и О3 (рис. 4), будет являться серединным перпендикуляром к стороне АС треугольника АВС, и О1О3 || AC и О1О3 = ½ АС.
Точно так же прямая, проходящая через точки пересечения окружностей с центрами О2 и О3 будет являться серединным перпендикуляром к стороне АВ треугольника АВС, и О2О3 || AВ и О2О3 = ½АВ.
Как известно, серединные перпендикуляры к сторонам любого треугольника пересекаются в одной точке, поэтому все три окружности пересекаются в точке М, ч.т.д. Точка М – центр окружности, описанной около треугольника АВС.
б) Так как длины сторон треугольника О1О2О3 равны соответственно половинам сторон треугольника АВС, то Δ О1О2О3 подобен ΔАВС по трём пропорциональным сторонам с коэффициентом подобия 1/2. Следовательно, радиус окружности, вписанной в треугольник О1О2О3 будет равен половине радиуса окружности, вписанной в треугольник АВС.
Радиус окружности, вписанной в ΔАВС найдём по формуле:
![]()
 По условию АВ=АС=17 и ВС=16 (рис. 5). Проведём высоту AA1.
По условию АВ=АС=17 и ВС=16 (рис. 5). Проведём высоту AA1.
В равнобедренном ΔАВС высота AA1 – медиана, поэтому, в прямоугольном ΔAА1B гипотенуза АВ=17, катет ВA1=8, тогда второй катет AA1=15 (пифагорова «тройка» 8, 15, 17 или примените теорему Пифагора).
Тогда 2S = ВС ∙ AA1 = 16 ∙ 15 = 240.
Периметр ΔАВС равен 17+17+16 = 50.
Тогда r = 240 : 50 = 4,8.
Искомый радиус вписанной окружности для Δ О1О2О3 равен половине найденного радиуса вписанной окружности для ΔАВС, делим 4,8 пополам и получаем 2,4.
Ответ: 2,4. Смотреть видео решение.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС
Задача. Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со всеми сторонами трапеции составляет 12/49 площади трапеции ABCD.
Решение.
 а) По условию трапеция ABCD с основаниями AD и ВС описана около окружности с центром О, следовательно, точка О есть пересечение биссектрис всех углов трапеции. Так как сумма углов трапеции, прилегающих к боковой стороне АВ, равна 180°, то сумма половинок этих углов равна 90°. Таким образом в ΔАОВ
а) По условию трапеция ABCD с основаниями AD и ВС описана около окружности с центром О, следовательно, точка О есть пересечение биссектрис всех углов трапеции. Так как сумма углов трапеции, прилегающих к боковой стороне АВ, равна 180°, то сумма половинок этих углов равна 90°. Таким образом в ΔАОВ
∠OАB + ∠АВО = 90°, значит, и ∠АОВ = 90°.
Аналогично, так как ∠BCD + ∠ADC = 180°, то в ΔСOD
∠OCD + ∠ODC = 90°, следовательно, и ∠COD = 90°. Доказано.
б) По условию равнобедренная трапеция ABCD с основаниями AD и ВС описана около окружности с центром О. Пусть эта окружность касается сторон трапеции в точках М, Р, N и К. Четырёхугольник MPNK является вписанным в данную окружность. Радиус, проведённый в точку касания перпендикулярен касательной.
Тогда ОМ⟘АВ, ОР⟘ВС, ОN⟘CD, ОK⟘АD. Смотреть видео решение этой задачи.
РК – диаметр окружности, перпендикулярен к основаниям трапеции и проходит через их середины, так как длины касательных, проведённых из одной точки к окружности, равны. РК – ось симметрии данной трапеции и четырёхугольника МРNК. Будем рассматривать половину данной трапеции слева от РК.

 Площадь Δ МРК состоит из суммы площадей двух равновеликих треугольников МОР и МОК.
Площадь Δ МРК состоит из суммы площадей двух равновеликих треугольников МОР и МОК.
Действительно, площадь каждого из них равна половине произведения двух сторон (радиусов окружности) на синус угла (с вершиной в точке О) между ними; значения синусов смежных углов равны.
Проведём ОВ. Это биссектриса угла В трапеции ABCD.
В равнобедренном треугольнике МВР биссектриса ВТ является и медианой, и высотой (Т – середина МР, ВТ⟘МР). Тогда медиана ОТ (высота и биссектриса) делит равнобедренный треугольник ОМР на два равных треугольника РТО и МТО.
Аналогично рассуждая относительно ОА – биссектрисы угла А трапеции ABCD, делаем вывод, что равны треугольники МЕО и КЕО. Половинки равновеликих треугольников МОР и МОК также равновелики (и равны), значит, треугольник МРК состоит из четырёх равных треугольников, поэтому, разделив его площадь на 4, получим:
![]()
Выделим эти треугольники жёлтым цветом.
Итак, в рассматриваемой прямоугольной трапеции АВРК остаются:
Δ ВТР = Δ ВТМ (закрасим зелёным цветом) и
Δ АЕК = Δ АЕМ (закрасим розовым цветом).
Сумма этих четырёх, попарно равных треугольников, равна
![]()
Делим это значение пополам. Получаем:
![]()
В задаче требуется найти отношение AD : BC.
Обозначим AD = a, BC = b.
Нам нужно найти значение a : b.
По свойству касательных, проведённых из одной точки к окружности:
![]()
ОМ –радиус окружности, проведённый в точку касания, является высотой в прямоугольном треугольнике АОВ. По свойству пропорциональных отрезков в прямоугольном треугольнике

РТ – высота прямоугольного треугольника ВРО, проведённая к гипотенузе ВО, делит треугольник ВРО на подобные треугольники ВТР и РТО с коэффициентом подобия, равным отношению сходственных сторон:
![]()
Отношение площадей подобных треугольников равно квадрату их коэффициента подобия.

Точно так же, КЕ – высота прямоугольного Δ АКО, проведённая к гипотенузе АО, делит этот треугольник на подобные треугольники АЕК и КЕО. Тогда коэффициент их подобия:

6 + 6t2 = 37t;
6t2 -37t + 6 = 0. Решаем квадратное уравнение по общей формуле.
D = 372 -4 ∙ 6 ∙ 6 = 1369 -144 = 1225 = 352;

Итак, AD : BC = 6.
Ответ: 6.
Фигуры на клетчатой бумаге с размером клетки 1х1
Рассмотрим задачи по нахождению элементов и площадей треугольников и четырёхугольников по их изображениям на клетчатой бумаге. Такие задачи по силам и восьмиклассникам, а предлагаются выпускникам на ЕГЭ. Ниже приведены (с решениями) прототипы задачи 3 из ЕГЭ.
Задача 1. На клетчатой бумаге изображён прямоугольный треугольник. Найдите его площадь.
Площадь прямоугольного треугольника равна половине произведения его катетов.

Задача 2. На клетчатой бумаге изображён треугольник. Найдите его площадь.
Площадь любого треугольника равна половине произведения его основания на высоту, проведённую к этому основанию.

Задача 3. Найдите площадь треугольника, изображённого на клетчатой бумаге.
Для нахождения площади данного треугольника АВС, можно из площади прямоугольника МКРС вычесть площади прямоугольных треугольников АМС, АКВ и ВРС.

Задача 4. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольник.
Найдите: а) диагональ прямоугольника; б) площадь прямоугольника; в) радиус описанной окружности.

а) Находим диагональ АС. Из прямоугольного треугольника АВС по теореме Пифагора
АС2 = АВ2 + ВС2 = 32 + 42 = 9 + 16 = 25.
АС = 5.
б) Площадь прямоугольника ABCD находим по формуле:
S = ab; S = AB ∙ BC = 3 ∙ 4 = 12.
в) диаметром окружности, описанной около прямоугольника ABCD, является диагональ АС. Следовательно, радиус описанной окружности R = АС : 2 = 5 : 2 = 2,5.
Ответ: а) 5; б) 12; в) 2,5.
Задача 5. На клетчатой бумаге с размером клетки 1х1 изображён квадрат. Найдите площадь квадрата.

Площадь квадрата S = AB2. По теореме Пифагора из прямоугольного треугольника АВС:
АВ2 = АС2 + ВС2 = 22 + 42 = 4 + 16 = 20. Ответ: S = 20.
Задача 6. На клетчатой бумаге с размером клетки 1х1 изображён квадрат.
Найдите: а) площадь квадрата; б) радиус описанной окружности.
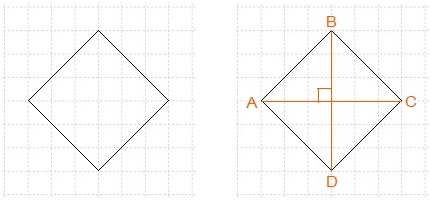
а) Площадь квадрата равна половине произведения его диагоналей.
У нас диагонали АС = BD = 6.
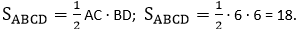
б) Центр окружности, описанной около квадрата есть точка пересечения его диагоналей. Следовательно, искомый радиус R = 3.
Ответ: S = 18; R = 3.
Задача 7. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм.
Найдите: а) площадь параллелограмма;
б) большую высоту параллелограмма.
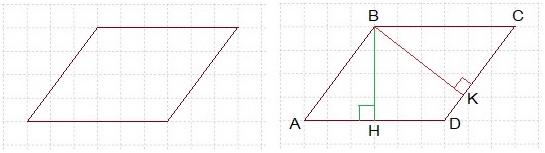
а) Площадь параллелограмма равна произведению его основания на высоту, проведённую к этому основанию.
S = AD ∙ BH = 6 ∙ 4 = 24.
б) Проведём высоту ВК. Из прямоугольного треугольника АНВ
с катетами АН = 3 и ВН = 4 по теореме Пифагора находим гипотенузу АВ=5.
CD = AB = 5. Итак, стороны параллелограмма АD = 6 и CD = 5. Сторона
CD – меньшая, значит высота ВК, проведённая к ней, является большей.
S = CD ∙ BK;
24 = 5 ∙ BK;
BK = 24 : 5 = 4,8. Ответ: S = 24; BK = 4,8.
Задача 8. На клетчатой бумаге с размером клетки 1х1 изображён ромб.
Найдите: а) площадь ромба;
б) радиус вписанной окружности.
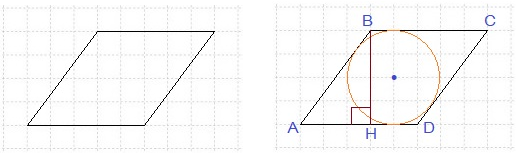
а) Площадь ромба S = AD ∙ BH, где AD – основание, ВН – высота ромба.
S = 6 ∙ 4 = 24.
б) Окружность вписана в ромб. Её диаметр равен высоте ромба ВН.
Так как диаметр окружности равен 4, то радиус r = 2.
Ответ: S = 24; r = 2.
Задача 9. Найти площадь ромба, изображённого на клетчатой бумаге.

Диагонали ромба пересекаются под прямым углом.
Площадь ромба равна половине произведения его диагоналей.

Задача 10. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите: длину средней линии и площадь этой трапеции.
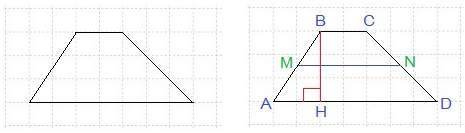
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции.
MN – средняя линия.
Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Площадь трапеции равна произведению полусуммы её оснований на высоту трапеции.

Ответ: MN=4,5; S=13,5.
Задача 11. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 30. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры – это площадь кольца, которую мы найдём как разность площадей данных кругов с общим центром.
Пусть R -радиус большего круга, r – радиус меньшего круга.
Все круги подобны.
Площади подобных фигур относятся как квадраты их соответствующих линейных размеров.
У нас R : r = 3 : 2, а площадь меньшего круга радиуса r равна 30.

Отсюда площадь заштрихованной фигуры равна: