Найдите все значения а, при каждом из которых система уравнений имеет более 2-х решений

Задача. Найдите все значения а, при каждом из которых система уравнений имеет более двух решений.

Решение. Рассмотрим первое уравнение системы.

Раскроем модульные скобки.

Определим знак каждого подмодульного выражения.  Для этого воспользуемся методом интервалов.

а) x²-2х=х(х-2). x²-2х≥0 на промежутках (-∞; 0]U[2; +∞);

x²-2х<0 на промежутке (0; 2).

б) у²-2у≥0 на промежутках (-∞; 0]U[2; +∞); у²-2у<0 на промежутке (0; 2).

В зависимости от знака подмодульного выражения мы можем получить 4 разных уравнения.

1) Если x²-2х≥0 и у²-2у≥0, т.е. если

х∈(-∞; 0]U[2; +∞) и у∈(-∞; 0]U[2; +∞), то после раскрытия модульных скобок мы получаем равенство:

х²+х²-2х=у²+у²-2у    →  2х²-2х=2у²-2у    →   х²-х=у²-у   →   (х²-у²)-(х-у)=0;

(х-у)(х+у)-(х-у)=0   →   (х-у)(х+у-1)=0.

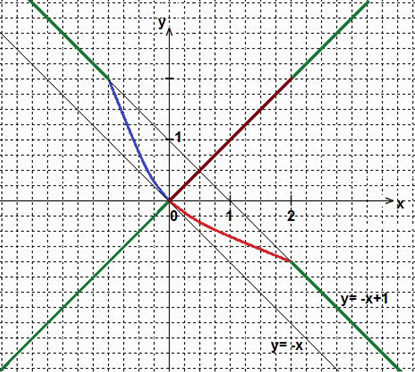
Отсюда следует, что либо х-у=0, либо х+у-1=0, поэтому графиком этого уравнения будут служить точки, лежащие на прямых у=х и у= -х+1. Построим  эти прямые на участках координатной плоскости для

х∈(-∞; 0]U[2; +∞) и у∈(-∞; 0]U[2; +∞). Линии изобразим зеленым цветом. Смотрите координатную плоскость.

2) Если x²-2х<0 и у²-2у<0, т.е. если х∈(0; 2) и у∈(0; 2), то выражения в модульных скобках перепишем с противоположными знаками и получим:

х²-х²+2х=у²-у²+2у    →  у=х. График – прямая, которая является биссектрисой I и III-го координатных углов. Изобразим коричневым цветом только отрезок этой прямой при

х (0; 2) и у (0; 2).

3) Если x²-2х≥0 и у²-2у<0, т.е. если х∈(-∞; 0]U[2; +∞) и у∈(0; 2), то получаем уравнение

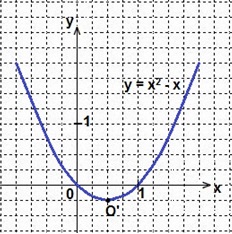
х²+х²-2х= у²-у²+2у    →  2у=2х²-2х  →  у=х²-х. Это квадратичная функция. Графиком служит парабола, пересекающая ось Ох в

точках (0; 0) и (2; 0), ветви параболы направлены вверх.

Вершина параболы O’(m; n), где m= -b : (2a) = 1 : 2 = 0,5;

n=у(m) = у(0,5)=0,5²-0,5=0,25-0,5=-0,25. Синим цветом начертим часть этой параболы, точки которой удовлетворяют условиям:

х∈(-∞; 0]U[2; +∞) и у∈(0; 2).

4) Если x²-2х<0 и у²-2у≥0, т.е.

если х∈(0; 2) и у∈(-∞; 0]U[2; +∞), то после раскрытия модульных скобок мы получаем равенство:

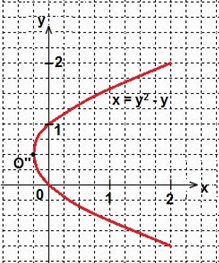
х²-х²+2х=у²+у²-2у   →  2х=2у²-2у  →   х=у²-у. Это квадратичная функция зависимости х от у. Эта парабола пересекает ось Оу в

точках (0; 0) и (0; 2). Вершина параболы

O”(m; n), m= -b : (2a) = 1 : 2 = 0,5;

n=x(m) = x(0,5)=0,5²-0,5=0,25-0,5=-0,25. Так как функция у нас зависит от переменной у, то координаты вершины параболы х= -0,25, у=0,5.

Чертим красным цветом ту часть параболы, точки которой удовлетворяют условиям:

х∈(0; 2) и у∈(-∞; 0]U[2; +∞).

Данная система уравнений должна иметь более двух решений, поэтому необходимо, чтобы прямая х + у = а пересекала построенный нами график  более чем в двух точках. Запишем это уравнение в виде у = -х +а. График функции у = -х есть биссектриса II и IV-го координатных углов и имеет одну общую точку с графиком первого уравнения. Если этот график сдвинуть на один единичный отрезок вверх, то прямая  у = -х +1 будет иметь множество общих точек с графиком первого уравнения (смотрите 1 пункт решения нашего задания), следовательно система будет иметь множество решений.

Вывод: при значениях  0< а ≤ 1 прямая у = -х + а будет иметь с графиком первого уравнения более двух общих точек. Ответ: 0< а ≤ 1.