Задания на векторы в 1 части профильного ЕГЭ по математике
Задача. Даны векторы \( \vec{a}\ \)(2; 3) и \( \vec{b}\ \)(-3; b0). Найдите b0, если |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите меньшее из них.
Решение.
Модуль вектора \( \vec{a}\ \)(а1; а2) равен квадратному корню из суммы квадратов его координат:
\( | \vec{a}|=\sqrt{(a_1)^2+(a_2)^2}\ \);
\( | \vec{a}|=\sqrt{2^2+3^2}\ \); \( | \vec{a}|=\sqrt{13}\ \).
Найдём модуль вектора \( \vec{b}\ \)(-3; b0).
\( | \vec{b}|=\sqrt{(-3)^2+(b_0)^2}\ \);
\( | \vec{b}|=\sqrt{9+(b_0)^2}\ \).
По условию |\( \vec{b}\ \)| = 1,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.
Получаем b2 = 2,25a2.
9 + (b0)2 = 2,25 ∙ 13;
9 + (b0)2 = 29,25;
(b0)2 = 20,25;
b0 = ±4,5.
В ответе требуется записать меньшее из значений b0.
Ответ: -4,5.
Задача. Даны векторы \( \vec{a}\ \)(4; -1) и \( \vec{b}\ \)(b0; 8). Найдите b0, если |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Если таких значений несколько, в ответ запишите большее из них.
Решение.
Найдём модуль вектора \( \vec{a}\ \)(4; -1).
\( | \vec{a}|=\sqrt{4^2+(-1)^2}\ \);
\( | \vec{a}|=\sqrt{17}\ \).
Найдём модуль вектора \( \vec{b}\ \)(b0; 8).
\( | \vec{b}|=\sqrt{(b_0)^2+8^2}\ \);
\( | \vec{b}|=\sqrt{(b_0)^2+64}\ \);
По условию |\( \vec{b}\ \)| = 2,5|\( \vec{a}\ \)|. Возведём обе части равенства в квадрат.
Получаем b2 = 6,25a2.
(b0)2 + 64 = 6,25 ∙ 17;
(b0)2 + 64 = 106,25;
(b0)2 = 42,25;
b0 = ±6,5.
В ответе требуется записать большее из значений b0.
Ответ: 6,5.
Задача. Даны векторы \( \vec{a}(-1; 3)\ \), \( \vec{b}(4; 1)\ \), \( \vec{c}(2; c_0)\ \). Найдите с0, если \( ( \vec{a}+\vec{b})\: \cdot \: \vec{c} =0\ \).
Решение.
Скалярное произведение векторов равно сумме произведение соответственных координат этих векторов.
3 ∙ 2 + 4 ∙ с0 = 0;
с0 = -6 : 4;
с0 = -1,5.
Ответ: -1,5.
Задача. Даны векторы \( \vec{a}(3; -1)\ \), \( \vec{b}(2; 0)\ \), \( \vec{c}(4; c_0)\ \). Найдите с0, если \( ( \vec{a}- \vec{b})\: \cdot \: \vec{c} =0\ \).
Решение аналогично решению предыдущей задачи.
1 ∙ 4 + (-1) ∙ с0 = 0;
-с0 = -4;
с0 = 4.
Ответ: 4.
Задача. Даны векторы \( \vec{a}(-2; 4)\ \)и \( \vec{b}(2; -1)\ \). Известно, что векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправленные, а \( | \vec{c}|=| \vec{a}|\ \). Найдите хс+ус.
Решение.
Так как длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) сонаправлены, то и координаты вектора \( \vec{c}(x_c; y_c)\ \) больше координат вектора \( \vec{b}\ \) в два раза.
Получаем хс = 2 ∙ 2 = 4 и ус = -1 ∙ 2 = -2.
Тогда хс + ус = 4 + (-2) = 2.
Ответ: 2.
Задача. Даны векторы \( \vec{a}(4; -6)\ \)и \( \vec{b}(-2; 3)\ \). Известно, что \( | \vec{c}|=| \vec{a}|\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \) противоположно направленные. Найдите хс+ус.
Решение аналогично решению предыдущей задачи.
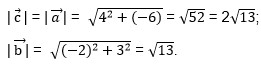
Длина вектора \( \vec{c}(x_c; y_c)\ \)вдвое больше длины вектора \( \vec{b}\ \), а векторы \( \vec{c}(x_c; y_c)\ \)и \( \vec{b}\ \), по условию, противоположно направлены, следовательно отношение координат вектора \( \vec{c}(x_c; y_c)\ \) к соответственным координатам вектора \( \vec{b}\ \) равно (-2).
Получаем хс = -2 ∙ (-2) = 4 и ус = -2 ∙ 3 = -6.
Тогда хс + ус = 4 + (-6) = -2.
Ответ: -2.
Каждую из двух предыдущих задач можно решить быстро и легко графическим способом.
Смотрите видео.
Задача. На координатной плоскости (рис.1) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}\ \), если \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). В ответ запишите сумму координат вектора \( \vec{c}\ \).
Решение.
Определим координаты данных векторов.
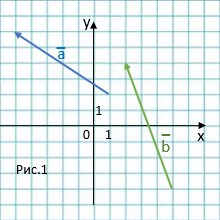
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Смотрим рис. 2.
А1(1; 2) и А2(-5; 6); В1(5; -4) и В2(2; 4). Тогда
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
По условию \( \vec{c}=0,5 \vec{b}- \vec{a}\ \). Следовательно,
Таким образом, сумма координат вектора \( \vec{c}\ \) равна 4,5.
Ответ: 4,5.
Задача. На координатной плоскости (рис.3) изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите координаты вектора \( \vec{c}(x_c; y_c)\ \), если \( \vec{c}=\vec{a}-1,5 \vec{b}\ \).
В ответ запишите произведение хс ∙ ус.
Решение аналогично решению предыдущей задачи.
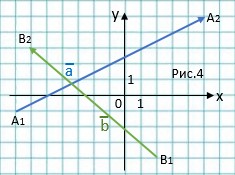
Определим координаты данных векторов.
Смотрим рис. 4.
А1(-7; -1) и А2(5; 5); В1(2; -4) и В2(-6; 3). Тогда
По условию \( \vec{c}=\vec{a}-1,5 \vec{b}\ \). Следовательно,
Таким образом, искомое произведение координат вектора \( \vec{c}\ \)
хс ∙ ус = 24 ∙ (- 4,5) = -108.
Ответ: -108.
Задача. Даны векторы \( \vec{a}(4; y_a)\ \)и \( \vec{b}(x_b; 0)\ \), косинус угла между которыми равен \( \frac{2}{\sqrt{5}}\ \). Найдите уа. Если таких значений несколько, в ответ запишите большее из них.
Решение.
Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла φ между ними.
В прямоугольной системе координат скалярное произведение векторов
\( \vec{a}(x_1; y_1)\ \)и \( \vec{b}(x_2; y_2)\ \) выражается формулой
\( \vec{a} \cdot \vec{b} =x_1x_2+y_1y_2\ \)
Получаем равенство:
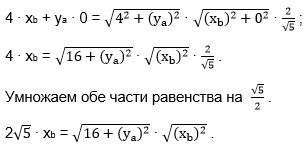
Возведём обе части равенства в квадрат:
20 ∙ (xb)2 = (16 + (ya)2) ∙ (xb)2; делим на (xb)2 обе части равенства:
20 = 16 + (уа)2;
(уа)2 = 4;
уа = ±2.
Большее из этих значений уа = 2.
Ответ: 2.
Задача. Даны векторы \( \vec{a}(x_a; -2)\ \)и \( \vec{b}(0; y_b)\ \), косинус угла между которыми равен \( -\sqrt{0,2}\ \). Найдите xа. Если таких значений несколько, в ответ запишите меньшее из них.
Решение аналогично решению предыдущей задачи.
Составим равенство на основании формулы:
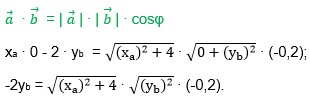
Разделим обе части равенства на (-0,2).
Возведём обе части равенства в квадрат:
20 ∙ (уb)2 = ((хa)2 + 4) ∙ (уb)2; делим на (уb)2 обе части равенства:
20 = (ха)2 + 4;
(ха)2 = 16;
ха = ±4.
Меньшее из этих значений ха = -4.
Ответ: -4.
Задача. Даны векторы \( \vec{a}(14; -2)\ \)и \( \vec{b}(-7; -1)\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Решение.
Найдём модули данных векторов.
Получаем:
14 ∙ (-7) + (-2) ∙ (-1) = 10 ∙ 5 ∙ cosα;
-98 + 2 = 100 ∙ cosα, отсюда cosα = -0,96.
Ответ: -0,96.
Задача. Даны векторы \( \vec{a}(-6; 2)\ \)и \( \vec{b}(9; 13)\ \). Найдите косинус угла между
векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Решение аналогично решению предыдущей задачи.
Находим модули данных векторов.
Получаем:
-6 ∙ 9 + 2 ∙ 13 = 2 ∙ 5 ∙ cosα;
-54 + 26 = 100 ∙ cosα;
-54 + 26 = 100 ∙ cosα;
-28 = 100 ∙ cosα;
отсюда cosα = -0,28.
Ответ: -0,28.
Как найти косинус угла между векторами, изображёнными на координатной плоскости
Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \).
Найдите cosα,
где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
1 способ решения – традиционный.
Применим формулу \( cos \alpha=\frac{ \vec{a}\: \cdot\: \vec{b}}{| \vec{a}|\: \cdot\:| \vec{b}|}\ \) ( * )
Здесь \( \vec{a}\: \cdot\: \vec{b}\ \)- скалярное произведение векторов \( \vec{a}\ \)и \( \vec{b}\ \), которое равно сумме произведений соответственных координат этих векторов.
Требуется найти координаты и модули данных векторов. 
Для вектора \( \vec{a}\ \)координаты начала А1(-1; -4) и конца А2(-4; 2).
Тогда абсцисса вектора \( \vec{a}\ \)равна -4-(-1) = -3; ордината 2-(-4) = 6.
Вектор \( \vec{a}\ \){-3; 6}, модуль вектора \( \vec{a}\ \):
\( | \vec{a}|=\sqrt{(-3)^2+6^2}\ \)= \( \sqrt{9+36}\ \)= \( \sqrt{45}\ \)= \( 3\sqrt{5}\ \).
Для вектора \( \vec{b}\ \)координаты начала В1(-3; 5) и конца В2(5; 1).
Тогда абсцисса вектора \( \vec{b}\ \) равна 5-(-3) = 8; ордината 1-5 = -4.
Вектор \( \vec{b}\ \){8; -4}, модуль вектора \( \vec{b}\ \):
\( | \vec{b}|=\sqrt{8^2+(-4)^2}\ \)= \( \sqrt{64+16}\ \)= \( \sqrt{80}\ \)= \( 4\sqrt{5}\ \).
Все найденные значения подставляем в формулу ( * ):
\( cos \alpha=\frac{-3\: \cdot\:8\:+\:6\: \cdot\:(-4)}{3\sqrt{5}\ \cdot \:4\sqrt{5}}\ \);
\( cos \alpha=\frac{-48}{12\: \cdot\:5 }\ \);
\( cos \alpha=-\frac{4}{5}\ \);
cosα = -0,8.
Ответ: -0,8.
2 способ решения – нас не будут интересовать координаты векторов.
Выберем точку с целыми координатами на векторе \( \vec{a}\ \).
Пусть это будет точка М(-3; 0). Отложим от этой точки вектор \( \vec{MN}\ \), сонаправленный вектору \( \vec{b}\ \) так, чтобы точка N имела целые координаты. Достроим треугольник АМN.
Сторона АМ этого треугольника – это гипотенуза прямоугольного треугольника с катетами 2 и 1.
АМ2 = 22 + 12 = 4 + 1= 5;
\( AM=\sqrt{5}\ \).
Сторона МN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 4 и 2.
МN2 = 42 + 22 = 16 + 4 = 20;
\( MN=\sqrt{20}\ \) или \( MN=2\sqrt{5}\ \).
Сторона АN этого треугольника – это гипотенуза прямоугольного треугольника с катетами 5 и 4.
АN2 = 52 + 42 = 25 + 16 = 41;
\( AN=\sqrt{41}\ \).
Искомый угол АМТ обозначим через α
На основании теоремы косинусов
\( cos \alpha=\frac{AM^2+MN^2-AN^2}{2 \cdot AM\: \cdot\:MN}\ \);
\( cos \alpha=\frac{5+20-41}{2\sqrt{5}\: \cdot\:2\sqrt{5}}\ \);
\( cos \alpha=-\frac{16}{4\: \cdot\:5 }\ \);
\( cos \alpha=-\frac{4}{5}\ \);
cosα = -0,8.
Ответ: -0,8.
Ещё одна задача.
Задача. На координатной плоскости изображены векторы \( \vec{a}\ \)и \( \vec{b}\ \). Найдите cosα, где α – угол между векторами \( \vec{a}\ \)и \( \vec{b}\ \).
Смотрим видео.
Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС
Задача. Точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1, пересекаются в одной точке.
б) Известно, что АВ=АС=17 и ВС=16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Решение.
Так как точки А1, В1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС, то отрезки А1В1, В1С1 и А1С1 являются средними линиями треугольника АВС (рис. 1).
Средняя линия треугольника параллельна третьей стороне и равна её половине.
Вследствие этого мы получаем 4 треугольника, равных между собой по трём сторонам. Нас будут интересовать 3 из них (окрашены).
Около каждого из этих треугольников описана окружность.
Центр окружности, описанной около любого треугольника – это точка пересечения серединных перпендикуляров к сторонам треугольника.
Пусть точка О1 – центр окружности (рис. 2), описанной около ΔА1СВ1 – пересечение серединных перпендикуляров О1Х и О1Х1 к сторонам А1С и В1С;
точка О2 – центр окружности, описанной около ΔА1ВС1 – пересечение серединных перпендикуляров О2Y и О2Y1 к сторонам А1B и ВС1. Заметим также, что точки Х, А1 и Y делят ВС на 4 равных отрезка.
точка О3 – центр окружности, описанной около ΔB1AC1 – пересечение серединных перпендикуляров О3Z и О3Z1 к сторонам АB1 и AC1; Заметим также, что точки Х1, В1 и Z делят AС на 4 равных отрезка, a точки Y1, C1 и Z1 делят AB на 4 равных отрезка.
а) Около равных треугольников А1СВ1 и A1BC1 будут описаны равные окружности, которые пересекаются в точках А1 и М (рис. 3).
Общая хорда А1М перпендикулярна линии центров О1О2 и проходит через точку К – середину отрезка О1О2. Следовательно, А1М будет осью симметрии для этих окружностей и является серединным перпендикуляром к отрезку ВС.
Итак, А1М Ʇ О1О2 и А1М Ʇ ВС, значит, О1О2 || BC.
В прямоугольнике ХО1О2Y О1О2 = XY, поэтому, очевидно, что О1О2 = ½ ВС.
Аналогично, прямая, проходящая через точки пересечения окружностей с центрами О1 и О3 (рис. 4), будет являться серединным перпендикуляром к стороне АС треугольника АВС, и О1О3 || AC и О1О3 = ½ АС.
Точно так же прямая, проходящая через точки пересечения окружностей с центрами О2 и О3 будет являться серединным перпендикуляром к стороне АВ треугольника АВС, и О2О3 || AВ и О2О3 = ½АВ.
Как известно, серединные перпендикуляры к сторонам любого треугольника пересекаются в одной точке, поэтому все три окружности пересекаются в точке М, ч.т.д. Точка М – центр окружности, описанной около треугольника АВС.
б) Так как длины сторон треугольника О1О2О3 равны соответственно половинам сторон треугольника АВС, то Δ О1О2О3 подобен ΔАВС по трём пропорциональным сторонам с коэффициентом подобия 1/2. Следовательно, радиус окружности, вписанной в треугольник О1О2О3 будет равен половине радиуса окружности, вписанной в треугольник АВС.
Радиус окружности, вписанной в ΔАВС найдём по формуле:
По условию АВ=АС=17 и ВС=16 (рис. 5). Проведём высоту AA1.
В равнобедренном ΔАВС высота AA1 – медиана, поэтому, в прямоугольном ΔAА1B гипотенуза АВ=17, катет ВA1=8, тогда второй катет AA1=15 (пифагорова «тройка» 8, 15, 17 или примените теорему Пифагора).
Тогда 2S = ВС ∙ AA1 = 16 ∙ 15 = 240.
Периметр ΔАВС равен 17+17+16 = 50.
Тогда r = 240 : 50 = 4,8.
Искомый радиус вписанной окружности для Δ О1О2О3 равен половине найденного радиуса вписанной окружности для ΔАВС, делим 4,8 пополам и получаем 2,4.
Ответ: 2,4. Смотреть видео решение.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС
Задача. Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со всеми сторонами трапеции составляет 12/49 площади трапеции ABCD.
Решение.
а) По условию трапеция ABCD с основаниями AD и ВС описана около окружности с центром О, следовательно, точка О есть пересечение биссектрис всех углов трапеции. Так как сумма углов трапеции, прилегающих к боковой стороне АВ, равна 180°, то сумма половинок этих углов равна 90°. Таким образом в ΔАОВ
∠OАB + ∠АВО = 90°, значит, и ∠АОВ = 90°.
Аналогично, так как ∠BCD + ∠ADC = 180°, то в ΔСOD
∠OCD + ∠ODC = 90°, следовательно, и ∠COD = 90°. Доказано.
б) По условию равнобедренная трапеция ABCD с основаниями AD и ВС описана около окружности с центром О. Пусть эта окружность касается сторон трапеции в точках М, Р, N и К. Четырёхугольник MPNK является вписанным в данную окружность. Радиус, проведённый в точку касания перпендикулярен касательной.
Тогда ОМ⟘АВ, ОР⟘ВС, ОN⟘CD, ОK⟘АD. Смотреть видео решение этой задачи.
РК – диаметр окружности, перпендикулярен к основаниям трапеции и проходит через их середины, так как длины касательных, проведённых из одной точки к окружности, равны. РК – ось симметрии данной трапеции и четырёхугольника МРNК. Будем рассматривать половину данной трапеции слева от РК.
Площадь Δ МРК состоит из суммы площадей двух равновеликих треугольников МОР и МОК.
Действительно, площадь каждого из них равна половине произведения двух сторон (радиусов окружности) на синус угла (с вершиной в точке О) между ними; значения синусов смежных углов равны.
Проведём ОВ. Это биссектриса угла В трапеции ABCD.
В равнобедренном треугольнике МВР биссектриса ВТ является и медианой, и высотой (Т – середина МР, ВТ⟘МР). Тогда медиана ОТ (высота и биссектриса) делит равнобедренный треугольник ОМР на два равных треугольника РТО и МТО.
Аналогично рассуждая относительно ОА – биссектрисы угла А трапеции ABCD, делаем вывод, что равны треугольники МЕО и КЕО. Половинки равновеликих треугольников МОР и МОК также равновелики (и равны), значит, треугольник МРК состоит из четырёх равных треугольников, поэтому, разделив его площадь на 4, получим:
Выделим эти треугольники жёлтым цветом.
Итак, в рассматриваемой прямоугольной трапеции АВРК остаются:
Δ ВТР = Δ ВТМ (закрасим зелёным цветом) и
Δ АЕК = Δ АЕМ (закрасим розовым цветом).
Сумма этих четырёх, попарно равных треугольников, равна
Делим это значение пополам. Получаем:
В задаче требуется найти отношение AD : BC.
Обозначим AD = a, BC = b.
Нам нужно найти значение a : b.
По свойству касательных, проведённых из одной точки к окружности:
ОМ –радиус окружности, проведённый в точку касания, является высотой в прямоугольном треугольнике АОВ. По свойству пропорциональных отрезков в прямоугольном треугольнике
РТ – высота прямоугольного треугольника ВРО, проведённая к гипотенузе ВО, делит треугольник ВРО на подобные треугольники ВТР и РТО с коэффициентом подобия, равным отношению сходственных сторон:
Отношение площадей подобных треугольников равно квадрату их коэффициента подобия.
Точно так же, КЕ – высота прямоугольного Δ АКО, проведённая к гипотенузе АО, делит этот треугольник на подобные треугольники АЕК и КЕО. Тогда коэффициент их подобия:
6 + 6t2 = 37t;
6t2 -37t + 6 = 0. Решаем квадратное уравнение по общей формуле.
D = 372 -4 ∙ 6 ∙ 6 = 1369 -144 = 1225 = 352;
Итак, AD : BC = 6.
Ответ: 6.
В правильной треугольной призме на рёбрах АС и ВС отмечены соответствующие точки M и N
Задача.
В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответствующие точки M и N так, что AM : MC = CN : BN = 2 : 1,
точка К – середина ребра А1С1.
а) Докажите, что плоскость MNK проходит через вершину В1.
б) Найдите расстояние от точки С до плоскости KMN, если АВ = 6, АА1 = 2,4.
Решение.
а) В основании призмы лежит равносторонний треугольник АВС. Обозначим его сторону через а. Смотрите рис. 1.
Тогда АМ = 2а/3, МС = а/3 и
CN = 2а/3, BN = а/3.
А1К = КС1 = а/2.
Проведём MN и КМ. Это линии пересечения плоскости MNK с нижним основанием призмы и боковой гранью АА1С1С соответственно.
Проведём KF Ʇ AC, тогда AF = FC = a/2. А так как МС = а/3, то
MF = FC-MC = a/2-a/3 = a/6
Проведём В1K и BF.
Четырёхугольник BFKB1 является прямоугольником, отсюда В1K = BF.
В равностороннем треугольнике АВС медиана BF является и высотой.
Таким образом, BF Ʇ AC.
Имеем: MC : FC = a/3 : a/2 = 2 : 3 и CN : BC = 2a/3 : a = 2 : 3.
Треугольники MCN и FCB подобны по двум пропорциональным сторонам и общему углу С между ними. Соответственные углы подобных треугольников равны, поэтому прямые MN и BF параллельны по признаку параллельности прямых. Но BF и В1К параллельны, как противоположные стороны прямоугольника BFKB1, следовательно, параллельны и прямые MN и В1K.
Итак, плоскость MNK пересекает параллельные плоскости нижнего и верхнего основания по параллельным прямым MN и В1K, а так как через точку К можно провести единственную прямую параллельную данной, то очевидно, что плоскость MNK проходит через вершину В1, ч.т.д. Четырёхугольник MNB1K – плоскость сечения данной призмы.
б) Способ 1 (традиционный). Мы доказали, что прямые MN и BF параллельны,
а так как BF Ʇ АС, то и MN Ʇ АС. Для того, чтобы найти расстояние от точки С до плоскости KMN, определим плоскость, проходящую через точку С и перпендикулярную плоскости KMN. Проведём СК и рассмотрим плоскость МСК. Смотрите рис. 2.
На основании теоремы о трёх перпендикулярах MN Ʇ KM (MN – прямая, проведённая на плоскости через основание наклонной КМ, перпендикулярно её проекции FM).
Итак, MN Ʇ KM и MN Ʇ MC, следовательно, MN Ʇ (MCK). Плоскость MNK проходит через прямую MN, перпендикулярную плоскости MСK, а потому будет перпендикулярна плоскости MCK. Так как плоскость МСК перпендикулярна плоскости MNK и пересекает её по прямой МК, то расстоянием от точки С до плоскости KMN будет длина перпендикуляра, проведённого из точки С к прямой МК.
Треугольник МСК тупоугольный (угол СМК тупой, так как является смежным с острым углом KMF), поэтому точка Т — основание перпендикуляра СТ будет лежать на продолжении стороны МК треугольника МСК. Обозначим угол СМТ через α. Тогда и угол KMF равен α (вертикальные углы равны). В прямоугольном треугольнике СТM катет СТ = МС ∙ sinα,
где sinα = KF/MK из прямоугольного треугольника KFM.
По условию АВ = а = 6 и АА1 = 2,4.
Тогда МС = а/3 = 2; MF = a/6 = 1; KF = АА1 = 2,4.
Из прямоугольного треугольника KFM по теореме Пифагора
MK2 = MF2 + KF2 = 12 + 2,42 = 1 + 5,76 = 6,76. Отсюда MK = 2,6.
Получаем sinα = KF/MK = 2,4 : 2,6 = 12/13.
Искомый отрезок СТ = МС ∙ sinα = 2 ∙ 12/13 = 24/13. Это и есть расстояние от точки С до плоскости KMN.
Примечание. СТ можно было найти и без применения тригонометрии. Из подобия прямоугольных треугольников KFM и СТМ по острому углу α справедливо равенство
KF : CT = KM : MC, из которого и находим СТ.
Ответ: 24/13.
б) Способ 2 (метод координат в пространстве).
Решение.
Введём систему координат, считая точку F началом координат, a отрезки FC, FB и FK, лежащими соответственно на осях абсцисс, ординат и аппликат.
Смотрите рис. 3.
Точка М имеет координаты (1; 0; 0), так как MF = a/6 = 6 : 6 = 1.
Точка К имеет координаты (0; 0; 2,4), так как KF = АА1 = 2,4.
Точка С имеет координаты (3; 0; 0), так как FC = a/2 = 6 : 2 = 3.
Плоскость KMN параллельна оси Оу и отсекает от оси Ох отрезок равный 1, а от оси Оz отрезок, равный 2,4. Следовательно, плоскость KMN задаётся уравнением
которое равносильно уравнению 2,4x + z = 2,4 или 2,4x + z -2,4 = 0.
Требуется найти расстояние от точки С(3; 0; 0) до плоскости 2,4x + z -2,4 = 0.
Расстояние h от точки с координатами (xo; yo; zo)
до плоскости ax + by + cz + d = 0 определяется по формуле:
У нас х0 = 3, у0 = z0 = 0; а = 2,4; b = 0, c = 1, d = -2,4.
Тогда искомое расстояние от точки С до плоскости KMN:
Ответ: 24/13.
В правильной треугольной пирамиде МАВС
Задача. В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые рёбра равны 10. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ-точка L. Известно, что АD=АE=LМ=4.
а) Докажите, что отрезок DE содержит центр основания пирамиды.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
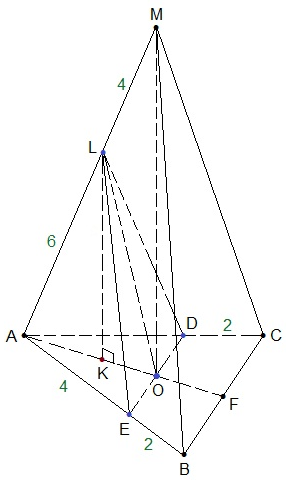Высота данной правильной пирамиды проектируется в центр правильного треугольника АВС – точку пересечения медиан (высот и биссектрис). Обозначим эту точку через О. Мы знаем, что эта точка (пересечения медиан) делит каждую медиану в отношении 2 : 1, считая от вершины, поэтому АО : ОЕ = 2 : 1, что равнозначно отношению АО : АF = 2 : 3. Проводим отрезки DE, DL и LE.
а) Так как DE отсекает от сторон АС и АВ равностороннего треугольника АВС отрезки по 4 см, то ∆ AED ∾ ∆ ABC по двум пропорциональным сторонам и углу между ними, ведь AD : AC = 2 : 3 (на самом деле, 4 : 6 = 2 : 3) и AE : AB = 2 : 3, и общему углу ВАС. Отсюда следует, что ∆AED тоже равносторонний и сторона его DE=AD=AE=4.
Соответствующие медианы подобных треугольников∆ AED и ∆ ABC тоже относятся как 2 : 3, а это и означает, что точка О лежит на отрезке DE.
б) Найдем площадь сечения пирамиды плоскостью, проходящей через точки E, D и L, иначе говоря, найдем площадь треугольника DEL. Проведем LO. В равнобедренном треугольнике DEL медиана LO является и высотой.
Мы знаем только, что DE= 4. Потребуется найти LO.
Проведем LK⟘AF. Прямоугольные треугольники AKL и AOM подобны по общему углу МАО. Справедливо равенство:
Итак, нам лишь потребуется найти МО-высоту пирамиды, которая является катетом в прямоугольном треугольнике АОМ.
Найдем АО, как радиус окружности, описанной около правильного треугольника АВС, по формуле:
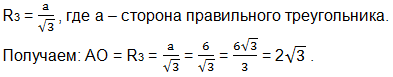
Из треугольника АОМ по теореме Пифагора:
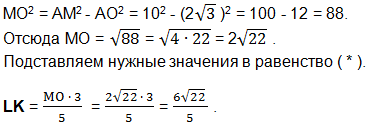
Значение ОК найдем как разность отрезков АО и АК.
Значение АК найдем также из подобия прямоугольных треугольников АОМ и АКL.
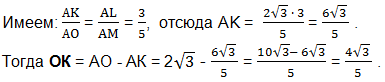
Из прямоугольного треугольника OКL по теореме Пифагора найдем LO.
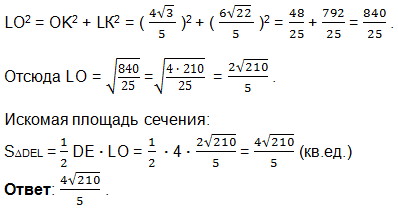
Радиус основания конуса с вершиной Р
Задача. Радиус основания конуса с вершиной Р равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1 : 5.
а) Постройте сечение конуса плоскостью, проходящей через точки А, В и Р.
б) Найдите площадь сечения конуса плоскостью АВР.
Решение.
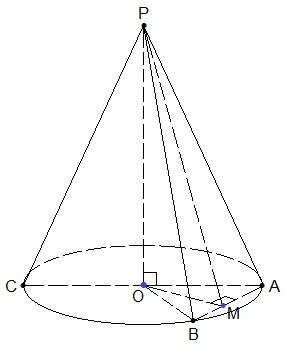
а) Пусть дан конус с осевым сечением РАС и высотой РО. Радиус основания конуса ОА=6, образующая PA=9. Через точки А, В и Р проведено сечение. Это ∆АВР. Так как точки А и В делят окружность на две дуги, длины которых относятся как 1 : 5, то дуга АВ составляет 1/6 часть длины окружности (всего 1+5=6 частей), и поэтому, центральный угол, соответствующий дуге АВ также составляет 1/6 часть угловой меры окружности.
Получается, что треугольник АОВ-равносторонний, и АВ=ОВ=ОА=6.
б) Проведем ОМ⟘АВ. Точка М-середина хорды АВ (радиус, перпендикулярный хорде делит её и стягиваемую ею дугу пополам).
Таким образом, АМ=ВМ=АВ : 2 = 6 : 2 = 3.
В равнобедренном треугольнике АВР с основанием АВ медиана РМ является и высотой. Площадь треугольника АВР равна половине произведения АВ на высоту треугольника РМ.
РМ-катет в прямоугольном ∆АМР. По теореме Пифагора:
РМ2 = РА2 -АМ2 = 92— 32 = 81- 27 = 72, отсюда
Искомая площадь сечения конуса плоскостью АВР:
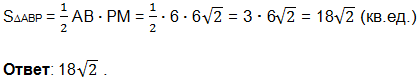
В треугольной пирамиде МАВС основанием является
Задача. В треугольной пирамиде МАВС основанием является правильный треугольник АВС, ребро МВ перпендикулярно плоскости основания, стороны основания равны 3, а ребро МА равно 5. На ребре Ас находится точка D, на ребре АВ находится точка Е, а на ребре АМ -точка L. Известно, что AD=AL=2 и ВЕ=1.
а) Постройте сечение пирамиды LAED плоскостью, проходящей через точку L и перпендикулярное ребру DE.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L.
Решение.
В пирамиде МАВС ребро МВ является высотой. Основание АВС – правильный треугольник со стороной 3.
По условию ребро АМ=5, AD=AL=2 и ВЕ=1. Тогда АЕ=АВ-ВЕ=3-1=2.
В прямоугольном треугольнике АВМ гипотенуза АМ=5, катет АВ=3, тогда катет МB=4 (египетский треугольник, т.е. треугольник со сторонами 3, 4 и 5).
а) Построим сечение пирамиды LAED плоскостью проходящей через точку L и перпендикулярное ребру DE.
Заметим, что основание этой этой пирамиды ADE-равносторонний треугольник со стороной 2. На самом деле: отрезок DE отсекает от каждой из сторон АС и АЕ отрезки по 2 см.
Следовательно, ∆ADE∾∆ACB по двум пропорциональным сторонам и углу между ними. Поэтому ∆ADE также является равносторонним со стороной 2.
Построение сечения: проведем LF⟘AB. Так как LF лежит в грани МАВ, перпендикулярной основанию АВС, то LF является высотой пирамиды LAED.
Из точки F опустим перпендикуляр FK на ребро DE, и точку К соединим с точкой L. По ТТП (теореме о трех перпендикулярах) LK⟘DE (LK-наклонная к плоскости ADE, KF-её проекция, DE-прямая на плоскости, проведенная через основание наклонной перпендикулярно её проекции).
Так как DE⟘ FK и DE⟘ LK, то DE перпендикулярно плоскости LFK.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Таким образом, LFK-сечение пирамиды LAED плоскостью, проходящей через точку L перпендикулярно DЕ.
б) Найдем площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L, т.е. площадь треугольника DEL, которая будет равна половине произведения стороны DE на высоту LK, проведенную к этой стороне.
Так как LK-гипотенуза в прямоугольном треугольнике LFK, то потребуется найти катеты LF и FK.
∆ ABM ∾ ∆ AFL, как прямоугольные треугольники, имеющие один общий острый угол А. Отсюда
Из прямоугольного ∆AFL по теореме Пифагора находим:
Мы уже установили, что треугольник ADE, подобный треугольнику АВС, является равносторонним. Все углы равностороннего треугольника равны 60°. Из прямоугольного треугольника EKF следует:
Искомая площадь сечения:
Радиус основания конуса с вершиной
Задача. Радиус основания конуса с вершиной Р равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1:3.
а) Постройте сечение конуса плоскостью, проходящей через точки А, В и Р.
б) Найдите площадь сечения конуса плоскостью АВР.
Решение.
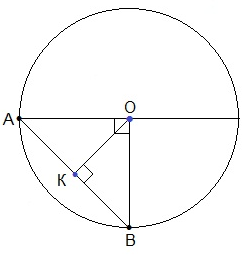а) Сечение конуса плоскостью, проходящей через точки А, В и Р – это равнобедренный ∆АРВ, основание которого сторона АВ – хорда окружности, стягивающая дугу 90°. А почему? На самом деле, так как по условию, точки А и В делят окружность на две дуги, отношение которых 1 : 3, то меньшая дуга будет равна одной четвёртой части от 360°- градусной меры всей окружности.
Далее, имеем треугольник АОВ — прямоугольный равнобедренный с катетом АО=6 (радиус основания конуса). Тогда
Проведем радиус, перпендикулярный хорде, который пересечет хорду в точке К.
ОК – медиана прямоугольного равнобедренного треугольника АОВ, поэтому,
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
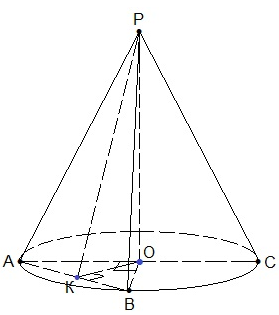б) Площадь сечения конуса плоскостью АВР -это площадь треугольника АВР, которую найдем как половину произведения его стороны АВ на высоту РК, проведенную к этой стороне.
где РК-медиана, а потому и высота равнобедренного треугольника АВР. Из прямоугольного треугольника АКР по теореме Пифагора:
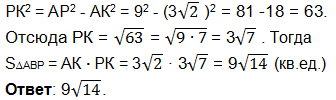
В правильной треугольной пирамиде МАВС с основанием АВС
Задача. В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ – точка L. Известно, что СD=ВE=LА=2.
а) Докажите, что отрезок DE содержит центр основания пирамиды.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
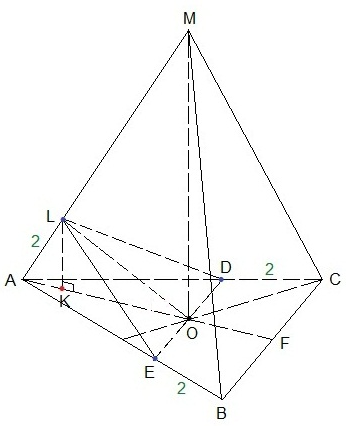а) В равностороннем треугольнике АВС, CD=BE=2 по условию, следовательно,
AD=AE=4. Треугольники ADE и ABC подобны по общему углу ВАС и соответственно пропорциональным сторонам этого угла:
Соответственные высоты этих подобных треугольников относятся друг к другу так же, т.е. АО : AF = 2 : 3.
Это означает, что точка О – середина отрезка DE, делит отрезок AF в отношении 2 : 1, считая от вершины. Следовательно, точка О является точкой пересечения медиан правильного треугольника АВС, т.е. центром основания пирамиды. Мы доказали, что отрезок DE содержит центр основания пирамиды.
б) Проведем отрезки LE и LD.
∆ DEL — сечение пирамиды плоскостью, проходящей через точки E, D и L. Требуется найти площадь этого сечения, т.е. площадь треугольника DEL. Проведем отрезок LO, этот отрезок является медианой, а, значит, и высотой равнобедренного треугольника DEL. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Проведем LK ⟘АО и получим прямоугольный ∆ LOK, из которого можно будет найти LO. Также потребуется найти DE.
Нам нужно найти и LK и OK.
Значение LK найдем из подобия прямоугольных треугольников АОМ и АКL.
Итак, нам лишь потребуется найти МО – высоту пирамиды, которая является катетом в прямоугольном треугольнике АОМ.
Найдем АО, как радиус окружности, описанной около правильного треугольника АВС, по формуле:
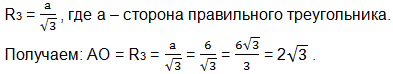
Из треугольника АОМ по теореме Пифагора:
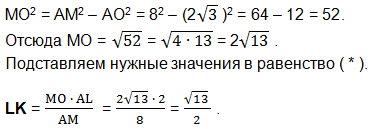
Значение ОК найдем как разность отрезков АО и АК.
Значение АК найдем также из подобия прямоугольных треугольников АОМ и АКL.
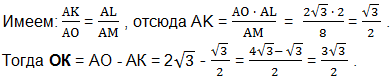
Из прямоугольного треугольника LOК по теореме Пифагора найдем LO.
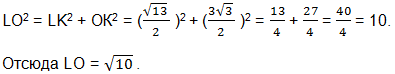
Осталось найти DE. Из подобия треугольников АВС и AED следует, что
