В правильной шестиугольной призме все рёбра равны 2
Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 2.
а) Постройте сечение призмы плоскостью, проходящей через точки В, А1 и F1.
б) Найдите расстояние от точки В до прямой А1F1.
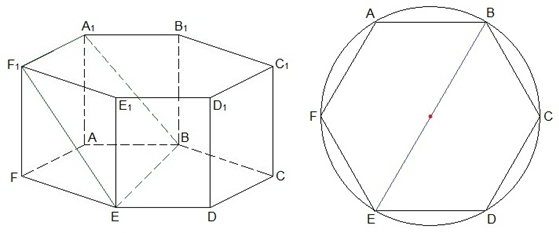
а) Верхнее основание плоскость BA1F1 пересекает по прямой A1F1. С нижним основанием секущая плоскость имеет общую точку В. Плоскость пересекает параллельные плоскости A1B1C1D1E1F1 и ABCDEF по параллельным прямым, следовательно, так как BE параллельна AF, то параллельна A1F1 и является прямой пересечения плоскости BA1F1 с нижним основанием призмы. Соединим A1 и B; F1 и E.
 Трапеция A1BEF1 – сечение призмы плоскостью, проходящей через точки B, A1 и F1.
Трапеция A1BEF1 – сечение призмы плоскостью, проходящей через точки B, A1 и F1.
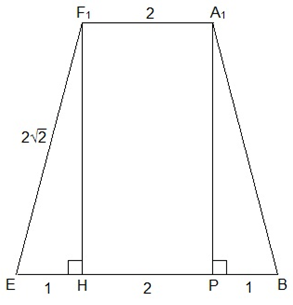
Так как A1B и EF1 – диагонали равных квадратов, то мы имеем равнобокую трапецию, в которой расстояние от B до A1F1 является расстоянием между основаниями трапеции, т.е. является высотой трапеции. Рассмотрим трапецию A1BEF1.
A1F1 = 2 (все ребра призмы по 2); BE = 4;
![]()
Это диагональ квадрата со стороной 2. Проведем F1H⟘BE – высоту трапеции. Отрезок ЕН=(4-2) : 2=1.
Из прямоугольного ∆ EHF1 по теореме Пифагора:
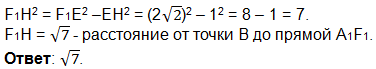
Навигация
Предыдущая статья: ← В правильной четырёхугольной пирамиде SABCD все рёбра равны 1
Следующая статья: Высота цилиндра равна 3, а радиус основания равен 13 →



Комментирование закрыто.