В правильной шестиугольной призме все рёбра равны 3
Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 3.
а) Постройте сечение призмы плоскостью, проходящей через точки D, А1 и B1.
б) Найдите расстояние от точки D до прямой А1B1.
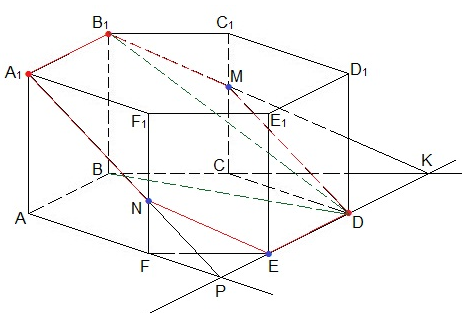
Решение. a) Сечение проходит через ребро A1B1 верхнего основания и точку D нижнего основания. Так как основания призмы параллельны, то линии пересечения их плоскостью DA1B1 также параллельны, т.е. плоскость DA1B1 пересечет нижнее основание по прямой DE, параллельной ребру А1В1. Найдем еще одну точку пересечения секущей плоскости с плоскостью грани ВВ1С1С. Для этого находим точку пересечения прямых ВС и DE. Получаем точку К. Следовательно, грань ВВ1С1С пересекается с секущей плоскостью в точках В1 и М, которая будет лежать на ребре СС1. У секущей плоскости имеются две общие точки с гранью СС1D1D — это точки M и D, поэтому прямая пересечения MD.
Аналогично, находим еще одну общую точку грани АА1F1F с секущей плоскостью. Для этого продолжаем AF и DE до пересечения в точке Р. Проводим A1P, которая пересечет ребро FF1 в точке N. Соединим точки N и E.
NE — это линия пересечения секущей плоскости с гранью FF1E1E.
Сечение представляет собой шестиугольник A1B1MDEN.
б) Расстояние от точки D до прямой A1B1 — это расстояние между параллельными сторонами шестиугольника A1B1MDEN – рёбрами А1В1 и DE. Проведем B1D и BD.
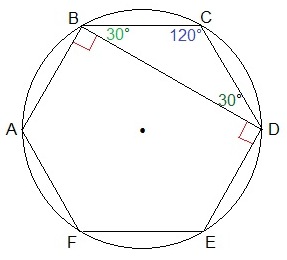 Так как малая диагональ BD правильного шестиугольника ABCDEF образует с его стороной DE прямой угол, то на основании ТТП (теоремы о трёх перпендикулярах)
Так как малая диагональ BD правильного шестиугольника ABCDEF образует с его стороной DE прямой угол, то на основании ТТП (теоремы о трёх перпендикулярах)
DE ⟘ B1D (B1D-наклонная, BD- её проекция, DE-прямая на плоскости, перпендикулярная проекции наклонной).
Это означает, что отрезок В1D и есть расстояние между параллельными рёбрами А1В1 и DE.
В прямоугольном треугольнике В1ВD гипотенузу В1D найдем по теореме Пифагора.
Нам известен катет ВВ1, а второй катет BD найдем по теореме косинусов из равнобедренного треугольника ВСD:
BD2 = BC2 + CD2-2 ∙ BC ∙ CD ∙ cos120°;
BD2 = 32 + 32 -2 ∙ 3 ∙ 3 ∙ (-cos60°);
BD2 = 9 + 9-2 ∙ 3 ∙ 3 ∙ (-0,5);
BD2 = 9 + 9 + 9 = 27.
Теперь из прямоугольного треугольника В1ВD по теореме Пифагора:
B1D2 = B1B2 + BD2 = 32 + 27 = 9+27 = 36. Отсюда В1D = 6.
Ответ: 6.
В правильной шестиугольной призме все рёбра равны 2
Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 2.
а) Постройте сечение призмы плоскостью, проходящей через точки В, А1 и F1.
б) Найдите расстояние от точки В до прямой А1F1.
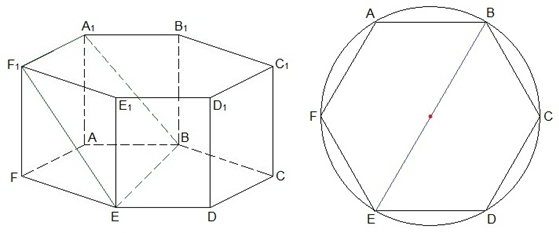
а) Верхнее основание плоскость BA1F1 пересекает по прямой A1F1. С нижним основанием секущая плоскость имеет общую точку В. Плоскость пересекает параллельные плоскости A1B1C1D1E1F1 и ABCDEF по параллельным прямым, следовательно, так как BE параллельна AF, то параллельна A1F1 и является прямой пересечения плоскости BA1F1 с нижним основанием призмы. Соединим A1 и B; F1 и E.
 Трапеция A1BEF1 – сечение призмы плоскостью, проходящей через точки B, A1 и F1.
Трапеция A1BEF1 – сечение призмы плоскостью, проходящей через точки B, A1 и F1.
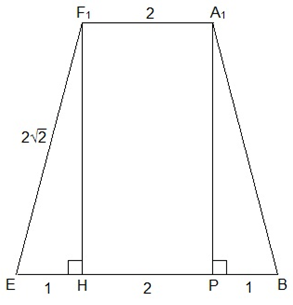
Так как A1B и EF1 – диагонали равных квадратов, то мы имеем равнобокую трапецию, в которой расстояние от B до A1F1 является расстоянием между основаниями трапеции, т.е. является высотой трапеции. Рассмотрим трапецию A1BEF1.
A1F1 = 2 (все ребра призмы по 2); BE = 4;
![]()
Это диагональ квадрата со стороной 2. Проведем F1H⟘BE – высоту трапеции. Отрезок ЕН=(4-2) : 2=1.
Из прямоугольного ∆ EHF1 по теореме Пифагора: