Найдите все значения а, при каждом из которых функция f(x) имеет хотя бы одну точку максимума
Задача. Найдите все значения а, при каждом из которых функция
f(x) = x2-4|x-a2|-8x
имеет хотя бы одну точку максимума.
Решение. Раскроем модульные скобки.
1) Пусть х-а2 ≥ 0, т.е. х ≥ a2. Получаем:
f(x) = x2-4x + 4a2-8x;
f(x) = x2-12x + 4a2. Вершина параболы А(m; n).
![]()
n = f(m) = f(6) = 62-12 ∙ 6 + 4a2 = 36-72 + 4a2 = 4a2-36.
A(6; 4a2-36). Ветви параболы f(x) = x2-12x + 4a2 направлены вверх, следовательно,
A(6; 4a2-36) – точка минимума функции.
2) Пусть х-а2 < 0, т.е. х < a2. Получаем:
f(x) = x2 + 4x-4a2-8x;
f(x) = x2-4x-4a2. Вершина параболы В(m; n).
![]()
n = f(m) = f(2) = 22-4 ∙ 2-4a2 = 4-8-4a2 = -4-4a2.
В(2; -4-4a2). Ветви параболы f(x) = x2-4x-4a2 направлены вверх, следовательно,
В(2; -4-4a2) – точка минимума функции.
Как могут быть расположены на оси Ох числа а2, 2 и 6, чтобы функция имела точку максимума?
Точка, соответствующая значению а2 должна лежать между точками, соответствующими числам 2 и 6. Тогда возрастание функции
f(x) = x2-4x-4a2 при 2 < x < a2 сменится убыванием функции
f(x) = x2-12x + 4a2 при a2 < x < 6, и точка пересечения парабол будет являться точкой максимума функции.
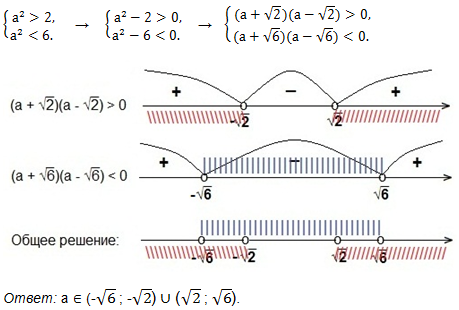
Итак, данная функция будет иметь точку максимума при условии, что 2 < a2 < 6. Значение а найдём из решения системы неравенств:
Задача. Найдите все значения а, при каждом из которых множество значений функции содержит отрезок [0; 1]
Задача. Найдите все значения а, при каждом из которых множество значений функции
![]()
Решение. Отрезок [0; 1] содержится в множестве значений данной функции тогда и только тогда, когда уравнения
![]()
имеют решения. Решаем каждое из этих уравнений.
![]()
Знаменатель этой дроби можно записать в виде:
(10х+а)2+15. Это выражение при любых а и х положительно, поэтому данная дробь будет равна нулю, если числитель дроби будет равен нулю.
5а+150х-10ах=0 → а+30х-2ах=0 → 2х(а-15)=а. Это уравнение имеет решение при любом а ≠ 15.
![]()
Умножим обе части равенства на знаменатель дроби.
5а+150х-10ах=100х2+20ах+а2+25. Упростим это выражение.
100х2+20ах+а2+25-5а-150х+10ах=0 → 100х2+30ах-150х+а2-5а+25=0;
100х2+2(15а-75)х+а2-5а+25=0. Это уравнение имеет решение тогда и только тогда, когда его дискриминант неотрицателен.
![]()
D1 = 225a2-2250a+5625-100a2+500a-2500=125a2-1750a+3125=125(a2-14a+25)≥0. Решим уравнение a2-14a+25=0. Дискриминант этого уравнения
D’=72-25=49-25=24.
Тогда корни уравнения
![]()
Решениями неравенства (a2-14a+25)≥0
служит множество значений переменной а, удовлетворяющих условию
![]()
Исключаем из этих промежутков значение а ≠ 15.
![]()
Найдите все значения а, при каждом из которых функция
Задача. Найдите все значения а, при каждом из которых функция
f(x) = x2-3|x-a2|-5x
имеет более двух точек экстремума.
Решение. Экстремум (минимум или максимум) функции возможен в точке, в которой производная функции меняет знак. Раскроем модульные скобки.
1) Случай. Пусть х-а2 ≥ 0 → х ≥ а2. Получаем f(x) = x2-3x + 3a2-5x;
f(x) = x2-8x + 3a2. Находим производную. f ’(x) = 2x-8 = 2(x-4). Критическая точка х = 4. Производная в точке х = 4 меняет знак с «-» на «+». Следовательно, в точке х = 4 функция f(x) = x2-8x + 3a2 имеет минимум.
 Найдём значение функции в точке х = 4.
Найдём значение функции в точке х = 4.
f(4) = 42-8 ∙ 4 + 3a2 = 3a2-16.
Итак, xmin = 4; fmin = 3a2-16.
2) Случай. Пусть х-а2 < 0 → х < а2. Получаем f(x) = x2 + 3x-3a2-5x;
f(x) = x2-2x-3a2. Находим производную.
f ’(x) = 2x-2 = 2(x-1). Критическая точка х = 1. Производная в точке х = 1 меняет знак с «-» на «+». Следовательно, в точке
х = 1 функция f(x) = x2-2x-3a2 имеет минимум.
Найдём значение функции в точке х = 1.
f(1) = 12-2 ∙ 1-3a2 = -1-3a2.
Итак, xmin = 1; fmin = -1-3a2.
Чтобы изобразить функции графически в каждом из двух рассмотренных случаев нам нужно определиться со значением числа а2.
Возможны три варианта расположения числа а2.
Вариант 1.
а2 < 1 < 4. Для определённости возьмём а2 = 0.
Функция f(x) = x2-8x + 3a2 имеет xmin = 4; fmin = 3a2-16 = -16.
Строим параболу f(x) = x2-8x + 3a2, вершина которой A(4; -16).
Так как функцию f(x) = x2-8x + 3a2 мы получили при условии,
что х ≥ а2, то надо взять точки параболы, удовлетворяющие условию х ≥ 0.
 Функция f(x) = x2-2x-3a2 имеет
Функция f(x) = x2-2x-3a2 имеет
xmin = 1; fmin = -1-3a2= -1.
Строим параболу f(x) = x2-2x-3a2 с вершиной В(1; -1).
Так как функцию f(x) = x2-2x-3a2 мы получили при условии, что х < а2, то надо взять точки параболы, удовлетворяющие условию х < 0.
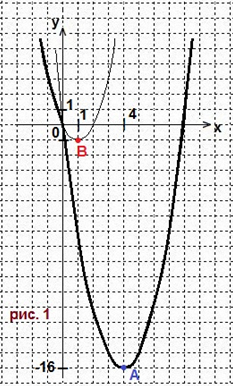
Смотрите рис.1. Получается только 1 экстремум.
Вывод: вариант 1 не подойдёт.
Вариант 2.
1 < а2 < 4. Для определённости возьмём а2 = 3.
Функция f(x) = x2-8x + 3a2 имеет xmin = 4; fmin = 3a2-16 = 3 ∙ 3-16 = -7.
Строим параболу f(x) = x2-8x + 3a2, вершина которой A(4; -7).
Так как функцию f(x) = x2-8x + 3a2 мы получили при условии,
что х ≥ а2, то надо взять точки параболы, удовлетворяющие условию х ≥ 3.
Функция f(x) = x2-2x-3a2 имеет xmin = 1; fmin = -1-3a2= -1-3 ∙ 3 = -10.
Строим параболу f(x) = x2-2x-3a2 с вершиной В(1; -10).
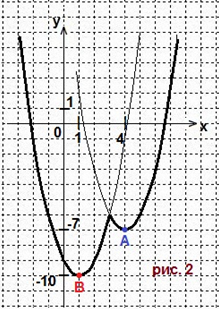
Так как функцию f(x) = x2-2x-3a2 мы получили при условии, что х < а2, то надо взять точки параболы, удовлетворяющие условию х < 3. Смотрите рис.2. Получается 3 экстремума.
Вывод: вариант 2 (1 < а2 < 4 ) подходит. Найдём значение а, решив систему неравенств:
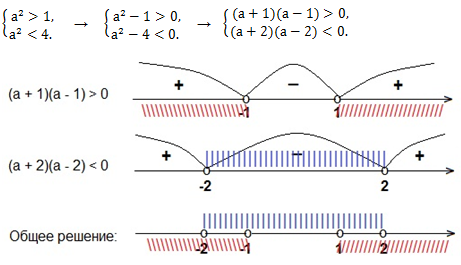
 Получаем а (-2; -1) (1; 2).
Получаем а (-2; -1) (1; 2).
Вариант 3.
1 < 4 < а2.
Для определённости возьмём а2 = 5.
Функция f(x) = x2-8x + 3a2 имеет
xmin = 4; fmin = 3a2-16 = 3 ∙ 5-16 = -1.
Строим параболу f(x) = x2-8x + 3a2, вершина которой A(4; -1).
Так как функцию f(x) = x2-8x + 3a2 мы получили при условии, что х ≥ а2, то надо взять точки параболы, удовлетворяющие условию х ≥ 5.
Функция f(x) = x2-2x-3a2 имеет
xmin = 1; fmin = -1-3a2= -1-3 ∙ 5 = -16.
Строим параболу f(x) = x2-2x-3a2 с вершиной В(1; -16).
Так как функцию f(x) = x2-2x-3a2 мы получили при условии, что х < а2, то надо взять точки параболы, удовлетворяющие условию х < 5.
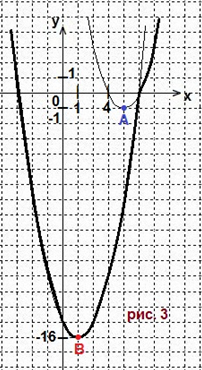
Смотрите рис.3. Получается только 1 экстремум. Вывод: вариант 3 не подойдёт.
Ответ: а (-2; -1) (1; 2).
Найдите все значения а, при каждом из которых система уравнений
Задача. Найдите все значения а, при каждом из которых система уравнений
![]()
имеет более одного решения.
Решение. Рассмотрим первое уравнение системы.
1) Пусть х2 + у2 -25 ≥ 0. Неравенство х2 + у2 ≥ 25 или х2 + у2 ≥ 52 описывает множество точек координатной плоскости, лежащих вне круга с центром в начале координат и радиусом R = 5. На чертеже круг показан зелёным цветом.
Раскроем модульные скобки.
х2 + 20х + у2 -20у + 75 = х2 + у2-25;
20x-20y + 100 = 0. Разделим обе части равенства на 20.
х-у + 5 = 0; у = х + 5. Графиком служит прямая у = х, смещённая вдоль оси Оу на 5 единичных отрезков. Нам подойдут только те точки прямой у = х + 5, которые будут лежать вне круга х2 + у2 = 25. На чертеже показана эта часть прямой синим цветом.

2) Пусть х2 + у2-25 ≤ 0. Неравенство х2 + у2 ≤ 25 или х2 + у2 ≤ 52 описывает множество точек координатной плоскости, лежащих внутри круга с центром в начале координат и радиусом R = 5.
Раскроем модульные скобки.
х2 + 20х + у2 -20у + 75 = -х2 -у2 + 25;
2х2 + 20х + 2у2 -20у + 50 = 0. Разделим обе части равенства на 2.
х2 + 10х + у2 -10у + 25 = 0. Преобразуем это выражение.
x2 + 2 ∙ х ∙ 5 + 52-52 + y2 -2 ∙ y ∙ 5 + 52-52 + 25 = 0;
(x2 + 2 ∙ х ∙ 5 + 52) + (y2 -2 ∙ y ∙ 5 + 52) = 25;
(х + 5)2 + (у-5)2 = 52.
Это уравнение описывает окружность с центром в точке (-5; 5) и радиусом R = 5. Нам подойдут только те точки этой окружности, которые будут лежать внутри окружности
х2 + у2 = 25. На чертеже эти точки окружности обозначены красным цветом.
Рассмотрим второе уравнение системы.
х-у = а. Запишем равенство в виде: у = х-а. Графиком этой функции будет служить прямая у = х, смещённая вдоль оси Оу на а единичных отрезков. Для того, чтобы система уравнений имела более одного решения прямая у = х-а должна пересечь сине-красную линию чертежа два и более раз.
Решим систему уравнений у = х-а и х2 + 10х + у2 -10у + 25 = 0.
Подставим значение у = х-а в выражение х2 + 10х + у2 -10у + 25 = 0. Получаем:
х2 + 10х + (х-а)2 -10(х-а) + 25 = 0. Раскроем скобки.
х2 + 10х + х2-2ах + а2-10х +10а + 25 = 0;
2х2 -2ах + а2 +10а + 25 = 0.
Дискриминант D1 = a2-2(а2 +10а + 25) = a2-2а2-20а-50 = -а2-20а-50. Если дискриминант больше нуля, то последнее уравнение, а значит, и вся система имеют два действительных корня.
D1 > 0 → -а2-20а-50 > 0 → а2 + 20а + 50 < 0.
Это неравенство будет верным при a1 < a < a2, где a1 и a2 — корни квадратного уравнения а2 + 20а + 50 = 0.
Решим уравнение а2 + 20а + 50 = 0.
D1 = 102-50 = 50.
![]()
Таким образом, а2 + 20а + 50 < 0

и не будет иметь общих точек с графиком первого уравнения данной системы (с сине-красной линией).

и будет касаться красной линии. В точке касания система будет иметь единственное решение. Очевидно, что если мы будем перемещать прямую
![]()
параллельно самой себе в направлении прямой у = х + 5, то каждый раз будем получать по две точки пересечения, и данная система будет иметь два решения.
![]()
совпадет с прямой у = х + 5, то это будет означать, что данная система имеет множество решений.
Если бы вторым уравнением данной системы было уравнение, приводящееся к виду
у = х + а, то мы бы сказали, что данная система будет иметь более двух решений
![]()
У нас же прямая у = х-а или у = х + (- а), следовательно, при условии:
![]()
прямая у = х + (- а) пересечёт сине-красную линию более двух раз и, значит, данная система будет иметь более одного решения.
![]()


