Проценты и кредиты ЕГЭ 2022. Часть 4
ЕГЭ 2022 ФИПИ. Вариант 3. Задача 15.
По вкладу «А» банк в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 12 % в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
Решение.
Обозначим искомое число процентов через r.
Оформим рассуждения по условию задачи в виде таблицы.

Так как вклад «Б» будет менее выгоден, чем вклад «А», то справедливо неравенство:
1,122 ∙S + 1,122 ∙S ∙0,01r < 1,23 ∙S.
Разделим обе части неравенства на S.
1,122 ∙0,01r < 1,23 -1,122;
1,2544 ∙0,01r < 1,728 -1,2544;
1,2544 ∙0,01r < 0,4736;
1,2544r < 47,36;
r < 47,36 : 1,2544;
r < 37,75…
r = 37 – наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
Ответ: 37.
Экономические задачи ЕГЭ Это страница с нужной вам задачей
ЕГЭ 2022 ФИПИ. Вариант 4. Задача 15.
По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Решение.
Обозначим искомое число процентов через r.
Оформим рассуждения по условию задачи в виде таблицы.

Так как вклад «Б» будет менее выгоден, чем вклад «А», то справедливо неравенство:
1,142 ∙S + 1,142 ∙S ∙0,01r > 1,13 ∙S.
Разделим обе части неравенства на S.
1,142 ∙0,01r > 1,13 -1,142;
1,2996 ∙0,01r > 1,331 -1,2996;
1,2996 ∙0,01r > 0,0304;
1,2996 > 3,04;
r > 3,04 : 1,2996;
r > 2,33…
r = 3 – наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Ответ: 3.
ЕГЭ 2022 ФИПИ. Вариант 17. Задача 15.
Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Решение.
1-й месяц. Александр не смог купить акции за 100 тысяч рублей. Он отложил Х тысяч рублей
2-й месяц. Акции стоят 1,3 ∙100 тыс. рублей. Александр отложил Хтыс. рублей.
3-й месяц. Акции стоят 1,32 ∙100 тыс. рублей. Александр отложил Х тыс. рублей.
4-й месяц. Акции стоят 1,33 ∙100 тыс. рублей. Александр отложил Хтыс. рублей.
…………………………………………………………………………………………………
n-й месяц. Акции стоят 1,3n-1 ∙100 тыс. рублей. Александр отложил Х тыс. рублей.
Итак, за n месяцев Александр отложил nХ тысяч рублей, и наконец, может купить акции, т.е.

Нужно найти минимальное целое значение n, при котором производная будет менять знак с минуса на плюс. Это значение n и будет точкой минимума функции
Производная отрицательна при n ∙ ln1,3 -1 < 0. Решаем неравенство:
ln1,3n < 1;
ln1,3n < lne;
1,3n < e. Помним, что е ≈ 2,72…
Так как n – количество месяцев, то будем подбирать целое значение показателя степени так, чтобы знак неравенства поменялся.
Если n = 2, то 1,32 = 1,69 < e;
Если n = 3, то 1,33 = 2,197 < e;
Если n = 4, то 1,34 = 2,8561 > e.
Таким образом, производная X’(n) поменяет знак с минуса на плюс на промежутке, содержащем n = 4. Это наименьшее целое значение n, при котором функция

Это означает, что Александру достаточно было откладывать по 54925 рублей в течение четырёх месяцев, чтобы купить пакет акций быстрорастущей компании.
Ответ: 54925 рублей.
ЕГЭ 2022 ФИПИ. Вариант 18. Задача 15.
Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Решение.
1-й месяц. Сергей не смог купить акции за 160 тысяч рублей. Он отложил Х тысяч рублей
2-й месяц. Акции стоят 1,25 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
3-й месяц. Акции стоят 1,252 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
4-й месяц. Акции стоят 1,253 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
…………………………………………………………………………………………………
n-й месяц. Акции стоят 1,25n-1 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
Итак, за n месяцев Александр отложил nХ тысяч рублей, и наконец, может купить акции, т.е.

Нужно найти минимальное целое значение n, при котором производная будет менять знак с минуса на плюс. Это значение n и будет точкой минимума функции
Производная отрицательна при n ∙ ln1,25 -1 < 0. Решаем неравенство:
ln1,25n < 1;
ln1,25n < lne;
1,25n < e. Помним, что е ≈ 2,72…
Так как n – количество месяцев, то будем подбирать целое значение показателя степени так, чтобы знак неравенства поменялся.
Если n = 2, то 1,252 = 1,5625 < e;
Если n = 3, то 1,253 ≈ 1,953 < e;
Если n = 4, то 1,254 ≈ 2,4 < e;
Если n = 5, то 1,255 ≈ 3,05 > e.
Таким образом, производная X’(n) поменяет знак с минуса на плюс на промежутке, содержащем n = 5. Это наименьшее целое значение n, при котором функция

Это означает, что Сергею достаточно было откладывать по 78125 рублей в течение пяти месяцев, чтобы купить пакет акций быстрорастущей компании.
Ответ: 78125 рублей.
ЕГЭ 2022 ФИПИ. Вариант 19. Задача 15.
Цена ценной бумаги на конец года вычисляется по формуле
S=1,1So + 2000, где So – цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12 %. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тыс. рублей, которые он может положить на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.
Решение.
По условию у Максима 80 тыс. рублей, которые он может или положить на счёт или купить ценную бумагу, т.е. So = 80 тыс. рублей.
Если в начале 2021 года Максим положит деньги на банковский счёт, то на конец года у него будет 1,12 So.
Запишем эту сумму в виде: 1,1So + 0,02So и сравним её с ценой ценной бумаги на конец года: 1,1So + 2000.
Так как 0,02So = 0,02 ∙ 80000 = 1600 < 2000, то выгоднее купить ценную бумагу.
Итак, если в начале 2021 года Максим купит ценную бумагу, то на конец года у него будет 1,1 ∙ 80000 + 2000 = 90000 рублей. Оставить ценную бумагу или продать?
Проверим значение 0,02So = 0,02 ∙ 90000 = 1800 < 2000. Значит, продавать ценную бумагу рано.
На конец 2022 года у Максима будет
1,1 ∙ 90000 + 2000 = 101000 рублей.
Оцениваем значение 0,02So = 0,02 ∙ 101000 = 2020 > 2000.
Следовательно, в начале 2023 года Максиму выгоднее продать ценную бумагу и положить деньги на банковский счёт.
На конец 2023 года у него может быть 1,12So = 1,12 ∙ 101000 = 113120 рублей.
На конец 2024 года у Максима может быть 1,12So = 1,12 ∙ 113120 = 126694,4 рублей.
Ответ: 126694,4 рублей.
ЕГЭ 2022 ФИПИ. Вариант 33. Задача 15.
15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы:
— 11-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 15-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.
Решение.
За 15 месяцев банку заплатили 1300-100=1200 тысяч рублей основного долга,
что составляет 1200 : 15 = 80 тысяч рублей – сумму, на которую ежемесячно уменьшается долг.
Однако, r % ежемесячно нужно выплачивать с суммы остатка долга, начиная с выданной суммы кредита 1300 тысяч рублей, а затем с суммы за вычетом 80 тысяч рублей ежемесячно. Проценты считаются так:
1 месяц. 1300 ∙ 0,01r = 13r;
2 месяц (1300-80) ∙ 0,01r = 1220 ∙ 0,01r = 12,2r;
3 месяц (1220-80) ∙ 0,01r =1140 ∙ 0,01r = 11,4r;
4 месяц (1140-80) ∙ 0,01r =1060 ∙ 0,01r = 10,6r и так далее.
Заметим, что последовательность чисел 13r; 12,2r; 11,4r; 10,6r и т.д. представляет собой арифметическую прогрессию с первым членом
а1 = 13r и разностью d=-0,8r. Нам нужно найти сумму 15-ти членов этой арифметической прогрессии. Воспользуемся формулой:

Итак, банку придётся отдать 1200 тысяч рублей плюс 111r тысяч рублей процентов за первые 15 месяцев и ещё за 16-й месяц долг 100 тысяч рублей плюс проценты с этой суммы, т.е. r % от 100 тысяч (это 0,01r ∙ 100 = r). Общая сумма выплат по условию равна 1636 тысяч рублей. Получим равенство:
1200+111r+100+r = 1636;
112r = 336;
r = 3.
Ответ: 3%.
ЕГЭ 2022 ФИПИ. Вариант 34. Задача 15.
15 мая планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 16-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 17-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1472 тысячи рублей?
Решение.
Обозначим через Х сумму, которую нужно будет выплатить банку к 15-му числу 17-го месяца в счёт основного долга.
За 16 месяцев банку заплатят 16 ∙ 50 = 800 тысяч рублей основного долга.
Значит, 1472-800=672 тысячи рублей – это проценты за 16 месяцев,
а также за 17-й месяц сумма Х с процентами, т.е. Х+0,02Х=1,02Х.
Итак, взятая сумма кредита (800+Х) тысяч рублей, и нам надо подсчитать проценты с этой суммы за первые 16 месяцев кредитования.
Рассуждаем: в первый месяц банк начислит 2 % на сумму (800+Х), во второй месяц 2 % на сумму (750+Х), затем на (700+Х), на (650+х) и т.д. А в 16-й месяц кредитования банк начислит 2 % на сумму (50+Х) тысяч рублей.
Таким образом, нам надо найти значение выражения:
0,02 ∙ ((800+Х)+(750+Х)+(700+Х)+…+(50+Х)).
Сумма в скобках – это сумма арифметической прогрессии с первым членом

Это проценты за первые 16 месяцев кредитования.
Итак, получим равенство:
1,02Х+136+0,32Х= 672;
1,34Х=672-136;
1,34Х=536;
Х=400.
За 17 месяц в счёт основного долга нужно выплатить 400 тысяч рублей. Тогда в кредит планируется взять 800+400=1200 тысяч рублей.
Ответ: 1 200 000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 36. Задача 15.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
I способ решения. Если кредит на S рублей полностью погашается за n ежегодных выплат, равных X1, X2, X3, …, Xn, осуществленных после начисления r% по вкладу, то применяем формулу:

Кредит Михаила S полностью погашается за 4 платежа по 2928200 рублей каждый, после начисления r = 10% годовых каждый год на оставшуюся сумму долга. Таким образом, так как X1=X2=X3=X4=2928200, получаем сумму взятого кредита:

Окончательно S = 2000000 ∙ 4,641 = 9282000 рублей.
Ответ: 9282000.
II способ решения (традиционный).
Пусть Михаил взял в банке S рублей.
1) Банк начислил на эту сумму 10% и долг составил 1,1S рублей. Михаил выплатил 2928200 рублей. Долг составил (1,1S-2928200) рублей.
2) Банк начислил 10% и долг составил 1,1(1,1S-2928200) рублей. Михаил выплатил 2928200 рублей. Долг составил (1,1(1,1S-2928200)-2928200) рублей.
3) Банк начислил 10% и долг составил 1,1(1,1(1,1S-2928200)-2928200) рублей. Михаил выплатил 2928200 рублей.
Долг составил (1,1(1,1(1,1S-2928200)-2928200)-2928200) рублей.
4) Банк начислил 10% и долг составил
1,1(1,1(1,1(1,1S-2928200)-2928200)-2928200). Банк выплатил 2928200 рублей, и долг был полностью погашен. Составим равенство:
1,1(1,1(1,1(1,1S-2928200)-2928200)-2928200)-2928200=0;
1,14⋅ S-1,13⋅2928200-1,12⋅2928200-1,1⋅2928200-2928200=0;
1,4641S-1,331⋅2928200-1,21⋅2928200-1,1⋅2928200-2928200=0;
1,4641S-4,641⋅2928200=0;
1,4641S=4,641⋅2928200;
S=4,641⋅2000000;
S=9 282000.
Ответ: 9 282 000.
Примечание. Если обозначить 2 928 200 рублей через Х, то записи решения были бы короче.
Смотрите сами.
Итак, обозначим каждый из четырёх ежегодных платежей через Х.
Пусть Х=2928200 рублей, а взял Михаил в банке S рублей.
1) Банк начислил на эту сумму 10% и долг составил 1,1S. Михаил выплатил Х рублей. Долг составил 1,1S-Х.
2) Банк начислил 10% и долг составил 1,1(1,1S-Х)=1,12 ∙ S-1,1X. Михаил выплатил X. Долг составил 1,12 ∙ S-1,1X-X.
3) Банк начислил 10% и долг составил 1,1(1,12∙S-1,1X-X)=1,13∙S-1,12X-1,1X. Михаил выплатил X рублей.
Долг составил 1,13∙S-1,12X-1,1X-X.
4) Банк начислил 10% и долг составил
1,1(1,13∙S-1,12X-1,1X-X)=1,14∙S-1,13X-1,12 X-1,1X.
Банк выплатил X, и долг был полностью погашен. Получаем равенство:
1,14∙S-1,13X-1,12 X-1,1X-Х=0.
1,14∙S=1,13X+1,12 X+1,1X+Х=0;
1,4641S=1,331X+1,21X+1,1X+X;
1,4641S=4,641X;
S=4,641X :1,4641. Так как Х=2928200, то
S=4,641∙2928200 :1,4641;
S=4,641⋅2000000;
S=9 282 000.
Ответ: 9 282 000.
Ниже простые и очень полезные формулы:
k2 ⋅ S = (k +1) ⋅ Х . ( I**)
k 3 ⋅ S = (k2 + k + 1) ⋅ Х. ( II**)
k 4 ⋅ S = (k3 + k2 + k + 1) ⋅ Х. ( III**)
Здесь: S – сумма кредита, выданная банком под r%, которая полностью погашается платежами по Х рублей каждый. Значение k=1+0,01r. Показатель степени с основанием k – это количество платежей по Х рублей.
В рассмотренной задаче мы рассуждениями получили формулу ( III**).
Решить логарифмическое неравенство
Решите неравенство lg4(x2 – 26)4 – 4lg2(x2 – 26)2 ≤ 240.

Применим формулу для логарифма степени и запишем
lg(x2 – 26)4 как 2lg(x2 – 26)2. А почему не как 4lg(x2 – 26)? Потому что в этом случае число под знаком логарифма должно быть положительным, а не просто не равным нулю, как мы записали в ОДЗ. Это значит, что преобразованное далее неравенство не будет равносильно данному. Итак:
lg4(x2 – 26)4 = (lg(x2 – 26)4 )4 = (2lg(x2 – 26)2 )4 = 24 · (lg(x2 – 26)2 )4 = 16lg4(x2 – 26)2.
Тогда данное неравенство примет вид:
16lg4(x2 – 26)2 – 4lg2(x2 – 26)2 ≤ 240. Делим обе части на 4.
4lg4(x2 – 26)2 – lg2(x2 – 26)2 – 60 ≤ 0.
Сделаем замену. Пусть lg2(x2 – 26)2 = t.
Решим неравенство. 4t2 – t – 60 ≤ 0.
Находим корни квадратного трёхчлена.
4t2 – t – 60 = 0. D = b2 – 4ac = 1 + 960 = 961 = 312.

0 ≤ lg2(x2 – 26)2 ≤ 4.
lg2(x2 – 26)2 ≤ 4. Извлекаем из обеих частей квадратные корни.
| lg(x2 – 26)2| ≤ 2.
-2 ≤ lg(x2 – 26)2 ≤ 2. (см. рис. 2)

Запишем числа -2 и 2 в виде десятичного логарифма.
lg0,01 ≤ lg(x2 – 26)2 ≤ lg100. Логарифмическая функция с основанием 10 является возрастающей, поэтому последнее неравенство равносильно неравенству
0,01 ≤ (x2 – 26)2 ≤ 100. А это неравенство равносильно системе неравенств
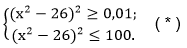
Решаем каждое неравенство системы по отдельности, а затем находим их общее решение. Оно и будет служить решением данного неравенства.

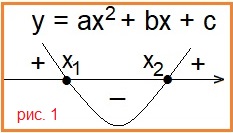
I. (x2 – 26)2 ≥ 0,01; (см. рис.3)
| x2 – 26| ≥ 0,1;
1) x2 – 26 ≤ -0,1
x2 ≤ 25,9.

2) x2 – 26 ≥ 0,1
x2 ≥ 26,1.
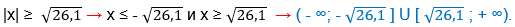
Решаем второе неравенство системы ( * )
II. (x2 – 26)2 ≤ 100;
| x2 – 26| ≤ 10;
-10 ≤ x2 – 26 ≤ 10
16 ≤ x2 ≤ 36;

Полученные решения неравенств I и II покажем синим и зелёным цветом на координатной прямой. Пересечение этих промежутков и будет решением нашего неравенства.




