В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы: каждый январь долг увеличивается на 10%
Задача. В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:
-каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
-с февраля по июнь необходимо выплатить одним платежом часть долга;
-в июле 2026, 2027, 2028, 2029 и 2030 долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
-в июле 2030 года долг должен составлять 800 тысяч рублей;
-в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же сумму меньше долга на июль предыдущего года;
Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.
Решение. Пусть в каждый из первых пяти лет долг будет уменьшаться на х тыс. рублей. Так как через эти 5 лет долг должен составлять 800 тыс. рублей, то первоначальный кредит равен (5х+800). С этой суммы посчитаем все проценты, которые будут начислены банком в первые 5 лет:
0,1(5х+800 + 4х+800 + 3х+800 + 2х+800 + х+800) =
= 0,1 ∙ 15х + 0,1 ∙ 800 ∙ 5 = 1,5х + 400 (тыс. руб.).
С июля 2030 года долг должен составлять 800 тысяч рублей по условию. Погашать его нужно будет следующие 5 лет на одну и ту же сумму. Мы легко определим эту сумму. Делим 800 на 5 и получаем 160 тысяч рублей. Однако, для удобства подсчёта процентов за последние 5 лет, обозначим эту сумму через у. Итак,
у=160, значит, долг 800=5у. Считаем проценты:
0,1(5у+4у+3у+2у+у) = 0,1 ∙ 15у = 1,5у.
Заменяем у на 160 и получаем 1,5 ∙ 160 = 240 тысяч рублей – проценты за последние 5 лет.
Таким образом, за всё время кредитования клиент выплатит:
(5х + 800) тыс. руб. — данную банком сумму;
(1,5х + 400) тыс. руб. — проценты за первые 5 лет;
240 тыс. руб. — проценты за последние 5 лет.
По условию сумма выплат по кредиту равна 2090 тысяч рублей. Получаем уравнение:
5х + 800 + 1,5х + 400 + 240 = 2090. Решаем:
6,5х = 2090-1440;
6,5х = 650;
х = 100.
На 100 тыс. руб. будет уменьшаться долг ежегодно в первые 5 лет.
А так как взятую сумму кредита мы обозначали через (5х+800) тысяч рублей, то она составит 5 ∙ 100 + 800 = 1300 тысяч рублей.
Ответ: 1300000 рублей.
15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы: 1-го числа каждого месяца долг возрастает на 3%
Задача. 15-го декабря планируется взять кредит в банке на 11 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1198 тысяч рублей?
Решение. Для удобства обозначим через х величину, на которую ежемесячно уменьшался долг первые 10 месяцев (х = 80 тыс. рублей), а через у – остаток долга на 11 месяц кредитования (долг 15 числа 10-го месяца). Тогда, очевидно, что кредит был равен (10х + у) тысяч рублей.
Подсчитаем проценты за первые 10 месяцев.
0,03 ∙ ( (10х+у) + (9х+у) + (8х+у) + … + (х+у)) =
= 0,03 ∙ (10х + 9х + 8х +…+ х) + 0,03 ∙ 10у =
= 0,03 ∙ 55х + 0,3у = 1,65х + 0,3у.
За 11-й месяц будет выплачено (у + 0,03у) тыс. рублей.
Итак, за всё время кредитования клиент заплатил
10х + 1,65х + 0,3у + у + 0,03у или 1198 тыс. рублей.
10х – это 80 ∙ 10 = 800 тысяч рублей.
800 + 1,65х + 1,33у = 1198;
1,65 ∙ 80 + 1,33у = 1198-800;
132 + 1,33у = 398;
1,33у = 398-132;
1,33у = 266;
у = 200.
Ответ: 200 тысяч рублей.
В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей
Задача. В июле 2027 года планируется взять кредит на 10 лет в размере 1500 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 15% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2033, 2034, 2035, 2036 и 2037 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2037 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2400 тыс. рублей. Сколько рублей составит платёж в 2029 году?
Решение.
Условие «-в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
15% банк насчитывает на остаток долга.
0,15 ∙ (1500 + (1500-х) + (1500-2х) + (1500-3х) + (1500-4х)) =
= 0,15 ∙ (5 ∙ 1500 -10х) = 0,15(7500-10х) = (1125-1,5х) тыс. рублей.
Итак, к концу 2032 года (после 5 лет ежегодных выплат) долг составит (1500-5х) тыс. рублей или 5(300-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (300-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,15 ∙ (5(300-х) + 4(300-х) + 3(300-х) + 2(300-х) + (300-х)) =
= 0,15 ∙ 15(300-х) = 2,25 ∙ (300-х) = (675-2,25х) тыс. рублей.
По условию общая сумма выплат 2400 тыс. рублей, значит, сумма выплаченных процентов составит 2400-1500 = 900 тыс. рублей. Составим уравнение.
1125-1,5х + 675-2,25х = 900;
-1,5х-2,25х = 900-1125-675;
-3,75х = -900 | : (-3,75);
х = 240. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 240 тыс. рублей.
Искомый платёж за 2029 год составит эти 240 тыс. рублей плюс 15% от остатка долга, т.е. от суммы 1500-240 = 1260 тыс. рублей, так как в 2028 году уже было погашено 240 тыс. рублей.
Считаем: 240 + 0,15 ∙ 1260 = 240 + 189 = 429 тыс. рублей.
Ответ: 429000 рублей.
Задача. В июле 2026 года планируется взять кредит на 10 лет в размере 1300 тыс. рублей. Условия его возврата таковы:
-каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
-в июле 2032, 2033, 2034, 2035 и 2036 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
-к июлю 2036 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2780 тыс. рублей. Сколько рублей составит платёж в 2027 году?
Решение.
Условие «-в июле 2027, 2028, 2029, 2030 и 2031 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;» означает, что банк в первые 5 лет будет ежегодно погашать долг клиенту на одну и ту же сумму. Мы обозначим эту сумму через х. Это ежегодный платёж (в первые 5 лет) без процентов. Посчитаем проценты за первые 5 лет.
20% банк насчитывает на остаток долга.
0,2 ∙ (1300 + (1300-х) + (1300-2х) + (1300-3х) + (1300-4х)) =
= 0,2 ∙ (5 ∙ 1300 -10х) = 0,2(6500-10х) = (1300-2х) тыс. рублей.
Итак, к концу 2031 года (после 5 лет ежегодных выплат) долг составит (1300-5х) тыс. рублей или 5(260-х) тыс. рублей. Так как клиенту остаётся платить 5 лет – банк ежегодно будет засчитывать в счёт погашения долга пятую часть оставшейся суммы, т.е. (260-х) тыс. рублей, не забывая начислять проценты перед этим. Считаем проценты за вторые 5 лет кредитования.
0,2 ∙ (5(260-х) + 4(260-х) + 3(260-х) + 2(260-х) + (260-х)) =
= 0,2 ∙ 15(260-х) = 3 ∙ (260-х) = (780-3х) тыс. рублей.
По условию общая сумма выплат 2780 тыс. рублей, значит, сумма выплаченных процентов составит 2780-1300 = 1480 тыс. рублей. Составим уравнение.
1300-2х + 780-3х = 1480;
-2х-3х = 1480-1300-780;
-5х = -600 | : (-5);
х = 120. Следовательно, ежегодно в первые 5 лет банк будет засчитывать клиенту в счёт погашения долга по 120 тыс. рублей.
Искомый платёж за 2027 год составит эти 120 тыс. рублей плюс 20% от взятой суммы кредита в 1300 тыс. рублей, так как в 2027 году состоится самая первая выплата банку.
Считаем: 120 + 0,2 ∙ 1300 = 120 + 260 = 380 тыс. рублей.
Ответ: 380000 рублей.
15 января планируется взять кредит в банке на 25 месяцев
Задача. 15 января планируется взять кредит в банке на 25 месяцев. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 13% больше, чем сумма, взятая в кредит. Найдите r%.
Решение. Пусть ежемесячный платеж (без процентов) составляет х рублей. Тогда кредит был выдан в размере 25х рублей. Банку нужно вернуть эти 25х рублей плюс проценты за остаток вклада каждый месяц: 1-й месяц это 25х ∙ (r/100) ;
во 2-й месяц проценты на остаток вклада составят 24х ∙ (r/100) ;
в 3-й месяц проценты на остаток вклада составят 23х ∙ (r/100) ;
в 4-й месяц проценты на остаток вклада составят 22х ∙ (r/100) ;
…………………………………………………………………………..
во 24-й месяц проценты на остаток вклада составят 2х ∙ (r/100) ;
в последний 25-й месяц проценты на остаток вклада составят х ∙ (r/100) .
Общая сумма денег, которую нужно выплатить банку за весь срок кредитования:
25х + (25х+24х+23х+22х+…+х) ∙ (r/100) =
![]()
По условию общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 13% больше, чем сумма, взятая в кредит. Получаем равенство:
![]()
Разделим обе части равенства на 25х и получим:
![]()
Ответ: 1.
31 декабря 2014 года Арсений взял в банке 1 млн рублей в кредит
Задача. 31 декабря 2014 года Арсений взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определенное число процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?
Решение. Рассмотрим два способа решения задачи.
1 способ. С помощью формулы.
Применим формулу:
![]()
Здесь S – сумма кредита, выданная банком, которая полностью погашается за n
![]()
осуществленных после начисления r% по вкладу. У нас n = 2, тогда формула примет вид:

Подставляем все данные в формулу:
![]()
Разделим обе части равенства на 100 и приведем его к общему знаменателю.
10000(1+0,01r)2 = 5500(1+0,01r) + 6384. Делим обе части равенства на 4.
2500(1+0,01r)2 = 1375(1+0,01r) + 1596. Обозначим 1+0,01r через а. Получаем:
2500а2 = 1375а + 1596 → 2500а2-1375а-1596 = 0.
Дискриминант D = 13752-4 ∙ 2500 ∙ (-1596) = 1890625+15960000 = 17850625;
D = 42252 > 0; уравнение имеет два действительных корня.
Как вручную извлекать квадратные корни из целого числа смотрите здесь.

Мы получили а = 1+0,01r = 1,12 → 0,01r = 0,12 → r = 0,12 : 0,01 = 12.
Ответ: 12.
2 способ. Рассуждения по смыслу задачи.
Обозначим взятую в кредит сумму через S (у нас S=1 млн рублей), а через r – искомый процент банка.
1-ый год. Банк начисляет r% к взятой сумме, и сумма долга составит 100% + r% от S. Чтобы найти проценты от числа нужно обратить проценты в дробь и умножить эту дробь на данное число.
100% + r% =1+0,01r. Обозначим это выражение через k. Итак, 1+0,01r= k.
Умножаем k на S. Получаем Sk. Арсений переводит в банк 550 тысяч рублей. Считать будем в миллионах рублей. Остаток по вкладу равен Sk-0,55.
2-ой год. Банк начисляет r% к остатку, т.е. Арсений теперь должен 100% + r% от (Sk-0,55). Это составит (1+0,01r) или k от (Sk-0,55), т.е. составит k(Sk-0,55). Арсений переводит в банк 638,4 тысяч рублей.
Остаток по вкладу равен k(Sk-0,55)-0,6384. А так как за два года Арсений рассчитался с банком, то получим равенство:
k(Sk-0,55)-0,6384=0. Помним, что S=1 млн рублей.
k(k-0,55)-0,6384=0;
k2-0,55k-0,6384=0. Решаем квадратное уравнение по общей формуле – находим дискриминант.
D=b2-4ac=0,552-4∙1∙(-0,6384)=0,3025+2,5536=2,8561=1,692>0; 2 действительных корня.

1+0,01r=k=1,12; отсюда 0,01r=0,12; r=12.
Ответ: 12%.
Выбор решения за тем, кто решает.
Как вручную извлекают квадратные корни из десятичной дроби смотрите здесь.
31 декабря 2014 года Алексей взял в банке 9282000
Задача. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Рассмотрим два способа решения задачи.
1 способ. С помощью формулы.
Если кредит на S рублей полностью погашается за n ежегодных
![]()
осуществленных после начисления r% по вкладу, то имеет место замечательная формула:
![]()
Кредит Алексея S = 9282000 полностью погашается за 4 платежа по Х рублей каждый, после начисления r = 10% годовых каждый год на оставшуюся сумму долга. Получаем равенство:

Ответ: 2928200.
2 способ. Рассуждения по смыслу задачи.
Обозначим взятую в кредит сумму через S (у нас S=9282000).
1-ый год. Банк начисляет 10% ко взятой сумме, и сумма долга составит 110% от S. Чтобы найти проценты от числа нужно обратить проценты в дробь и умножить эту дробь на данное число.
110%=1,1. Умножаем 1,1 на S. Получаем 1,1S. Алексей переводит в банк Х рублей. Остаток по вкладу равен 1,1S-Х.
2-ой год. Банк начисляет 10% к остатку, т.е. Алексей теперь должен 110% от (1,1S-Х). Это составит 1,1(1,1S-Х). Алексей переводит в банк Х рублей. Остаток по вкладу равен 1,1(1,1S-Х)-Х.
Упростим. 1,12 S-1,1Х-Х=1,21S-2,1Х.
3-ий год. Банк начисляет 10% к остатку, т.е. Алексей теперь должен 110% от (1,21S-2,1Х). Это составит 1,1(1,21S-2,1Х). Алексей переводит в банк Х рублей. Остаток по вкладу равен 1,1(1,21S-2,1Х)-Х.
Упростим. 1,331S-2,31Х-Х=1,331S-3,31Х.
4-ый год. Банк начисляет 10% к остатку, т.е. Алексей теперь должен 110% от (1,331S-3,31Х). Это составит 1,1(1,331S-3,31Х). Алексей переводит в банк Х рублей. Остаток по вкладу равен 1,1(1,331S-3,31Х)-Х.
Упростим. 1,1(1,331S-3,31Х)-Х=1,4641S-3,641Х-Х=1,4641S-4,641Х.
Так как за 4 года Алексей выплатит весь долг, то последняя сумма равна нулю. Решаем уравнение:
1,4641S-4,641Х=0.
4,641Х=1,4641S; помним, что у нас S=9282000. Тогда
Х=(1,4641∙928200):4,641;
![]()
Ответ: 2928200.
Выбор решения исключительно за решающим.
В июле планируется взять кредит в банке на сумму 4,5 млн рублей
Задача. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший – не менее 0,6 млн рублей.
Решение. Как всегда обозначим ежегодный платёж (без процентов) через х. Отсюда сумма кредита будет равна 9х. В этой задаче х = 4,5 млн : 9 = 4500000 : 9 = 500000 рублей.
Мы с вами знаем уже, что самый большой процент приходится на 1-й год выплат. Это r% от 9х, т.е. от всей суммы кредита, получается:
![]()
Таким образом наибольший годовой платёж по кредиту приходится на 1-й год и равен:
![]()
По условию этот платёж должен быть не больше 1,4 млн рублей. Получаем неравенство:
![]()
Вместо х запишем его значение 500000.
![]()
Разделим обе части на 500000.
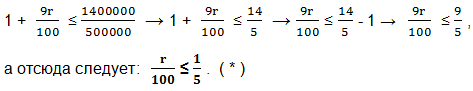
Самый маленький платёж по кредиту будет в последний год, он будет
![]()
и по условию должен быть не меньше 0,6 млн рублей. Получаем:
![]()
Вместо х запишем его значение 500000.
![]()
Разделим обе части на 500000.
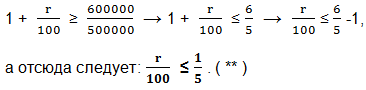
Смотрим на ( * ) и ( ** ). Делаем вывод:
![]()
следовательно, r = 100 : 5 = 20.
Ответ: 20.
15 января планируется взять кредит в банке на сумму 1,8 млн рублей
Задача. 15 января планируется взять кредит в банке на сумму 1,8 млн рублей на 24 месяца. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно вернуть банку в течение первого года кредитования?
Решение. Поймите правильно: «нужно вернуть» не означает, что будет возвращена такая сумма. Если клиент взял кредит на 24 месяца, то на эту сумму ему и будет составлен календарь обязательных ежемесячных равных платежей (вы ведь изучили мои объяснения, приведенные выше?). А это всего лишь задачка на проверку вашего понимания, сколько же процентов будет начислено клиенту за первые 12 месяцев кредитования. Разобьем сумму кредита на 24 части (т.к. 24 месяца кредитования). Получаем: 1800000 : 24 = 75000. Чтобы не таскать это число за собой, обозначим его, как в предыдущих примерах, через х и посчитаем проценты за первые 12 месяцев.
(24х + 23х + 22х + … 13х) ∙ 0,02. Здесь 0,02 – это 2% по условию задачи.
В скобках сумма арифметической прогрессии:
![]()
Так как х = 75000, то выходит, что за первые 12 месяцев сумма процентов составит:
222 ∙ 75000 ∙ 0,02 = 333000 рублей. А выплата по 75000 рублей ежемесячно в течение 12 месяцев составит:
75000 ∙ 12 = 900000 рублей.
Искомое число-сумма выплаты основного долга за 12 месяцев и процентов составляет 900000 + 333000 = 1233000 рублей.
Ответ: 1233000.
15 января планируется взять кредит в банке на 19 месяцев
Задача. 15 января планируется взять кредит в банке на 19 месяцев. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Решение. Пусть ежемесячные выплаты по кредиту (без процентов) составляют х рублей. Тогда сумма кредита составляет 19х рублей. Выплатить нужно эти 19х рублей плюс проценты (как насчитывают проценты смотрите здесь):
![]()
Вручную сумму в скобках считать не стоит. Применим формулу суммы арифметической прогрессии.

Итак, будет выплачена сумма:
![]()
По условию эта сумма на 30% больше суммы, взятой в кредит. Иными словами, эта сумма составляет 130% или 1,3 от 19х. Получаем равенство:
![]()
Разделим обе части равенства на 19х и получим:
![]()
Ответ: 3.
Что необходимо понимать прежде, чем решать задачи на проценты и кредиты ЕГЭ по математике
Попробуем разобраться с механизмом кредитования населения.
Итак, пусть банк выдал кредит в сумме S рублей под r% (1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца) на 24 месяца (для примера берём 24 месяцев). Ежемесячно необходимо выплачивать банку одну и ту же сумму. Как же банк будет «обдирать» клиента (помимо драконовского ссудного процента)? А вот как. Всю сумму кредита (S рублей) банк разделит на количество месяцев займа, т.е. в данном примере на 24. Полученная сумма (обозначим ее через х),
![]()
выплачиваться клиентом. А проценты, спросите вы? Вот тут и начинается самое интересное (для банка, не для клиента!). Банк начисляет r% вначале на всю сумму кредита, т.е. на S рублей или, по нашим обозначениям, на 24х рублей
![]()
Потом банк после выплаты клиентом 1-й раз некоторой суммы, которая будет содержать и проценты, засчитывает выплаченными только х рублей и, считая оставшуюся часть долга 24х-х=23х, насчитывает r% уже на нее. Потом банк, снова получив некоторую сумму от клиента, разумеется, бОльшую х, считает уплаченными только х рублей, а остаток долга равным 23х-х=22х и насчитывает r% на 22х и т.д. Смотрите ТАБЛИЦУ.

Таким образом, в 1-й месяц «набегают» самые большие проценты

Платить придется всю сумму набежавших процентов, т.е.

В скобках сумма арифметической прогрессии, которую можно найти по формуле:
![]()
Следовательно, 24х + 23х + 22х + … + 3х + 2х + х будет равняться:
![]()
Тогда сумма всех процентов за 24 месяца:
![]()
И как же платить эти проценты?
Вот как: получившуюся сумму процентов
банк делит на 24 (количество месяцев займа).
![]()
Банк печатает клиенту календарь выплаты кредита, в которой указывается сумма ежемесячных равных выплат в размере (х+p) рублей. В нашем случае клиент
![]()
чтобы равными долями выплатить сумму кредита S рублей плюс проценты.
В случае оформления кредита на несколько лет (а не месяцев) рассуждаем так же.


