Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два решения
Задача. Найдите все значения параметра а, при каждом из которых уравнение имеет ровно два решения. ![]()
Решение. Найдём область допустимых значений данного уравнения. Под знаком квадратного корня должно быть неотрицательное выражение, поэтому
15 + 2х-х2 ≥ 0. Тогда х2-2х-15 ≤ 0.
Находим корни квадратного уравнения х2-2х-15 = 0 и получаем х1 = -3, х2 = 5. Следовательно, неравенство х2-2х-15 ≤ 0 будет верным при х∈[-3; 5].
ОДЗ: х∈[-3; 5].
Перепишем данное уравнение в виде:
![]()
Левая часть равенства неотрицательна, следовательно и для правой части должно выполняться условие: ах + 4-9а ≥ 0. Так как х может принимать значения от -3 до 5, то наименьшее значение выражения
ах + 4-9а равно а ∙ (-3) + 4-9а = -3а + 4-9а = 4-12а = 0.
![]()
В неравенстве ах + 4-9а ≥ 0 выразим х.
ах ≥ 9а-4. Делим обе части на а. Так как а > 0, то знак неравенства не изменится.
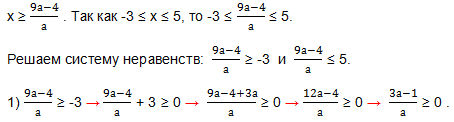
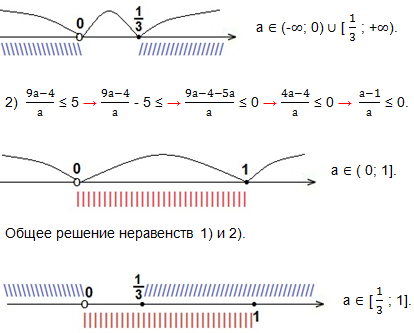
При а = 0 правая часть равна 3.
![]()
Возведём обе части в квадрат.
15 + 2х-х2 = 16. Упростим: х2-2х + 1 = 0 → (х-1)2 = 0.
Отсюда следует, что х = 1 – единственный корень.
Вывод: значение а = 0 также удовлетворяет условию.
![]()


