В правильной треугольной пирамиде МАВС
Задача. В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые рёбра равны 10. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ-точка L. Известно, что АD=АE=LМ=4.
а) Докажите, что отрезок DE содержит центр основания пирамиды.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
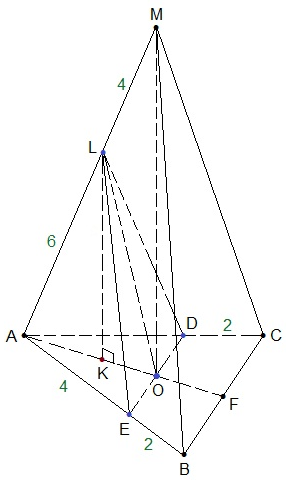Высота данной правильной пирамиды проектируется в центр правильного треугольника АВС – точку пересечения медиан (высот и биссектрис). Обозначим эту точку через О. Мы знаем, что эта точка (пересечения медиан) делит каждую медиану в отношении 2 : 1, считая от вершины, поэтому АО : ОЕ = 2 : 1, что равнозначно отношению АО : АF = 2 : 3. Проводим отрезки DE, DL и LE.
а) Так как DE отсекает от сторон АС и АВ равностороннего треугольника АВС отрезки по 4 см, то ∆ AED ∾ ∆ ABC по двум пропорциональным сторонам и углу между ними, ведь AD : AC = 2 : 3 (на самом деле, 4 : 6 = 2 : 3) и AE : AB = 2 : 3, и общему углу ВАС. Отсюда следует, что ∆AED тоже равносторонний и сторона его DE=AD=AE=4.
Соответствующие медианы подобных треугольников∆ AED и ∆ ABC тоже относятся как 2 : 3, а это и означает, что точка О лежит на отрезке DE.
б) Найдем площадь сечения пирамиды плоскостью, проходящей через точки E, D и L, иначе говоря, найдем площадь треугольника DEL. Проведем LO. В равнобедренном треугольнике DEL медиана LO является и высотой.
Мы знаем только, что DE= 4. Потребуется найти LO.
Проведем LK⟘AF. Прямоугольные треугольники AKL и AOM подобны по общему углу МАО. Справедливо равенство:
Итак, нам лишь потребуется найти МО-высоту пирамиды, которая является катетом в прямоугольном треугольнике АОМ.
Найдем АО, как радиус окружности, описанной около правильного треугольника АВС, по формуле:
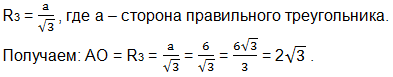
Из треугольника АОМ по теореме Пифагора:
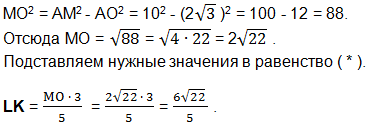
Значение ОК найдем как разность отрезков АО и АК.
Значение АК найдем также из подобия прямоугольных треугольников АОМ и АКL.
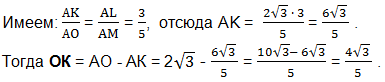
Из прямоугольного треугольника OКL по теореме Пифагора найдем LO.
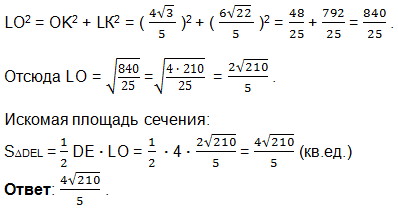
В треугольной пирамиде МАВС основанием является
Задача. В треугольной пирамиде МАВС основанием является правильный треугольник АВС, ребро МВ перпендикулярно плоскости основания, стороны основания равны 3, а ребро МА равно 5. На ребре Ас находится точка D, на ребре АВ находится точка Е, а на ребре АМ -точка L. Известно, что AD=AL=2 и ВЕ=1.
а) Постройте сечение пирамиды LAED плоскостью, проходящей через точку L и перпендикулярное ребру DE.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L.
Решение.
В пирамиде МАВС ребро МВ является высотой. Основание АВС – правильный треугольник со стороной 3.
По условию ребро АМ=5, AD=AL=2 и ВЕ=1. Тогда АЕ=АВ-ВЕ=3-1=2.
В прямоугольном треугольнике АВМ гипотенуза АМ=5, катет АВ=3, тогда катет МB=4 (египетский треугольник, т.е. треугольник со сторонами 3, 4 и 5).
а) Построим сечение пирамиды LAED плоскостью проходящей через точку L и перпендикулярное ребру DE.
Заметим, что основание этой этой пирамиды ADE-равносторонний треугольник со стороной 2. На самом деле: отрезок DE отсекает от каждой из сторон АС и АЕ отрезки по 2 см.
Следовательно, ∆ADE∾∆ACB по двум пропорциональным сторонам и углу между ними. Поэтому ∆ADE также является равносторонним со стороной 2.
Построение сечения: проведем LF⟘AB. Так как LF лежит в грани МАВ, перпендикулярной основанию АВС, то LF является высотой пирамиды LAED.
Из точки F опустим перпендикуляр FK на ребро DE, и точку К соединим с точкой L. По ТТП (теореме о трех перпендикулярах) LK⟘DE (LK-наклонная к плоскости ADE, KF-её проекция, DE-прямая на плоскости, проведенная через основание наклонной перпендикулярно её проекции).
Так как DE⟘ FK и DE⟘ LK, то DE перпендикулярно плоскости LFK.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Таким образом, LFK-сечение пирамиды LAED плоскостью, проходящей через точку L перпендикулярно DЕ.
б) Найдем площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L, т.е. площадь треугольника DEL, которая будет равна половине произведения стороны DE на высоту LK, проведенную к этой стороне.
Так как LK-гипотенуза в прямоугольном треугольнике LFK, то потребуется найти катеты LF и FK.
∆ ABM ∾ ∆ AFL, как прямоугольные треугольники, имеющие один общий острый угол А. Отсюда
Из прямоугольного ∆AFL по теореме Пифагора находим:
Мы уже установили, что треугольник ADE, подобный треугольнику АВС, является равносторонним. Все углы равностороннего треугольника равны 60°. Из прямоугольного треугольника EKF следует:
Искомая площадь сечения:
В правильной треугольной пирамиде МАВС с основанием АВС
Задача. В правильной треугольной пирамиде МАВС с основанием АВС стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре АМ – точка L. Известно, что СD=ВE=LА=2.
а) Докажите, что отрезок DE содержит центр основания пирамиды.
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
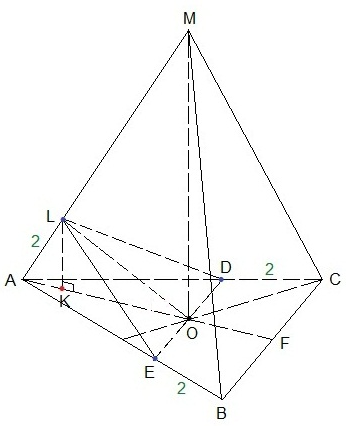а) В равностороннем треугольнике АВС, CD=BE=2 по условию, следовательно,
AD=AE=4. Треугольники ADE и ABC подобны по общему углу ВАС и соответственно пропорциональным сторонам этого угла:
Соответственные высоты этих подобных треугольников относятся друг к другу так же, т.е. АО : AF = 2 : 3.
Это означает, что точка О – середина отрезка DE, делит отрезок AF в отношении 2 : 1, считая от вершины. Следовательно, точка О является точкой пересечения медиан правильного треугольника АВС, т.е. центром основания пирамиды. Мы доказали, что отрезок DE содержит центр основания пирамиды.
б) Проведем отрезки LE и LD.
∆ DEL — сечение пирамиды плоскостью, проходящей через точки E, D и L. Требуется найти площадь этого сечения, т.е. площадь треугольника DEL. Проведем отрезок LO, этот отрезок является медианой, а, значит, и высотой равнобедренного треугольника DEL. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Проведем LK ⟘АО и получим прямоугольный ∆ LOK, из которого можно будет найти LO. Также потребуется найти DE.
Нам нужно найти и LK и OK.
Значение LK найдем из подобия прямоугольных треугольников АОМ и АКL.
Итак, нам лишь потребуется найти МО – высоту пирамиды, которая является катетом в прямоугольном треугольнике АОМ.
Найдем АО, как радиус окружности, описанной около правильного треугольника АВС, по формуле:
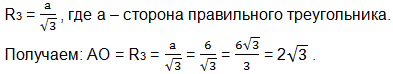
Из треугольника АОМ по теореме Пифагора:
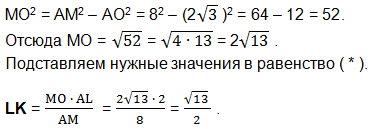
Значение ОК найдем как разность отрезков АО и АК.
Значение АК найдем также из подобия прямоугольных треугольников АОМ и АКL.
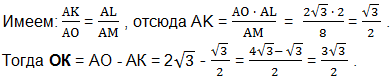
Из прямоугольного треугольника LOК по теореме Пифагора найдем LO.
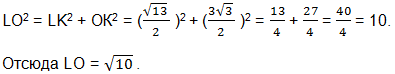
Осталось найти DE. Из подобия треугольников АВС и AED следует, что
