В правильной треугольной призме на рёбрах АС и ВС отмечены соответствующие точки M и N
Задача.
В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответствующие точки M и N так, что AM : MC = CN : BN = 2 : 1,
точка К – середина ребра А1С1.
а) Докажите, что плоскость MNK проходит через вершину В1.
б) Найдите расстояние от точки С до плоскости KMN, если АВ = 6, АА1 = 2,4.
Решение.
а) В основании призмы лежит равносторонний треугольник АВС. Обозначим его сторону через а. Смотрите рис. 1.
Тогда АМ = 2а/3, МС = а/3 и
CN = 2а/3, BN = а/3.
А1К = КС1 = а/2.
Проведём MN и КМ. Это линии пересечения плоскости MNK с нижним основанием призмы и боковой гранью АА1С1С соответственно.
Проведём KF Ʇ AC, тогда AF = FC = a/2. А так как МС = а/3, то
MF = FC-MC = a/2-a/3 = a/6
Проведём В1K и BF.
Четырёхугольник BFKB1 является прямоугольником, отсюда В1K = BF.
В равностороннем треугольнике АВС медиана BF является и высотой.
Таким образом, BF Ʇ AC.
Имеем: MC : FC = a/3 : a/2 = 2 : 3 и CN : BC = 2a/3 : a = 2 : 3.
Треугольники MCN и FCB подобны по двум пропорциональным сторонам и общему углу С между ними. Соответственные углы подобных треугольников равны, поэтому прямые MN и BF параллельны по признаку параллельности прямых. Но BF и В1К параллельны, как противоположные стороны прямоугольника BFKB1, следовательно, параллельны и прямые MN и В1K.
Итак, плоскость MNK пересекает параллельные плоскости нижнего и верхнего основания по параллельным прямым MN и В1K, а так как через точку К можно провести единственную прямую параллельную данной, то очевидно, что плоскость MNK проходит через вершину В1, ч.т.д. Четырёхугольник MNB1K – плоскость сечения данной призмы.
б) Способ 1 (традиционный). Мы доказали, что прямые MN и BF параллельны,
а так как BF Ʇ АС, то и MN Ʇ АС. Для того, чтобы найти расстояние от точки С до плоскости KMN, определим плоскость, проходящую через точку С и перпендикулярную плоскости KMN. Проведём СК и рассмотрим плоскость МСК. Смотрите рис. 2.
На основании теоремы о трёх перпендикулярах MN Ʇ KM (MN – прямая, проведённая на плоскости через основание наклонной КМ, перпендикулярно её проекции FM).
Итак, MN Ʇ KM и MN Ʇ MC, следовательно, MN Ʇ (MCK). Плоскость MNK проходит через прямую MN, перпендикулярную плоскости MСK, а потому будет перпендикулярна плоскости MCK. Так как плоскость МСК перпендикулярна плоскости MNK и пересекает её по прямой МК, то расстоянием от точки С до плоскости KMN будет длина перпендикуляра, проведённого из точки С к прямой МК.
Треугольник МСК тупоугольный (угол СМК тупой, так как является смежным с острым углом KMF), поэтому точка Т — основание перпендикуляра СТ будет лежать на продолжении стороны МК треугольника МСК. Обозначим угол СМТ через α. Тогда и угол KMF равен α (вертикальные углы равны). В прямоугольном треугольнике СТM катет СТ = МС ∙ sinα,
где sinα = KF/MK из прямоугольного треугольника KFM.
По условию АВ = а = 6 и АА1 = 2,4.
Тогда МС = а/3 = 2; MF = a/6 = 1; KF = АА1 = 2,4.
Из прямоугольного треугольника KFM по теореме Пифагора
MK2 = MF2 + KF2 = 12 + 2,42 = 1 + 5,76 = 6,76. Отсюда MK = 2,6.
Получаем sinα = KF/MK = 2,4 : 2,6 = 12/13.
Искомый отрезок СТ = МС ∙ sinα = 2 ∙ 12/13 = 24/13. Это и есть расстояние от точки С до плоскости KMN.
Примечание. СТ можно было найти и без применения тригонометрии. Из подобия прямоугольных треугольников KFM и СТМ по острому углу α справедливо равенство
KF : CT = KM : MC, из которого и находим СТ.
Ответ: 24/13.
б) Способ 2 (метод координат в пространстве).
Решение.
Введём систему координат, считая точку F началом координат, a отрезки FC, FB и FK, лежащими соответственно на осях абсцисс, ординат и аппликат.
Смотрите рис. 3.
Точка М имеет координаты (1; 0; 0), так как MF = a/6 = 6 : 6 = 1.
Точка К имеет координаты (0; 0; 2,4), так как KF = АА1 = 2,4.
Точка С имеет координаты (3; 0; 0), так как FC = a/2 = 6 : 2 = 3.
Плоскость KMN параллельна оси Оу и отсекает от оси Ох отрезок равный 1, а от оси Оz отрезок, равный 2,4. Следовательно, плоскость KMN задаётся уравнением
которое равносильно уравнению 2,4x + z = 2,4 или 2,4x + z -2,4 = 0.
Требуется найти расстояние от точки С(3; 0; 0) до плоскости 2,4x + z -2,4 = 0.
Расстояние h от точки с координатами (xo; yo; zo)
до плоскости ax + by + cz + d = 0 определяется по формуле:
У нас х0 = 3, у0 = z0 = 0; а = 2,4; b = 0, c = 1, d = -2,4.
Тогда искомое расстояние от точки С до плоскости KMN:
Ответ: 24/13.
Высота цилиндра равна 3, а радиус основания равен 13
Задача. Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
Решение.
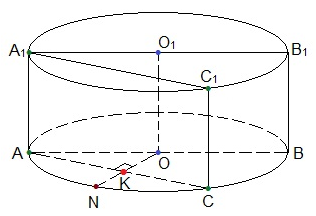Плоскость сечения, параллельная основанию цилиндра представляет собой прямоугольник AA1C1C, площадь которого S = AC ∙ AA1.
Так как по условию Sсеч. = 72
и АА1 = 3, то АС = 72 : 3 = 24.
Заметим, что хорда AC немногим меньше диаметра основания цилиндра (АВ = 2R = 2 ∙ 13 = 26).
Так как плоскость АА1С параллельна оси цилиндра ОО1, то расстояние до нее от точки О — длина перпендикуляра, проведенного из точки О к АС.
Проведем радиус ON перпендикулярно хорде AC.
Радиус, перпендикулярный хорде, делит ее и стягиваемую ею дугу пополам.
Точка K — середина AC, поэтому АК = АС : 2 = 24 : 2 = 12.
OK – искомый отрезок.
Рассмотрим прямоугольный треугольник АКО. По теореме Пифагора:
ОК2 = АО2 – АК2 = 132 – 122 =169 – 144 = 25, отсюда ОК = 5.
Это и есть расстояние от плоского сечения до центра основания цилиндра.
Ответ: 5.
