Задача. Найдите все значения а, при каждом из которых множество значений функции содержит отрезок [0; 1]
Задача. Найдите все значения а, при каждом из которых множество значений функции
![]()
Решение. Отрезок [0; 1] содержится в множестве значений данной функции тогда и только тогда, когда уравнения
![]()
имеют решения. Решаем каждое из этих уравнений.
![]()
Знаменатель этой дроби можно записать в виде:
(10х+а)2+15. Это выражение при любых а и х положительно, поэтому данная дробь будет равна нулю, если числитель дроби будет равен нулю.
5а+150х-10ах=0 → а+30х-2ах=0 → 2х(а-15)=а. Это уравнение имеет решение при любом а ≠ 15.
![]()
Умножим обе части равенства на знаменатель дроби.
5а+150х-10ах=100х2+20ах+а2+25. Упростим это выражение.
100х2+20ах+а2+25-5а-150х+10ах=0 → 100х2+30ах-150х+а2-5а+25=0;
100х2+2(15а-75)х+а2-5а+25=0. Это уравнение имеет решение тогда и только тогда, когда его дискриминант неотрицателен.
![]()
D1 = 225a2-2250a+5625-100a2+500a-2500=125a2-1750a+3125=125(a2-14a+25)≥0. Решим уравнение a2-14a+25=0. Дискриминант этого уравнения
D’=72-25=49-25=24.
Тогда корни уравнения
![]()
Решениями неравенства (a2-14a+25)≥0
служит множество значений переменной а, удовлетворяющих условию
![]()
Исключаем из этих промежутков значение а ≠ 15.
![]()
Найдите все значения параметра а, при каждом из которых множество значений данной функции содержит отрезок [2; 3].
Задача. Найдите все значения параметра а, при каждом из которых множество значений
![]()
Решение. ОДЗ. a ≥ -1. Преобразуем функцию.
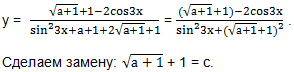
Так как наименьшее значение а = -1, то наименьшее значение с = 1.
![]()
По условию необходимо, чтобы у [2; 3],

Знаменатель этой дроби положителен при любых значениях х и с, поэтому, и числитель дроби должен быть неотрицателен.
c-2cos3x-2(sin23x + c2) ≥ 0 → c-2cos3x-2(1-cos23x)-2c2 ≥ 0;
c -2cos3x-2 + 2cos23x-2c2 ≥ 0 → 2cos23x-2cos3x + c-2c2-2 ≥ 0.
Сделаем замену: cos3x = z. Получаем неравенство: 2z2-2z + c-2c2-2 ≥ 0. ( * )
Решим уравнение: 2z2-2z + c-2c2-2 = 0. ( ** )
Найдём дискриминант D1 = 1-2(c-2c2-2) = 1-2с + 4с2 + 4 = 4с2-2с + 5 > 0 при любом значении с. Корни уравнения ( ** ):
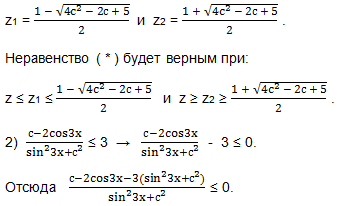
Знаменатель этой дроби положителен при любых значениях х и с, поэтому, и числитель дроби должен быть неотрицателен.
c-2cos3x-3(sin23x + c2) ≤ 0 → c-2cos3x-3(1-cos23x)-3c2 ≤ 0;
c-2cos3x-3 + 3cos23x-2c2 ≤ 0 → 3cos23x-2cos3x + c-3c2-3 ≤ 0.
Сделаем замену: cos3x = z. Получаем неравенство: 3z2-2z + c-3c2-3 ≤ 0. ( *** )
Решим уравнение: 3z2-2z + c-3c2-3 = 0. ( **** )
Найдём дискриминант D1 = 1-3(c-3c2-3) = 1-3с + 9с2 + 9 = 9с2-3с + 10 > 0 при любом значении с. Корни уравнения ( **** ):
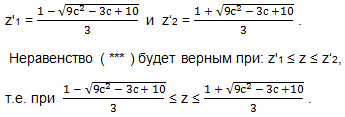
3) Чтобы найти общее решение неравенств ( * ) и ( *** ) нужно правильно расположить числа
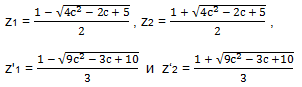
на числовой прямой. Для определённости подставим с = 1 в каждое из выражений и получим:
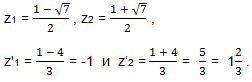
Очевидно, что z’1 ≤ z1 ≤ z2 ≤ z‘2 . Отмечаем эти числа на числовой прямой.
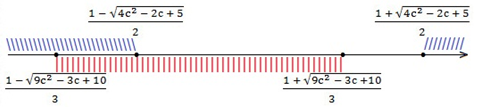
Двойная штриховка показывает общее решение неравенств ( * ) и ( *** ).
Итак, мы получили: z’1 ≤ z ≤ z1,
![]()
Так как z = cos3x, а-1 ≤ cos3x ≤ 1, то -1 ≤ z ≤ 1, то есть необходимо, чтобы
![]()
Решаем первое неравенство.
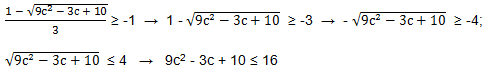
(помним, что 9с2-3с + 10 > 0 при любом значении с).
9с2-3с-6 ≤ 0 → 3с2-с-2 ≤ 0.
Найдём корни уравнения 3с2-с-2 = 0. Дискриминант D = 1-4 ∙ 3 ∙ (-2) = 25.
![]()
Неравенство 3с2-с-2 ≤ 0 выполняется при
![]()
Решаем второе неравенство.
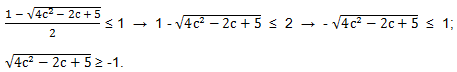
Это неравенство верно при любых значениях с
( а что неравенство 4с2-2с + 5 > 0 при любом значении с мы помним).
Итак, неравенство:
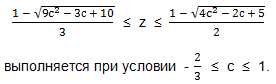
Так как наименьшее возможное значение с = 1, то получаем
![]()
Ответ: а = -1.


