Периметр прямоугольника равен 10, а площадь равна 4,5. Найти диагональ прямоугольника
Задача 1. Периметр прямоугольника равен 28, а площадь равна 92. Найти диагональ прямоугольника.
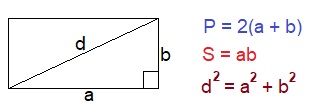
Используйте этот чертёж ко всем следующим задачам.
Решение. Пусть нам дан прямоугольник со сторонами а и b. Нужно найти диагональ прямоугольника d. Диагональ d является гипотенузой прямоугольного треугольника с катетами а и b. На основании теоремы Пифагора d2=a2+b2. Следовательно, необходимо найти a2+b2. По условию периметр прямоугольника равен 28. Так как формула периметра прямоугольника P=2(a+b), то a+b=14. Так как площадь прямоугольника равна S=ab, и по условию S=92, то ab=48. Рассуждаем: сумма чисел а и b равна 14, а произведение 48. Вспоминаем теорему Виета, когда мы подбирали корни квадратного уравнения
x2-14x+48=0 и находили x1=6 и х2=8. В нашем случае а=6 и b=8 или а=8 и b=6. Тогда основании теоремы Пифагора d2=a2+b2. Получаем d2=62+82=36+64=100. Отсюда d=10. Ответ: 10.
Задача 2. Периметр прямоугольника равен 10, а площадь равна 4,5. Найти диагональ прямоугольника.
Решение. Рассуждаем аналогично. Теперь по условию a+b=5, ab=4,5. Понимаем, что числа а и b не будут целыми, и подобрать их не получится. Однако найти требуется диагональ d, которая является является гипотенузой прямоугольного треугольника с катетами а и b. На основании теоремы Пифагора d2=a2+b2. Следовательно, необходимо найти a2+b2, а значения а и b находить по отдельности нет необходимости. Возведём обе части равенства a+b=5 в квадрат. Получим (a+b)2=52. Отсюда a2+2ab+b2=25, тогда a2+b2=25-2ab. Так как ab=4,5, то 2ab=9. Получаем: a2+b2=25-9=16. Значит d2=16, а d=4. Ответ: 4.
Задача 3. Периметр прямоугольника равен 3,6, а площадь равна 0,34. Найти диагональ прямоугольника.
Решение. Рассуждаем аналогично. По условию a+b=1,8, ab=0,34. Диагональ d будет равна квадратному корню из суммы квадратов a2+b2. Возведём обе части равенства a+b=1,8 в квадрат. Получим (a+b)2=(1,8)2. Отсюда a2+2ab+b2=3,24, тогда a2+b2=25-2ab. Так как ab=0,34, то 2ab=0,68. Получаем: a2+b2=3,24-0,68=2,56. Значит d2=2,56, а d=1,6. Ответ: 1,6.
Задача 4. Диагональ прямоугольника равна 5, а площадь равна 5,5. Найти периметр прямоугольника.
Решение. Используем рассуждения предыдущих задач. В этой задаче d=5, а по теореме Пифагора гипотенуза d равна сумме квадратов катетов а и b прямоугольного треугольника (смотрите рисунок), значит, d2=a2+b2=25. Площадь прямоугольника S=ab, и по условию равна 5,5. Значит, ab=5,5; тогда 2ab=11. Требуется найти периметр прямоугольника. Так как по формуле периметр P=2(a+b), то достаточно найти сумму смежных сторон прямоугольника (a+b). Имея a2+b2=25 и 2ab=11, сложим эти два равенства почленно. Получаем:
a2+2ab+b2=25+11, отсюда (a+b)2=36, a+b=6. Так как сумма смежных сторон прямоугольника равна 6, то периметр будет равен 12. Ответ: 12.
Задача 5. Диагональ прямоугольника равна 7, а площадь равна 7,5. Найти периметр прямоугольника. Задача совершенно такая же, как предыдущая задача 4, только числа другие. Решите задачу 5 самостоятельно. Ответ: 16.
Задача 6. Диагональ прямоугольника равна 9, а его периметр равен 22. Найти площадь прямоугольника.
Решение. Используем рассуждения предыдущих задач. Стороны прямоугольника а и b являются катетами прямоугольного треугольника, а диагональ прямоугольника d – гипотенузой этого прямоугольного треугольника. На основании теоремы Пифагора d2=a2+b2 , значит, так как d2=92=81, то a2+b2=81. По условию периметр прямоугольника равен 22, следовательно, полупериметр a+b=11. Возведём в квадрат обе части последнего равенства и получим:
a2+2ab+b2=121, отсюда 2ab=121-(a2+b2)=121-81=40. Площадь квадрата S=ab=40:2=20. Ответ: 20.
Задача 7. Диагональ прямоугольника равна 11, а его периметр равен 24. Найти площадь прямоугольника. Задача совершенно такая же, как предыдущая задача 6, только числа другие. Решите задачу 7 самостоятельно. Ответ: 11,5.
Делаем выводы. Для того чтобы найти диагональ, периметр или площадь прямоугольника не всегда является необходимым находить стороны прямоугольника по отдельности. Чётко ставьте себе задачу, исходя из её условий, и вы найдёте рациональное решение.
Навигация
Предыдущая статья: ← Основание пирамиды SABC — равносторонний треугольник
Следующая статья: Тригонометрические уравнения на ЕГЭ →



Комментирование закрыто.