В июле планируется взять кредит в банке на сумму 4,5 млн рублей
Задача. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший – не менее 0,6 млн рублей.
Решение. Как всегда обозначим ежегодный платёж (без процентов) через х. Отсюда сумма кредита будет равна 9х. В этой задаче х = 4,5 млн : 9 = 4500000 : 9 = 500000 рублей.
Мы с вами знаем уже, что самый большой процент приходится на 1-й год выплат. Это r% от 9х, т.е. от всей суммы кредита, получается:
![]()
Таким образом наибольший годовой платёж по кредиту приходится на 1-й год и равен:
![]()
По условию этот платёж должен быть не больше 1,4 млн рублей. Получаем неравенство:
![]()
Вместо х запишем его значение 500000.
![]()
Разделим обе части на 500000.
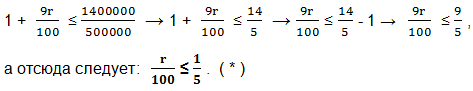
Самый маленький платёж по кредиту будет в последний год, он будет
![]()
и по условию должен быть не меньше 0,6 млн рублей. Получаем:
![]()
Вместо х запишем его значение 500000.
![]()
Разделим обе части на 500000.
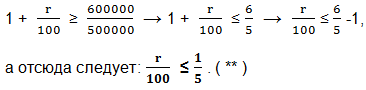
Смотрим на ( * ) и ( ** ). Делаем вывод:
![]()
следовательно, r = 100 : 5 = 20.
Ответ: 20.


