В правильной четырёхугольной пирамиде SABCD все рёбра равны 1
Задача. В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F-середина ребра SВ, G-середина ребра SC.
а) Постройте прямую пересечения плоскостей ABG и GDF.
б) Найдите угол между плоскостями ABG и GDF.
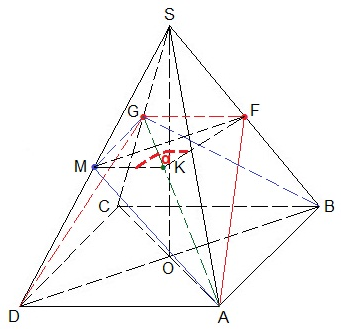 Решение. а) Строим плоскость ABG. Соединим B и G. Плоскость ABG пересекает основание по АВ. Грань SBC — по прямой BG. Плоскость ABG имеет с плоскостью SCD общую точку G, значит, должна пересекать грань SCD по прямой, проходящей через G, причем, эта прямая не может пересечь CD, так как CD лежит основании АВCD, а плоскость ABG пересекает основание пирамиды по прямой АВ, поэтому ни одна точка прямой CD не будет принадлежать АВ, ведь АВ || CD. Вывод: прямой пересечения плоскости ABG с гранью SCD будет прямая MG, не пересекающая ребро CD. Проводим MG || CD. Отметим, что MG || АВ.
Решение. а) Строим плоскость ABG. Соединим B и G. Плоскость ABG пересекает основание по АВ. Грань SBC — по прямой BG. Плоскость ABG имеет с плоскостью SCD общую точку G, значит, должна пересекать грань SCD по прямой, проходящей через G, причем, эта прямая не может пересечь CD, так как CD лежит основании АВCD, а плоскость ABG пересекает основание пирамиды по прямой АВ, поэтому ни одна точка прямой CD не будет принадлежать АВ, ведь АВ || CD. Вывод: прямой пересечения плоскости ABG с гранью SCD будет прямая MG, не пересекающая ребро CD. Проводим MG || CD. Отметим, что MG || АВ.
Плоскость ABG будет пересекать грань SAD по прямой AM.
Плоскость ABG – равнобокая трапеция AMGB.
Строим плоскость GDF. Проведем DG – прямая пересчения плоскости GDF с гранью SCD. Соединим G и F – прямая пересечения с гранью SBC. GF не пересекает BC, так как по построению является средней линией треугольника SBC, следовательно, не пересечет и AD, то есть AD-прямая пересечения плоскости GDF с основанием пирамиды. AF-прямая пересечения с гранью SAB.
Мы получим точно такую же равнобокую трапецию ADGF. Почему трапеции равны? Большее основание – сторона квадрата. Меньшее основание – средняя линия равностороннего треугольника. Боковые стороны трапеция есть медианы равносторонних треугольников-боковых граней пирамиды. Эти две трапеции AMGB и ADGF имеют 2 общие точки A и G, следовательно, пересекаются по прямой AG. Итак, AG — прямая пересечения плоскостей ABG и GDF.
б) Найдем угол между плоскостями ABG и GDF.
AG – общая диагональ наших равных трапеций. Это линия пересечения плоскостей ABG и GDF.
Угол между двумя плоскостями называют угол, образованный двумя полупрямыми, перпендикулярными линии пересечения этих плоскостей.
Проведем MK⟘AG и точку К соединим с F. Получим, что FK⟘AG, так как МК и FK – это равные высоты в равных треугольниках AMG и AFG, проведенные из равных углов к общей стороне AG , которая является общей диагональю равных равнобоких трапеций AMGB и ADGF. Найдем угол MKF – линейный угол между плоскостями ABG и GDF. Соединим M и F. Обозначим ∠MKF через α и рассмотрим ∆MKF. На основании теоремы косинусов имеем:
![]()
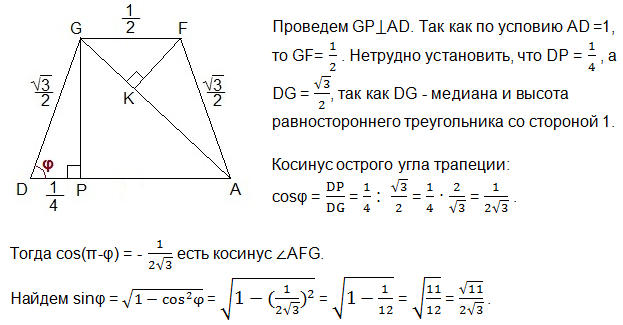
Из треугольника ADG найдем AG по теореме косинусов:
AG2 = AD2 + DG2 -2 ∙ AD ∙ DG ∙ cosφ;
![]()
MK и KF – равные высоты, найдем через площадь треугольника AFG.
![]()
Подставляем имеющиеся данные и получаем:



