Основание пирамиды SABC — равносторонний треугольник
Задача. Основание пирамиды SABC — равносторонний треугольник АВС. Боковое ребро SA перпендикулярно плоскости основания, точки М и N — середины рёбер ВС и АВ соответственно, причём SN=AM.
а) Докажите, что угол между прямыми АМ и SN равен 60°.
б) Найдите расстояние между этими прямыми,
![]()
Решение.
а) Докажем, что угол между прямыми АМ и SN равен 60°. Прямые АМ и SN являются скрещивающимися.
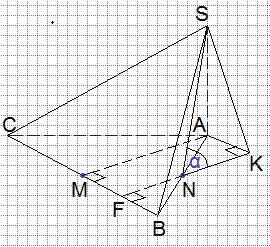 Углом между скрещивающимися прямыми считают угол между соответственно параллельными им пересекающимися прямыми.
Углом между скрещивающимися прямыми считают угол между соответственно параллельными им пересекающимися прямыми.
Прямую АМ заменим параллельной ей прямой FN. Углом между скрещивающимися прямыми АМ и SN будет угол между пересекающимися прямыми FN и SN. Обозначим этот угол через α и докажем, что он равен 60°.
Проведём АК параллельно ВС. Соединим точки S и К. Так как точка М – середина ВС, а треугольник АВС равносторонний, то АМ – медиана, высота и биссектриса треугольника АВС. Тогда прямая FK, параллельная АМ будет также перпендикулярна ВС. А так как АК параллельна ВС, то АК перпендикулярна и АМ, и FK. Таким образом, четырёхугольник АМFК является прямоугольником. Прямая SК является наклонной к плоскости АВС, SА – перпендикуляр к плоскости АВС, АК – проекция прямой SК на плоскость АВС. Прямая FK, проведённая через основание наклонной SК перпендикулярно её проекции АК, будет перпендикулярна наклонной SК на основании теоремы о трёх перпендикулярах. Значит, треугольник SNK является прямоугольным с прямым углом при вершине К. Катет NK равен половине FK, а значит, и половине АМ (противоположные стороны прямоугольника АМFК равны, а равенство отрезков FN и NK следует из равенства прямоугольных треугольников NFB и NKA по равным катетам BN и AN и вертикальным углам при вершине N).
![]()
По условию SN=AM , поэтому
![]()
Итак, из прямоугольного треугольника SNK

Отсюда следует:
![]()
что и требовалось доказать.
б) Найдём расстояние между скрещивающимися прямыми АМ и SN. Используем метод проекций, опирающийся на следующую лемму.
Лемма Шарыгина И.Ф.
Расстояние между скрещивающимися прямыми равно расстоянию от точки, являющейся проекцией одной из прямых на перпендикулярную ей плоскость, до проекции другой прямой на эту плоскость.
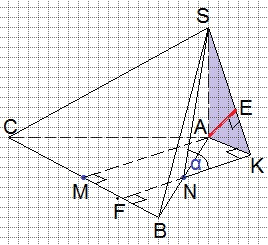 У нас SKA – плоскость, перпендикулярная прямой АМ (АМ перпендикулярна SA по условию и АК по построению). А – проекция АМ на плоскость SKA. SN – наклонная к плоскости SKA, NK – перпендикуляр, SК – проекция наклонной SN к плоскости SKA. Расстояние от точки А до SК и будет являться искомым расстоянием между скрещивающимися прямыми АМ и SN. Проведём АЕ перпендикулярно SК. Отрезок АЕ – это высота прямоугольного треугольника SKA, проведённая к гипотенузе SK.
У нас SKA – плоскость, перпендикулярная прямой АМ (АМ перпендикулярна SA по условию и АК по построению). А – проекция АМ на плоскость SKA. SN – наклонная к плоскости SKA, NK – перпендикуляр, SК – проекция наклонной SN к плоскости SKA. Расстояние от точки А до SК и будет являться искомым расстоянием между скрещивающимися прямыми АМ и SN. Проведём АЕ перпендикулярно SК. Отрезок АЕ – это высота прямоугольного треугольника SKA, проведённая к гипотенузе SK.
![]()
В равностороннем треугольнике АВС
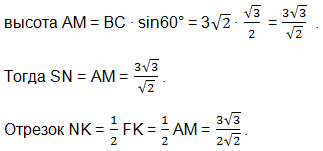
Так как в треугольнике АВМ точка N – середина стороны АВ, FN параллельна АМ, поэтому FN – средняя линия треугольника АВМ. Точка F – середина отрезка ВМ.
![]()
АК = МF как противоположные стороны прямоугольника АМFК.
![]()
В прямоугольном треугольнике SAN гипотенуза
![]()
По теореме Пифагора SA2 = SN2 — AN2.
![]()
Тогда SA = 3.
Из прямоугольного треугольника SKN
катет SK = SN ∙ sinα = SN ∙ sin60°.

Ответ: 1.
Смотрите видео решение этой задачи


