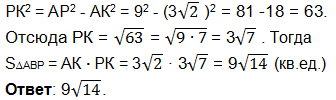Радиус основания конуса с вершиной
Задача. Радиус основания конуса с вершиной Р равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1:3.
а) Постройте сечение конуса плоскостью, проходящей через точки А, В и Р.
б) Найдите площадь сечения конуса плоскостью АВР.
Решение.
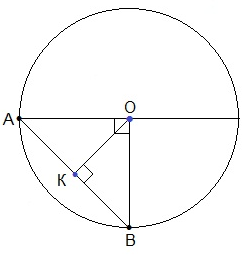 а) Сечение конуса плоскостью, проходящей через точки А, В и Р – это равнобедренный ∆АРВ, основание которого сторона АВ – хорда окружности, стягивающая дугу 90°. А почему? На самом деле, так как по условию, точки А и В делят окружность на две дуги, отношение которых 1 : 3, то меньшая дуга будет равна одной четвёртой части от 360°- градусной меры всей окружности.
а) Сечение конуса плоскостью, проходящей через точки А, В и Р – это равнобедренный ∆АРВ, основание которого сторона АВ – хорда окружности, стягивающая дугу 90°. А почему? На самом деле, так как по условию, точки А и В делят окружность на две дуги, отношение которых 1 : 3, то меньшая дуга будет равна одной четвёртой части от 360°- градусной меры всей окружности.
Далее, имеем треугольник АОВ — прямоугольный равнобедренный с катетом АО=6 (радиус основания конуса). Тогда
![]()
Проведем радиус, перпендикулярный хорде, который пересечет хорду в точке К.
ОК – медиана прямоугольного равнобедренного треугольника АОВ, поэтому,
![]()
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
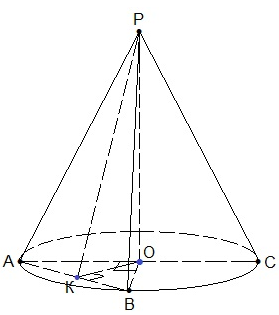 б) Площадь сечения конуса плоскостью АВР -это площадь треугольника АВР, которую найдем как половину произведения его стороны АВ на высоту РК, проведенную к этой стороне.
б) Площадь сечения конуса плоскостью АВР -это площадь треугольника АВР, которую найдем как половину произведения его стороны АВ на высоту РК, проведенную к этой стороне.
![]()
где РК-медиана, а потому и высота равнобедренного треугольника АВР. Из прямоугольного треугольника АКР по теореме Пифагора: