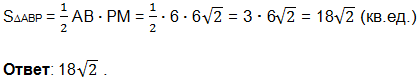Радиус основания конуса с вершиной Р
Задача. Радиус основания конуса с вершиной Р равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1 : 5.
а) Постройте сечение конуса плоскостью, проходящей через точки А, В и Р.
б) Найдите площадь сечения конуса плоскостью АВР.
 Решение.
Решение.
а) Пусть дан конус с осевым сечением РАС и высотой РО. Радиус основания конуса ОА=6, образующая PA=9. Через точки А, В и Р проведено сечение. Это ∆АВР. Так как точки А и В делят окружность на две дуги, длины которых относятся как 1 : 5, то дуга АВ составляет 1/6 часть длины окружности (всего 1+5=6 частей), и поэтому, центральный угол, соответствующий дуге АВ также составляет 1/6 часть угловой меры окружности.
![]()
Получается, что треугольник АОВ-равносторонний, и АВ=ОВ=ОА=6.
б) Проведем ОМ⟘АВ. Точка М-середина хорды АВ (радиус, перпендикулярный хорде делит её и стягиваемую ею дугу пополам).
Таким образом, АМ=ВМ=АВ : 2 = 6 : 2 = 3.
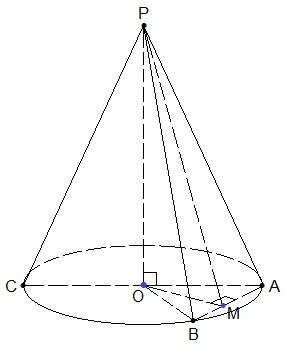
В равнобедренном треугольнике АВР с основанием АВ медиана РМ является и высотой. Площадь треугольника АВР равна половине произведения АВ на высоту треугольника РМ.
РМ-катет в прямоугольном ∆АМР. По теореме Пифагора:
РМ2 = РА2 -АМ2 = 92— 32 = 81- 27 = 72, отсюда
![]()
Искомая площадь сечения конуса плоскостью АВР: