Производная. Часть 1
Определение понятия производной и её геометрического смысла
показано на рисунке 1, а подробно раскрыто в видео, которое можно посмотреть на
YouTube: https://youtu.be/OniFjwZ3b00
RUTUBE: https://rutube.ru/video/0fd4e77d6cd661ed4d2cbc1c96137f10/
ЯндексДзен: https://zen.yandex.ru/video/watch/623be27502c2cc69a1db251a
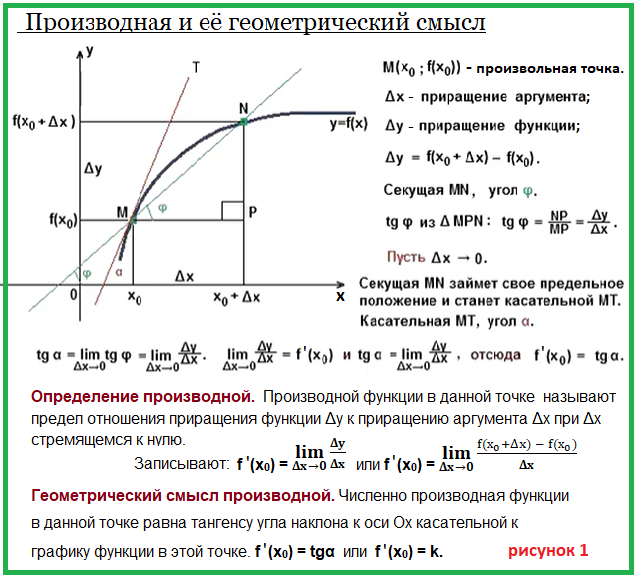
Поясним новые понятия.
Приращение аргумента Δх и приращение функции Δу.
Во-первых, для функции y = f(x)
х –аргумент; у – функция.
Приращение аргумента Δх — это величина, на которую изменяют (увеличивают, как на рисунке, или уменьшают) абсциссу х0 произвольной точки М графика, причём значение Δх незначительно отличается от зафиксированного значения х0.
В результате получается новое значение аргумента х = х0 + Δх. Этому новому значению аргумента соответствует новая точка графика N,
у которой координаты (x0+Δx; f(x0+Δx)). Что же получилось? Мы увеличили абсциссу точки М на Δх и в результате ордината увеличилась на Δу = f(x0+Δx) -f(x0).
Что такое lim.
В переводе limit – предел, предельное значение при определённом условии.
Что означает знак ( ′ ) штрих. Это знак производной.
f(x) – функция; f ′(x) – производная функции.
![]()
производная функции f в точке х0 равна пределу отношения приращения функции Δу к приращению аргумента Δх при Δх стремящемся к нулю.
В чём заключается геометрический смысл производной?
Производная функции в данной точке есть угловой коэффициент
прямой у = kx + b (на рисунке прямая МТ), которая служит касательной
к графику функции y = f(x) в точке с абсциссой х0.
А так как коэффициент k = tgα, где α – угол между касательной и положительным направлением оси Ох, то имеем равенство:
f ′(x0) = k = tgα. В этом и состоит геометрический смысл производной.
Используя равенство f ′(x0) = tgα, вы легко решите такие задания ЕГЭ,
как задача 6 ЕГЭ 2022 ФИПИ.
Примеры.
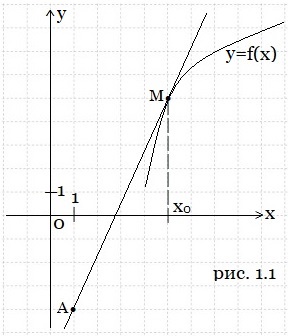
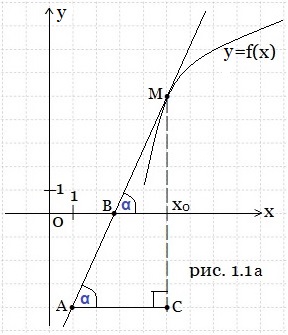
Пример 1. На рисунке 1.1 изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Решение. М – точка касания (рис. 1.1а). Касательная МА пересекает ось Ох в точке В и образует угол МВХ с положительным направлением оси Ох. Обозначим этот угол через α. Искомое значение производной функции f(x) в точке х0 равно тангенсу угла α. Построим прямоугольный треугольник АСМ с гипотенузой МА. Угол МАС также равен α. Найдём тангенс угла α из ΔАСМ. Считаем клеточки (единичные отрезки). МС = 9, АС = 4.
![]()
Так как f ′(x0) = tgα, то получаем f ′(x0) = 2,25.
Ответ: 2,25.
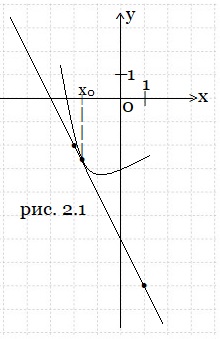
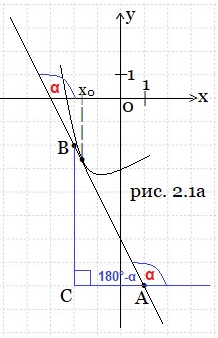
Пример 2. На рисунке 2.1 изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Решение. Касательная АВ (рис. 2.1а) к графику функции y = f(x) в точке х0 образует угол α с положительным направлением оси Ох.
Искомое значение f ′(x0) = tgα. Вначале из прямоугольного треугольника АВС найдём тангенс угла ВАС, смежного с углом α. У нас ВС = 6, АС = 3.
![]()
Нас интересует tgα.
Так как tg(180°-α) = -tgα, то tgα = -tg(180°-α) = -2.
Тогда f ‘(x0) = tgα = -2. Ответ: -2.
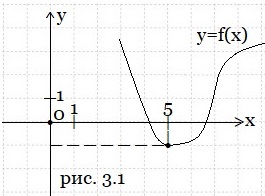
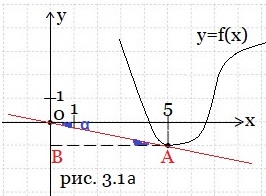
Пример 3. На рисунке 3.1 изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите значение производной функции f(x) в точке х0 = 5.
Решение. Касательная АО (рис. 3.1а) образует тупой угол с положительным направлением оси Ох. Найдём тангенс острого угла α смежного с этим тупым углом, а значения тангенсов смежных углов отличаются лишь знаком.
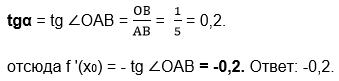

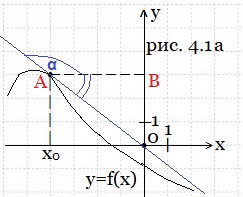
Пример 4. На рисунке 4.1 изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой -4. Найдите значение производной функции f(x) в точке х0 = -4.
Решение. Касательная АО (рис. 4.1а) образует тупой угол α с положительным направлением оси Ох. Найдём тангенс смежного с углом α угла ОАВ из прямоугольного треугольника АВО.
По свойству смежных углов ∠ОАВ=180°-α.
Мы найдём тангенс угла (180°-α) и воспользуемся равенством
tgα = -tg(180°-α).
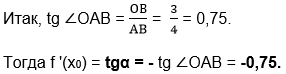
Ответ: -0,75.
Формулы и правила производной
Возникает вопрос. А как находить производную функции, если нет никаких рисунков?
Ответ. По формулам, выведенным согласно определения производной, т.е. на основании равенства:
![]()
Потребуется только равенство y = f(x), где f(x) – выражение, содержащее переменную х.
В качестве примера рассмотрим вывод формулы производной степени.
На основании определения производной получим формулу:
(хn)′ = nxn-1.
Смотрите рисунок 2. Подробности на видео.
YouTube: https://youtu.be/gNqs6svP61A
RUTUBE: https://rutube.ru/video/c2722daedf644bdf1da071fb8656a9b0/
ЯндексДзен: https://zen.yandex.ru/video/watch/623fd665de9aa25e6dd7247c

Итак, мы имеем формулу ( хn )′ = nxn-1.
Примеры. Найти производные следующих функций.
1) у =х6. Решение. у′ = 6х5.
2) у = х. Решение. у′ = 1х0 = 1.
х′ = 1.
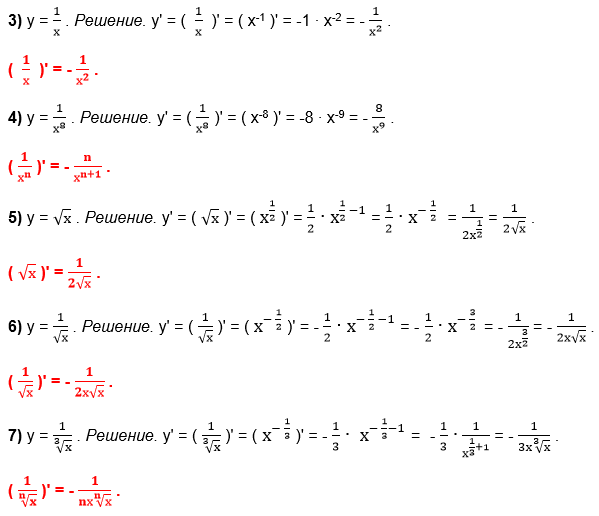
На основании определения производной выводятся и производные других элементарных функций.
Операцию нахождения производной функции называют дифференцированием этой функции.
Вопрос. Многие функции представляют собой сумму, разность, произведение или частное некоторых функций f(x) и g(x). Как быть в этих случаях?
Ответ. Применяют правила дифференцирования, которые выводятся также на основании определения производной функции. Для удобства введём обозначения: u = f(x) и v = g(x).
1. Производная суммы (разности) равна сумме (разности) производных.
(u ± v)′ = u ′ ± v ′
2. Производная произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
(uv)′ = u′v + uv′
3. Постоянный множитель можно вынести за знак производной.
(Сu)′ = Cu′.
4. Производная постоянной величины равна нулю.
С ′ = 0.
5. Производная дроби равна дроби, числитель которой есть произведение производной числителя исходной дроби на знаменатель минус произведение числителя исходной дроби на производную знаменателя, а знаменатель результата равен квадрату знаменателя исходной дроби.
![]()
Сложная функция
Вопрос. Что такое сложная функция? Как найти производную сложной функции?
Ответ. Функцию от функции называют сложной функцией.
Пример 1. Функция у = (2х + 3)7 является сложной, так как это степенная функция от линейной функции.
![]()
Это функция арифметического квадратного корня от квадратичной функции.
В общем виде: функция у = f(u(x)) сложная. Функция f зависит от функции u,
а функция u зависит от х, так что х – аргумент сложной функции.
6. Производную сложной функции f(u(x)) находят по переменной х. Для этого вначале находят производную функции f по переменной u и результат умножают на производную функции u по переменной х.
![]()
Применим эту формулу к функции у = (2х + 3)7 (пример 1).
Здесь f(u) = u7; u(x) = 2x+3.
Тогда у ‘ = 7u6 ∙ (ux)′ = 7(2х + 3)6 ∙ (2х + 3)’ = 7(2х + 3)6 ∙ 2 = 14(2х + 3)6.
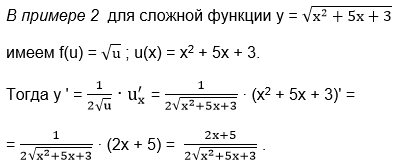
Уравнение касательной
Уравнение касательной к графику функции y=f(x) в точке с абсциссой х0 имеет вид:
y = f(x0) + f ‘(x0)(x —x0). Смотрите рисунок 3.
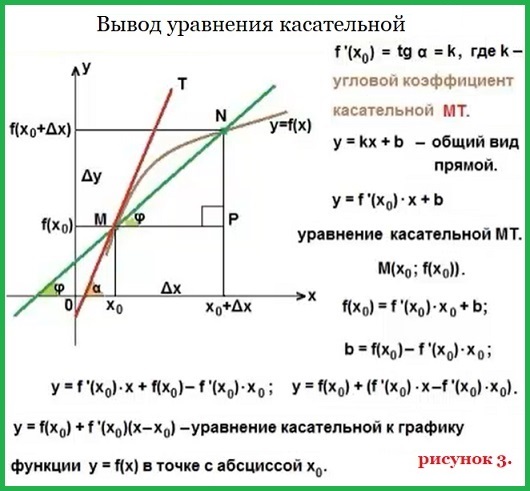
Смотрите видео вывода уравнения касательной.
YouTube: https://youtu.be/F2FGE0njy2U
RUTUBE: https://rutube.ru/video/8ce780b3a7c20e73db21515620c1089f/
ЯндексДзен: https://zen.yandex.ru/video/watch/623d2a7cd1c13971d8c16e66
Пример 1. Написать уравнение касательной к графику функции
у = х3 + 3х в точке с абсциссой х0 = 3.
Решение. Искомое уравнение касательной имеет вид:
y = f(x0) + f ′(x0)(x -x0).
Требуется найти f(x0) и f ‘(x0), а затем подставить найденные значения в уравнение касательной.
f(x0) = f(3) = 33 + 3∙3 = 27 + 9 = 36.
f ′(x) = (х3 + 3х)′ = 3х2 + 3.
f ′(x0) = f ′(3) = 3∙32 + 3 = 30.
Получаем у = 36 + 30(х -3); у = 36 + 30х -90;
у = 30х -54 – искомое уравнение касательной.
Пример 2. Написать уравнение касательной к графику функции
у = -2х2-12х-13 в точке с абсциссой х0 = -4. Сделать рисунок.
Решение. Искомое уравнение касательной имеет вид:
y = f(x0) + f ‘(x0)(x-x0).
Требуется найти f(x0) и f ‘(x0), а затем подставить найденные значения в уравнение касательной.
f(x0) = f(-4) = -2∙(-4)2-12∙(-4)-13 = -32+48-13 = 3.
f ‘(x) = (-2х2-12х-13)’ = -4x-12.
f ‘(x0) = f ‘(-4) = -4∙(-4)-12 = 16-12 = 4.
Получаем у = 3 + 4(х + 4); у = 3 + 4х + 16;
у = 4х + 19 – искомое уравнение касательной.
Сделаем рисунок.
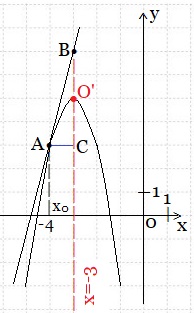 Графиком функции у = -2х2-12х-13 служит парабола с вершиной О’(m; n).
Графиком функции у = -2х2-12х-13 служит парабола с вершиной О’(m; n).
![]()
n = y(m) = y(-3) = -2∙(-3)2-12∙(-3)-13 = -18+36-13 = 5.
О’(-3; 5) – вершина параболы. Ветви параболы направлены вниз, так как отрицателен коэффициент
а = -2 при х2.
От точки (-3; 5) как от начала координат строим параболу у = -х2 (или построим одну-две дополнительные точки и используем свойство симметрии параболы относительно своей оси х = m).
Наша касательная у = 4х +19 касается параболы в точке А(-4; 3). Это одна точка прямой. Если взять х = -3, то получим у = 4∙(-3) + 19 = 7. Это точка В(-3; 7).
Проведём прямую (нашу касательную) через точки А и В.
Задание выполнено. Мы потрудились, а теперь полюбуемся своей работой и вспомним, в чём заключается геометрический смысл производной. Через точку А проведём прямую, параллельную оси Ох до точки пересечения с осью параболы (х = -3), которую обозначим через С. Угол ВАС – это угол между касательной к параболе в точке х0 и положительным направлением оси Ох. Из прямоугольного треугольника АСВ тангенс угла ВАС равен отношению противолежащего катета ВС к прилежащему катету АС и равен 4:1 = 4.
В самом деле, могло ли быть иначе? Так как уравнение нашей касательной
у = 4х + 19, то угловой коэффициент k = tg∠ВАС = 4. И это найденное нами ранее значение f ‘(x0).
Итак, мы убедились на примере:
f ‘(x0) = k = tgα = 4.
Производная функции в данной точке есть угловой коэффициент
прямой у = 4x + 19 (на рисунке прямая АВ), которая служит касательной
к графику функции y = -2х2-12х-13 в точке с абсциссой х0 = -4. В этом суть геометрического смысла производной.
Механический (физический) смысл производной
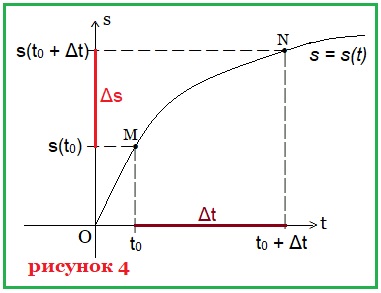 Рассмотрим движение материальной точки по некоторой траектории (рисунок 4).
Рассмотрим движение материальной точки по некоторой траектории (рисунок 4).
На горизонтальной оси Оt мы будем отмечать время пути, а на вертикальной оси Os — расстояние, пройденное точкой за определённое время.
Зафиксируем точку М в момент времени t0.
Пройденный точкой путь на момент времени t0 равен s(t0) — значению функции в точке М.
Если в момент времени t координата материальной точки равна s, где s = s(t), то функцию s(t) называют законом движения материальной точки.
За промежуток времени Δt наша материальная точка совершила перемещение из положения М в положение N. Таким образом в момент времени t = t0 + Δt точкой пройден путь s(t0 + Δt), и, следовательно, за время Δt точка преодолела путь
Δs = s(t0 + Δt) — s(t0).
Среднюю скорость движения точки от М до N определим по формуле
![]()
Средняя скорость тем полнее характеризует движение, чем короче участки пути, на которых она определена. Поэтому один из возможных способов описания неравномерного движения состоит в задании средних скоростей этого движения на всё более и более малых участках пути. Логично, что малые участки пути будут соответствовать малым промежуткам времени.
Пусть Δt стремится к нулю. Это означает, что от времени t0 до времени t = t0 + Δt прошло буквально мгновение, и точка N практически неотличима от точки М.
А что же произойдёт со скоростью ?
Предел этой скорости при Δt → 0 называется мгновенной скоростью движения в момент времени t:
![]()
Знакомо? Да это же определение производной!
Предел отношения приращения пути Δs к приращению времени Δt при Δt стремящимся к нулю есть производная пути s по времени t.
А в результате получилась скорость v(t).
Говорят, что скорость есть производная пути по времени: v(t) = s‘(t).
Аналогично можно показать, что
ускорение есть производная скорости по времени: a(t) = v‘(t).
В последних двух формулировках и заключается механический (физический) смысл производной.
Пример 1. (Задача 6 ЕГЭ) Материальная точка движется прямолинейно по закону
x(t) = t3 + 4t2 -3t + 15, где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 7 с.
Решение.
Так как скорость есть производная пути по времени,
то в нашем случае v(t) = х’ (t) = (t3 + 4t2 -3t + 15)’.
v(t) = 3t2 + 8t-3.
Тогда скорость в момент времени t = 7 найдём, подставив это значение 7 в последнее равенство.
v(7) = 3 ∙ 72 + 8 ∙ 7-3 = 3 ∙ 49 + 56-3 = 200. Ответ: 200.
Пример 2. (Задача 6 ЕГЭ) Материальная точка движется прямолинейно по закону
x(t) = t2 -9t -22, где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) её скорость была равна 3 м/с?
Решение. Скорость есть производная пути по времени, поэтому
v(t) = х’ (t) = (t2 -9t -22)’.
v(t) = 2t -9.
Найдём время t, зная скорость v = 3 в момент этого времени.
3 = 2t -9 → 2t = 12 → t = 6. Ответ: 6.
Пример 3. Точка движется прямолинейно по закону x(t) = 2t3 + t -1.
В какой момент времени ускорение будет равно 6 см/с2?
(x(t) – перемещение в сантиметрах, t – время в секундах.)
Решение. Скорость есть производная пути по времени, поэтому
v(t) = х’ (t) = (2t3 + t -1)’ = 6t2 + 1.
Ускорение есть производная скорости по времени: a(t) = v‘(t).
У нас a(t) = (6t2 + 1)’ = 12t.
Итак, a(t) = 12t. Найдём момент времени t при котором по условию ускорение
a(t) = 6.
6 = 12t → t = 6 : 12 → t = 0,5. Ответ: 0,5.


