Радиус основания конуса с вершиной Р равен 6

Задача. Радиус основания конуса с вершиной Р равен 6, а длина его образующей равна 7. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1:2.

а) Постройте сечение конуса плоскостью, проходящей через точки А, В и Р.

б) Найдите площадь сечения конуса плоскостью АВР.

Решение.

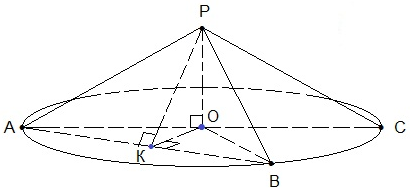Дан конус с осевым сечением РАС и высотой РО. Радиус основания АО=6, длина образующей АР=7. Длина дуги АВ относится к длине дуги АСВ как 1 : 2, т.е. дуга АВ составляет треть длины окружности .

а) Сечение конуса плоскостью, проходящей через точки А, В и Р представляет собой равнобедренный треугольник РАВ с основанием АВ. Хорда АВ видна из центра основания конуса (точки О) под углом 120° (третья часть от 360°).

б) Нам нужно найти площадь ∆РАВ. Проведем из точки О радиус, перпендикулярный хорде АВ. Он пересечет хорду в точке К, которая разделит пополам хорду АВ (радиус, перпендикулярный хорде,делит её и стягиваемую ею дугу пополам). Так как в равнобедренном треугольнике АОВ отрезок ОК-медиана, высота и биссектриса, то ∠ВОК = 120° : 2 = 60°.

Рассмотрим прямоугольный треугольник ОКВ.

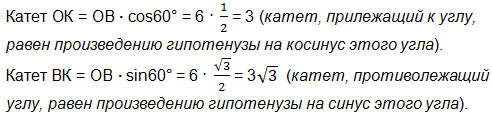
Проведем РК. Это медиана и высота в равнобедренном треугольнике РАВ.

Искомую площадь сечения (площадь ∆РАВ) найдем как половину произведения стороны АВ на высоту РК, проведенную к этой стороне. РК найдем по теореме Пифагора из прямоугольного треугольника АКР. У нас гипотенуза АР=7, катет