Тригонометрические уравнения на ЕГЭ
Пример 1.
а) Решить уравнение cos4x+cos2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-π; π/3].
Решение.
а) Решаем уравнение cos4x+cos2x=0.
Применим формулу ![]()
Tогда данное уравнение примет вид: 2cos3x⋅cosx=0. Отсюда следует, что либо cos3x=0 либо cosx=0.
- Если cos3x=0, то 3х=π/2+πn, отсюда х=π/6+πn/3, где nϵZ.
- Если cosx=0, то х=π/2+πn, где nϵZ.
Заметим, что решения уравнения cosx=0 входят в решения уравнения cos3x=0, поэтому общим решением данного уравнения будут числа x=π/6+πn/3, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [-π; π/3].
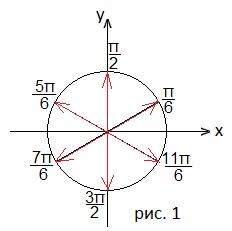
Рассмотрим общее решение x=π/6+πn/3, где nϵZ на единичной окружности. Здесь значение πn/3 означает, что нужно брать n раз угол π/3. Отмечаем угол π/6, а затем углы, полученные поворотом угла π/6 на π/3, полученный таким образом угол π/2 опять повернём на π/3, получится угол 5π/6, затем угол 5π/6+ π/3=7π/6, следующий угол
7π/6+ π/3=9π/6=3π/2, и, наконец, 3π/2+ π/3=11π/6. Смотрите рисунок 1.
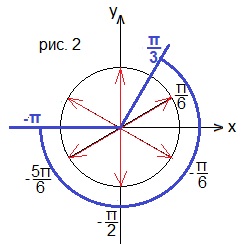
Все отмеченные углы рассмотрим на отрезке [-π; π/3]. Смотрим рисунок 2. Получились числа -5π/6; -π/2; -π/6; π/6.
Ответ: а) π/6+πn/3, где nϵZ; б) -5π/6; -π/2; -π/6; π/6.
Пример 2.
а) Решить уравнение cos4x-sin2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [0; π].
Решение.
а) Применим формулу 1-cos2α=2sin2α; тогда данное уравнение примет вид:
1-2sin22x-sin2x=0; 2sin22x+sin2x-1=0. Сделаем замену: sin2x=t.
Получаем равенство: 2t2+t-1=0.
У нас a-b+c=0, поэтому по методу коэффициентов t1=-1, t2=1/2.
- При sin2x=-1 получаем 2х=-π/2+2πn, отсюда х=-π/4+πn, где nϵZ.
- При sin2x=1/2 получаем 2х=π/6+2πn и 2х=5π/6+2πn, где nϵZ.
Тогда х=π/12+πn и х=5π/12+πn, где nϵZ.
Рассмотрим решения 2х=-π/2+2πn, 2х=π/6+2πn и 2х=5π/6+2πn на единичной окружности. Возьмём значения 2х при n=0. Углы -π/2, π/6 и 5π/6 отличаются друг от друга на значение 2π/3. Тогда общим решением будут являться числа
2х=π/6+(2π/3)n, отсюда общим решением данного уравнения будут
значения х=π/12+(π/3)n, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [0; π]. Для этого в общее решение х=π/12+(π/3)n, где nϵZ будем подставлять такие целые значения nϵZ,
чтобы хϵ[0; π].
Возьмём n=0, тогда х=π/12 ϵ[0; π].
При n=1 получим х= π/12+π/3= π/12+4π/12=5π/12 ϵ[0; π].
При n=2 получим х= π/12+2π/3= π/12+8π/12=9π/12=3π/4 ϵ[0; π].
При n=3 получим х= π/12+π, и это значение не входит в заданный отрезок [0; π].
Ответ: а) π/12+(π/3)n, где nϵZ; б) π/12, 5π/12, 3π/4.
Пример 3.
а) Решить уравнение
![]()
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Решение.
а) Применим формулу cos(α-β)=cosα∙cosβ+sinα∙sinβ; тогда данное уравнение примет вид:
cos3x=cos23x; cos23x-cos3x=0; cos3x(cos3x-1)=0;
cos3x=0 или cos3x-1=0.
- Если cos3x=0, то 3х=π/2+πn, тогда х= π/6+(π/3)n, где nϵZ.
- Если cos3x-1=0, то cos3x=1, тогда 3х=2πm, тогда х=(2π/3)m, где mϵZ.
Общие решения данного уравнения: х=π/6+(π/3)n, где nϵZ и х=(2π/3)m, где mϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Мы получили значения 3х=π/2+πn и 3х=2πm. Отметим их на единичной окружности, сделав замену 3х=t. Смотрите рисунок 3.
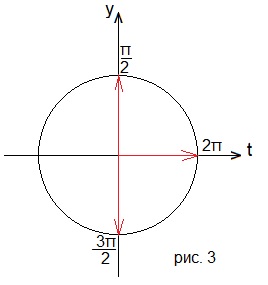
Необходимо выполнение условие хϵ[π; 3π/2]. Отсюда следует, что 3хϵ[3π; 9π/2].
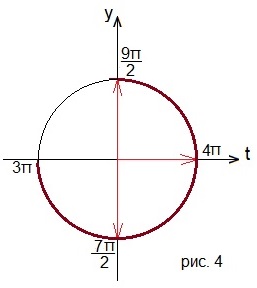
Все отмеченные углы рассмотрим на отрезке [3π; 9π/2]. Смотрим рисунок 4. Получились числа 7π/2; 4π; 9π/2. Так как это значения 3х, то делим каждое из них на 3. Получим: 7π/6; 4π/3; 3π/2.
Ответ: а) π/6+(π/3)n, где nϵZ; (2π/3)m, где mϵZ.
б) 7π/6; 4π/3; 3π/2.


