Высота цилиндра равна 3, а радиус основания равен 13
Задача. Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
Решение.
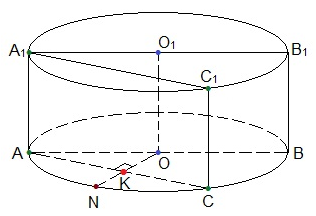 Плоскость сечения, параллельная основанию цилиндра представляет собой прямоугольник AA1C1C, площадь которого S = AC ∙ AA1.
Плоскость сечения, параллельная основанию цилиндра представляет собой прямоугольник AA1C1C, площадь которого S = AC ∙ AA1.
Так как по условию Sсеч. = 72
и АА1 = 3, то АС = 72 : 3 = 24.
Заметим, что хорда AC немногим меньше диаметра основания цилиндра (АВ = 2R = 2 ∙ 13 = 26).
Так как плоскость АА1С параллельна оси цилиндра ОО1, то расстояние до нее от точки О — длина перпендикуляра, проведенного из точки О к АС.
Проведем радиус ON перпендикулярно хорде AC.
Радиус, перпендикулярный хорде, делит ее и стягиваемую ею дугу пополам.
Точка K — середина AC, поэтому АК = АС : 2 = 24 : 2 = 12.
OK – искомый отрезок.
Рассмотрим прямоугольный треугольник АКО. По теореме Пифагора:
ОК2 = АО2 – АК2 = 132 – 122 =169 – 144 = 25, отсюда ОК = 5.
Это и есть расстояние от плоского сечения до центра основания цилиндра.
Ответ: 5.


